In this article, we will introduce a new variation of neural network which is the Recurrent Neural Network also known as (RNN) that works better than a simple neural network when data is sequential like Time-Series data and text data.
What is Recurrent Neural Network (RNN)?
Recurrent Neural Network(RNN) is a type of Neural Network where the output from the previous step is fed as input to the current step. In traditional neural networks, all the inputs and outputs are independent of each other. Still, in cases when it is required to predict the next word of a sentence, the previous words are required and hence there is a need to remember the previous words. Thus RNN came into existence, which solved this issue with the help of a Hidden Layer. The main and most important feature of RNN is its Hidden state, which remembers some information about a sequence. The state is also referred to as Memory State since it remembers the previous input to the network. It uses the same parameters for each input as it performs the same task on all the inputs or hidden layers to produce the output. This reduces the complexity of parameters, unlike other neural networks.

Recurrent Neural Network
How RNN differs from Feedforward Neural Network?
Artificial neural networks that do not have looping nodes are called feed forward neural networks. Because all information is only passed forward, this kind of neural network is also referred to as a multi-layer neural network.
Information moves from the input layer to the output layer – if any hidden layers are present – unidirectionally in a feedforward neural network. These networks are appropriate for image classification tasks, for example, where input and output are independent. Nevertheless, their inability to retain previous inputs automatically renders them less useful for sequential data analysis.
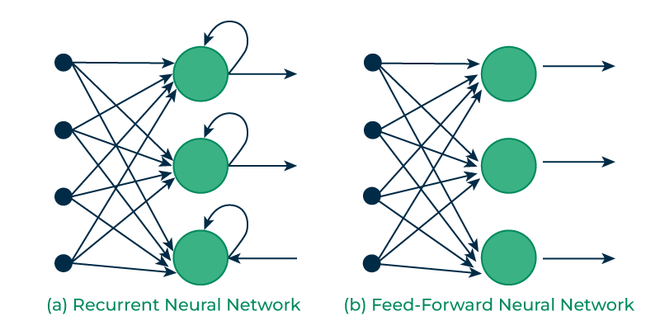
Recurrent Vs Feedfoward networks
Recurrent Neuron and RNN Unfolding
The fundamental processing unit in a Recurrent Neural Network (RNN) is a Recurrent Unit, which is not explicitly called a “Recurrent Neuron.” This unit has the unique ability to maintain a hidden state, allowing the network to capture sequential dependencies by remembering previous inputs while processing. Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) versions improve the RNN’s ability to handle long-term dependencies.
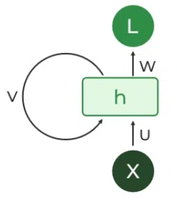
Recurrent Neuron

RNN Unfolding
Types Of RNN
There are four types of RNNs based on the number of inputs and outputs in the network.
- One to One
- One to Many
- Many to One
- Many to Many
One to One
This type of RNN behaves the same as any simple Neural network it is also known as Vanilla Neural Network. In this Neural network, there is only one input and one output.

One to One RNN
One To Many
In this type of RNN, there is one input and many outputs associated with it. One of the most used examples of this network is Image captioning where given an image we predict a sentence having Multiple words.
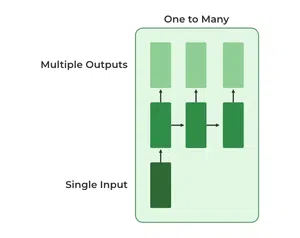
One to Many RNN
Many to One
In this type of network, Many inputs are fed to the network at several states of the network generating only one output. This type of network is used in the problems like sentimental analysis. Where we give multiple words as input and predict only the sentiment of the sentence as output.

Many to One RNN
Many to Many
In this type of neural network, there are multiple inputs and multiple outputs corresponding to a problem. One Example of this Problem will be language translation. In language translation, we provide multiple words from one language as input and predict multiple words from the second language as output.
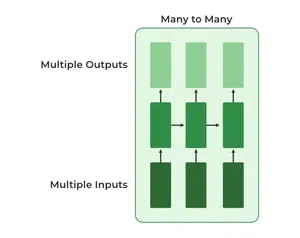
Many to Many RNN
Recurrent Neural Network Architecture
RNNs have the same input and output architecture as any other deep neural architecture. However, differences arise in the way information flows from input to output. Unlike Deep neural networks where we have different weight matrices for each Dense network in RNN, the weight across the network remains the same. It calculates state hidden state Hi for every input Xi . By using the following formulas:
h= σ(UX + Wh-1 + B)
Y = O(Vh + C)
Hence
Y = f (X, h , W, U, V, B, C)
Here S is the State matrix which has element si as the state of the network at timestep i
The parameters in the network are W, U, V, c, b which are shared across timestep

Recurrent Neural Architecture
How does RNN work?
The Recurrent Neural Network consists of multiple fixed activation function units, one for each time step. Each unit has an internal state which is called the hidden state of the unit. This hidden state signifies the past knowledge that the network currently holds at a given time step. This hidden state is updated at every time step to signify the change in the knowledge of the network about the past. The hidden state is updated using the following recurrence relation:-
The formula for calculating the current state:

where,
- ht -> current state
- ht-1 -> previous state
- xt -> input state
Formula for applying Activation function(tanh)

where,
- whh -> weight at recurrent neuron
- wxh -> weight at input neuron
The formula for calculating output:

- Yt -> output
- Why -> weight at output layer
These parameters are updated using Backpropagation. However, since RNN works on sequential data here we use an updated backpropagation which is known as Backpropagation through time.
Backpropagation Through Time (BPTT)
In RNN the neural network is in an ordered fashion and since in the ordered network each variable is computed one at a time in a specified order like first h1 then h2 then h3 so on. Hence we will apply backpropagation throughout all these hidden time states sequentially.
.webp)
Backpropagation Through Time (BPTT) In RNN
- L(θ)(loss function) depends on h3
- h3 in turn depends on h2 and W
- h2 in turn depends on h1 and W
- h1 in turn depends on h0 and W
- where h0 is a constant starting state.

For simplicity of this equation, we will apply backpropagation on only one row

We already know how to compute this one as it is the same as any simple deep neural network backpropagation.

.However, we will see how to apply backpropagation to this term 
As we know h3 = σ(Wh2 + b)
And In such an ordered network, we can’t compute  by simply treating h3 as a constant because as it also depends on W. the total derivative
by simply treating h3 as a constant because as it also depends on W. the total derivative  has two parts:
has two parts:
- Explicit:
 treating all other inputs as constant
treating all other inputs as constant - Implicit: Summing over all indirect paths from h3 to W
Let us see how to do this
![Rendered by QuickLaTeX.com \begin{aligned} \frac{\partial h_{3}}{\partial W} &=\frac{\partial h_{3}^{+}}{\partial W} +\frac{\partial h_{3}}{\partial h_{2}}\frac{\partial h_{2}}{\partial W} \\ &=\frac{\partial h_{3}^{+}}{\partial W} +\frac{\partial h_{3}}{\partial h_{2}} \left [\frac{\partial h_{2}^{+}}{\partial W} +\frac{\partial h_{2}}{\partial h_{1}}\frac{\partial h_{1}}{\partial W} \right ] \\ &=\frac{\partial h_{3}^{+}}{\partial W} +\frac{\partial h_{3}}{\partial h_{2}}\frac{\partial h_{2}^{+}}{\partial W} +\frac{\partial h_{3}}{\partial h_{2}}\frac{\partial h_{2}}{\partial h_{1}} \left [\frac{\partial h_{1}^{+}}{\partial W} \right ] \end{aligned}](https://quicklatex.com/cache3/ef/ql_725879304ba35362a5b698a67f500aef_l3.png)
For simplicity, we will short-circuit some of the paths

Finally, we have

Where

Hence,

This algorithm is called backpropagation through time (BPTT) as we backpropagate over all previous time steps
Issues of Standard RNNs
- Vanishing Gradient: Text generation, machine translation, and stock market prediction are just a few examples of the time-dependent and sequential data problems that can be modelled with recurrent neural networks. You will discover, though, that the gradient problem makes training RNN difficult.
- Exploding Gradient: An Exploding Gradient occurs when a neural network is being trained and the slope tends to grow exponentially rather than decay. Large error gradients that build up during training lead to very large updates to the neural network model weights, which is the source of this issue.
Training through RNN
- A single-time step of the input is provided to the network.
- Then calculate its current state using a set of current input and the previous state.
- The current ht becomes ht-1 for the next time step.
- One can go as many time steps according to the problem and join the information from all the previous states.
- Once all the time steps are completed the final current state is used to calculate the output.
- The output is then compared to the actual output i.e the target output and the error is generated.
- The error is then back-propagated to the network to update the weights and hence the network (RNN) is trained using Backpropagation through time.
Advantages and Disadvantages of Recurrent Neural Network
Advantages
- An RNN remembers each and every piece of information through time. It is useful in time series prediction only because of the feature to remember previous inputs as well. This is called Long Short Term Memory.
- Recurrent neural networks are even used with convolutional layers to extend the effective pixel neighborhood.
Disadvantages
- Gradient vanishing and exploding problems.
- Training an RNN is a very difficult task.
- It cannot process very long sequences if using tanh or relu as an activation function.
Applications of Recurrent Neural Network
- Language Modelling and Generating Text
- Speech Recognition
- Machine Translation
- Image Recognition, Face detection
- Time series Forecasting
Variation Of Recurrent Neural Network (RNN)
To overcome the problems like vanishing gradient and exploding gradient descent several new advanced versions of RNNs are formed some of these are as;
- Bidirectional Neural Network (BiNN)
- Long Short-Term Memory (LSTM)
Bidirectional Neural Network (BiNN)
A BiNN is a variation of a Recurrent Neural Network in which the input information flows in both direction and then the output of both direction are combined to produce the input. BiNN is useful in situations when the context of the input is more important such as Nlp tasks and Time-series analysis problems.
Long Short-Term Memory (LSTM)
Long Short-Term Memory works on the read-write-and-forget principle where given the input information network reads and writes the most useful information from the data and it forgets about the information which is not important in predicting the output. For doing this three new gates are introduced in the RNN. In this way, only the selected information is passed through the network.
Difference between RNN and Simple Neural Network
RNN is considered to be the better version of deep neural when the data is sequential. There are significant differences between the RNN and deep neural networks they are listed as:
| Recurrent Neural Network | Deep Neural Network |
| Weights are same across all the layers number of a Recurrent Neural Network | Weights are different for each layer of the network |
| Recurrent Neural Networks are used when the data is sequential and the number of inputs is not predefined. | A Simple Deep Neural network does not have any special method for sequential data also here the the number of inputs is fixed |
| The Numbers of parameter in the RNN are higher than in simple DNN | The Numbers of Parameter are lower than RNN |
| Exploding and vanishing gradients is the the major drawback of RNN | These problems also occur in DNN but these are not the major problem with DNN |
RNN Code Implementation
Imported libraries:
Imported some necessary libraries such as numpy, tensorflow for numerical calculation an model building.
Python3
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import SimpleRNN, Dense
|
Input Generation:
Generated some example data using text.
Python3
text = "This is GeeksforGeeks a software training institute"
chars = sorted(list(set(text)))
char_to_index = {char: i for i, char in enumerate(chars)}
index_to_char = {i: char for i, char in enumerate(chars)}
|
Created input sequences and corresponding labels for further implementation.
Python3
seq_length = 3
sequences = []
labels = []
for i in range(len(text) - seq_length):
seq = text[i:i+seq_length]
label = text[i+seq_length]
sequences.append([char_to_index[char] for char in seq])
labels.append(char_to_index[label])
|
Converted sequences and labels into numpy arrays and used one-hot encoding to convert text into vector.
Python3
X = np.array(sequences)
y = np.array(labels)
X_one_hot = tf.one_hot(X, len(chars))
y_one_hot = tf.one_hot(y, len(chars))
|
Model Building:
Build RNN Model using ‘relu’ and ‘softmax‘ activation function.
Python3
model = Sequential()
model.add(SimpleRNN(50, input_shape=(seq_length, len(chars)), activation='relu'))
model.add(Dense(len(chars), activation='softmax'))
|
Model Compilation:
The model.compile line builds the neural network for training by specifying the optimizer (Adam), the loss function (categorical crossentropy), and the training metric (accuracy).
Python3
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
|
Model Training:
Using the input sequences (X_one_hot) and corresponding labels (y_one_hot) for 100 epochs, the model is trained using the model.fit line, which optimises the model parameters to minimise the categorical crossentropy loss.
Python3
model.fit(X_one_hot, y_one_hot, epochs=100)
|
output:
Epoch 1/100
2/2 [==============================] - 2s 54ms/step - loss: 2.8327 - accuracy: 0.0000e+00
Epoch 2/100
2/2 [==============================] - 0s 16ms/step - loss: 2.8121 - accuracy: 0.0000e+00
Epoch 3/100
2/2 [==============================] - 0s 16ms/step - loss: 2.7944 - accuracy: 0.0208
Epoch 4/100
2/2 [==============================] - 0s 16ms/step - loss: 2.7766 - accuracy: 0.0208
Epoch 5/100
2/2 [==============================] - 0s 15ms/step - loss: 2.7596 - accuracy: 0.0625
Epoch 6/100
2/2 [==============================] - 0s 13ms/step - loss: 2.7424 - accuracy: 0.0833
Epoch 7/100
2/2 [==============================] - 0s 13ms/step - loss: 2.7254 - accuracy: 0.1042
Epoch 8/100
2/2 [==============================] - 0s 12ms/step - loss: 2.7092 - accuracy: 0.1042
Epoch 9/100
2/2 [==============================] - 0s 11ms/step - loss: 2.6917 - accuracy: 0.1458
Epoch 10/100
2/2 [==============================] - 0s 12ms/step - loss: 2.6742 - accuracy: 0.1667
Epoch 11/100
2/2 [==============================] - 0s 10ms/step - loss: 2.6555 - accuracy: 0.1667
Epoch 12/100
2/2 [==============================] - 0s 16ms/step - loss: 2.6369 - accuracy: 0.1667
Epoch 13/100
2/2 [==============================] - 0s 11ms/step - loss: 2.6179 - accuracy: 0.1667
Epoch 14/100
2/2 [==============================] - 0s 11ms/step - loss: 2.5993 - accuracy: 0.1875
Epoch 15/100
2/2 [==============================] - 0s 17ms/step - loss: 2.5789 - accuracy: 0.2083
Epoch 16/100
2/2 [==============================] - 0s 11ms/step - loss: 2.5593 - accuracy: 0.2083
Epoch 17/100
2/2 [==============================] - 0s 16ms/step - loss: 2.5397 - accuracy: 0.2083
Epoch 18/100
2/2 [==============================] - 0s 20ms/step - loss: 2.5182 - accuracy: 0.2292
Epoch 19/100
2/2 [==============================] - 0s 18ms/step - loss: 2.4979 - accuracy: 0.2292
Epoch 20/100
2/2 [==============================] - 0s 11ms/step - loss: 2.4761 - accuracy: 0.2292
Epoch 21/100
2/2 [==============================] - 0s 13ms/step - loss: 2.4536 - accuracy: 0.2292
Epoch 22/100
2/2 [==============================] - 0s 17ms/step - loss: 2.4299 - accuracy: 0.2292
Epoch 23/100
2/2 [==============================] - 0s 10ms/step - loss: 2.4067 - accuracy: 0.2708
Epoch 24/100
2/2 [==============================] - 0s 27ms/step - loss: 2.3824 - accuracy: 0.2917
Epoch 25/100
2/2 [==============================] - 0s 22ms/step - loss: 2.3582 - accuracy: 0.2917
Epoch 26/100
2/2 [==============================] - 0s 10ms/step - loss: 2.3324 - accuracy: 0.2917
Epoch 27/100
2/2 [==============================] - 0s 10ms/step - loss: 2.3068 - accuracy: 0.3125
Epoch 28/100
2/2 [==============================] - 0s 10ms/step - loss: 2.2819 - accuracy: 0.3125
Epoch 29/100
2/2 [==============================] - 0s 11ms/step - loss: 2.2535 - accuracy: 0.3333
Epoch 30/100
2/2 [==============================] - 0s 10ms/step - loss: 2.2278 - accuracy: 0.3333
Epoch 31/100
2/2 [==============================] - 0s 12ms/step - loss: 2.1992 - accuracy: 0.3333
Epoch 32/100
2/2 [==============================] - 0s 12ms/step - loss: 2.1719 - accuracy: 0.3333
Epoch 33/100
2/2 [==============================] - 0s 13ms/step - loss: 2.1434 - accuracy: 0.3333
Epoch 34/100
2/2 [==============================] - 0s 14ms/step - loss: 2.1134 - accuracy: 0.3542
Epoch 35/100
2/2 [==============================] - 0s 14ms/step - loss: 2.0852 - accuracy: 0.3542
Epoch 36/100
2/2 [==============================] - 0s 15ms/step - loss: 2.0547 - accuracy: 0.3958
Epoch 37/100
2/2 [==============================] - 0s 18ms/step - loss: 2.0240 - accuracy: 0.4167
Epoch 38/100
2/2 [==============================] - 0s 24ms/step - loss: 1.9933 - accuracy: 0.5000
Epoch 39/100
2/2 [==============================] - 0s 14ms/step - loss: 1.9626 - accuracy: 0.5000
Epoch 40/100
2/2 [==============================] - 0s 14ms/step - loss: 1.9306 - accuracy: 0.5000
Epoch 41/100
2/2 [==============================] - 0s 16ms/step - loss: 1.9002 - accuracy: 0.5000
Epoch 42/100
2/2 [==============================] - 0s 15ms/step - loss: 1.8669 - accuracy: 0.5000
Epoch 43/100
2/2 [==============================] - 0s 14ms/step - loss: 1.8353 - accuracy: 0.5208
Epoch 44/100
2/2 [==============================] - 0s 22ms/step - loss: 1.8029 - accuracy: 0.5417
Epoch 45/100
2/2 [==============================] - 0s 15ms/step - loss: 1.7708 - accuracy: 0.5625
Epoch 46/100
2/2 [==============================] - 0s 10ms/step - loss: 1.7373 - accuracy: 0.5625
Epoch 47/100
2/2 [==============================] - 0s 12ms/step - loss: 1.7052 - accuracy: 0.6042
Epoch 48/100
2/2 [==============================] - 0s 12ms/step - loss: 1.6737 - accuracy: 0.6042
Epoch 49/100
2/2 [==============================] - 0s 14ms/step - loss: 1.6388 - accuracy: 0.6250
Epoch 50/100
2/2 [==============================] - 0s 12ms/step - loss: 1.6071 - accuracy: 0.6458
Epoch 51/100
2/2 [==============================] - 0s 10ms/step - loss: 1.5737 - accuracy: 0.6667
Epoch 52/100
2/2 [==============================] - 0s 12ms/step - loss: 1.5386 - accuracy: 0.6667
Epoch 53/100
2/2 [==============================] - 0s 11ms/step - loss: 1.5059 - accuracy: 0.6875
Epoch 54/100
2/2 [==============================] - 0s 17ms/step - loss: 1.4727 - accuracy: 0.6875
Epoch 55/100
2/2 [==============================] - 0s 14ms/step - loss: 1.4381 - accuracy: 0.6667
Epoch 56/100
2/2 [==============================] - 0s 13ms/step - loss: 1.4039 - accuracy: 0.6667
Epoch 57/100
2/2 [==============================] - 0s 15ms/step - loss: 1.3718 - accuracy: 0.6667
Epoch 58/100
2/2 [==============================] - 0s 10ms/step - loss: 1.3391 - accuracy: 0.6667
Epoch 59/100
2/2 [==============================] - 0s 11ms/step - loss: 1.3059 - accuracy: 0.6875
Epoch 60/100
2/2 [==============================] - 0s 11ms/step - loss: 1.2751 - accuracy: 0.6875
Epoch 61/100
2/2 [==============================] - 0s 10ms/step - loss: 1.2426 - accuracy: 0.6875
Epoch 62/100
2/2 [==============================] - 0s 10ms/step - loss: 1.2123 - accuracy: 0.6875
Epoch 63/100
2/2 [==============================] - 0s 9ms/step - loss: 1.1822 - accuracy: 0.6875
Epoch 64/100
2/2 [==============================] - 0s 10ms/step - loss: 1.1520 - accuracy: 0.7083
Epoch 65/100
2/2 [==============================] - 0s 11ms/step - loss: 1.1232 - accuracy: 0.7500
Epoch 66/100
2/2 [==============================] - 0s 13ms/step - loss: 1.0940 - accuracy: 0.7500
Epoch 67/100
2/2 [==============================] - 0s 13ms/step - loss: 1.0677 - accuracy: 0.7500
Epoch 68/100
2/2 [==============================] - 0s 11ms/step - loss: 1.0388 - accuracy: 0.7500
Epoch 69/100
2/2 [==============================] - 0s 10ms/step - loss: 1.0130 - accuracy: 0.7500
Epoch 70/100
2/2 [==============================] - 0s 12ms/step - loss: 0.9862 - accuracy: 0.7917
Epoch 71/100
2/2 [==============================] - 0s 12ms/step - loss: 0.9619 - accuracy: 0.8125
Epoch 72/100
2/2 [==============================] - 0s 11ms/step - loss: 0.9377 - accuracy: 0.8333
Epoch 73/100
2/2 [==============================] - 0s 11ms/step - loss: 0.9114 - accuracy: 0.8542
Epoch 74/100
2/2 [==============================] - 0s 12ms/step - loss: 0.8882 - accuracy: 0.8542
Epoch 75/100
2/2 [==============================] - 0s 11ms/step - loss: 0.8656 - accuracy: 0.8750
Epoch 76/100
2/2 [==============================] - 0s 11ms/step - loss: 0.8423 - accuracy: 0.8750
Epoch 77/100
2/2 [==============================] - 0s 19ms/step - loss: 0.8214 - accuracy: 0.8750
Epoch 78/100
2/2 [==============================] - 0s 13ms/step - loss: 0.7991 - accuracy: 0.8750
Epoch 79/100
2/2 [==============================] - 0s 14ms/step - loss: 0.7781 - accuracy: 0.8750
Epoch 80/100
2/2 [==============================] - 0s 13ms/step - loss: 0.7568 - accuracy: 0.8750
Epoch 81/100
2/2 [==============================] - 0s 15ms/step - loss: 0.7386 - accuracy: 0.8750
Epoch 82/100
2/2 [==============================] - 0s 20ms/step - loss: 0.7178 - accuracy: 0.8750
Epoch 83/100
2/2 [==============================] - 0s 17ms/step - loss: 0.7001 - accuracy: 0.8750
Epoch 84/100
2/2 [==============================] - 0s 21ms/step - loss: 0.6814 - accuracy: 0.8750
Epoch 85/100
2/2 [==============================] - 0s 20ms/step - loss: 0.6641 - accuracy: 0.8750
Epoch 86/100
2/2 [==============================] - 0s 18ms/step - loss: 0.6464 - accuracy: 0.8750
Epoch 87/100
2/2 [==============================] - 0s 18ms/step - loss: 0.6290 - accuracy: 0.8750
Epoch 88/100
2/2 [==============================] - 0s 13ms/step - loss: 0.6108 - accuracy: 0.8750
Epoch 89/100
2/2 [==============================] - 0s 16ms/step - loss: 0.5958 - accuracy: 0.8750
Epoch 90/100
2/2 [==============================] - 0s 15ms/step - loss: 0.5799 - accuracy: 0.8750
Epoch 91/100
2/2 [==============================] - 0s 17ms/step - loss: 0.5656 - accuracy: 0.8750
Epoch 92/100
2/2 [==============================] - 0s 31ms/step - loss: 0.5499 - accuracy: 0.8750
Epoch 93/100
2/2 [==============================] - 0s 15ms/step - loss: 0.5347 - accuracy: 0.8750
Epoch 94/100
2/2 [==============================] - 0s 17ms/step - loss: 0.5215 - accuracy: 0.8750
Epoch 95/100
2/2 [==============================] - 0s 16ms/step - loss: 0.5077 - accuracy: 0.8958
Epoch 96/100
2/2 [==============================] - 0s 15ms/step - loss: 0.4954 - accuracy: 0.9583
Epoch 97/100
2/2 [==============================] - 0s 11ms/step - loss: 0.4835 - accuracy: 0.9583
Epoch 98/100
2/2 [==============================] - 0s 12ms/step - loss: 0.4715 - accuracy: 0.9583
Epoch 99/100
2/2 [==============================] - 0s 15ms/step - loss: 0.4588 - accuracy: 0.9583
Epoch 100/100
2/2 [==============================] - 0s 10ms/step - loss: 0.4469 - accuracy: 0.9583
<keras.src.callbacks.History at 0x7bab7ab127d0>
Model Prediction:
Generated text using pre-trained model.
Python3
start_seq = "This is G"
generated_text = start_seq
for i in range(50):
x = np.array([[char_to_index[char] for char in generated_text[-seq_length:]]])
x_one_hot = tf.one_hot(x, len(chars))
prediction = model.predict(x_one_hot)
next_index = np.argmax(prediction)
next_char = index_to_char[next_index]
generated_text += next_char
print("Generated Text:")
print(generated_text)
|
output:
1/1 [==============================] - 1s 517ms/step
1/1 [==============================] - 0s 75ms/step
1/1 [==============================] - 0s 101ms/step
1/1 [==============================] - 0s 93ms/step
1/1 [==============================] - 0s 132ms/step
1/1 [==============================] - 0s 143ms/step
1/1 [==============================] - 0s 140ms/step
1/1 [==============================] - 0s 144ms/step
1/1 [==============================] - 0s 125ms/step
1/1 [==============================] - 0s 60ms/step
1/1 [==============================] - 0s 38ms/step
1/1 [==============================] - 0s 34ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 34ms/step
1/1 [==============================] - 0s 32ms/step
1/1 [==============================] - 0s 32ms/step
1/1 [==============================] - 0s 38ms/step
1/1 [==============================] - 0s 32ms/step
1/1 [==============================] - 0s 36ms/step
1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 32ms/step
1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 23ms/step
1/1 [==============================] - 0s 27ms/step
1/1 [==============================] - 0s 21ms/step
1/1 [==============================] - 0s 23ms/step
1/1 [==============================] - 0s 20ms/step
1/1 [==============================] - 0s 20ms/step
1/1 [==============================] - 0s 22ms/step
1/1 [==============================] - 0s 24ms/step
1/1 [==============================] - 0s 21ms/step
1/1 [==============================] - 0s 22ms/step
1/1 [==============================] - 0s 21ms/step
1/1 [==============================] - 0s 23ms/step
1/1 [==============================] - 0s 24ms/step
1/1 [==============================] - 0s 23ms/step
1/1 [==============================] - 0s 22ms/step
1/1 [==============================] - 0s 22ms/step
1/1 [==============================] - 0s 23ms/step
1/1 [==============================] - 0s 21ms/step
1/1 [==============================] - 0s 22ms/step
1/1 [==============================] - 0s 25ms/step
1/1 [==============================] - 0s 24ms/step
1/1 [==============================] - 0s 21ms/step
1/1 [==============================] - 0s 21ms/step
1/1 [==============================] - 0s 20ms/step
1/1 [==============================] - 0s 20ms/step
Generated Text:
This is Geeks a software training instituteais is is is is
Frequently Asked Questions (FAQs):
Q. 1 What is RNN?
Ans. Recurrent neural networks (RNNs) are a type of artificial neural network that are primarily utilised in NLP (natural language processing) and speech recognition. RNN is utilised in deep learning and in the creation of models that simulate neuronal activity in the human brain.
Q. 2 Which type of problem can solved by RNN?
Ans. Modelling time-dependent and sequential data problems, like text generation, machine translation, and stock market prediction, is possible with recurrent neural networks. Nevertheless, you will discover that the gradient problem makes RNN difficult to train. The vanishing gradients issue affects RNNs.
Q. 3 What are the types of RNN?
Ans. There are four types of RNN are:
- One to One
- One to Many
- Many to One
- Many to Many
Q. 4 What is the differences between RNN and CNN?
Ans. The following are the key distinctions between CNNs and RNNs: CNNs are frequently employed in the solution of problems involving spatial data, like images. Text and video data that is temporally and sequentially organised is better analysed by RNNs. RNNs and CNNs are not designed alike.
Share your thoughts in the comments
Please Login to comment...