Difference Between Graph and Tree
Last Updated :
20 Mar, 2024
Graphs and trees are two fundamental data structures used in computer science to represent relationships between objects. While they share some similarities, they also have distinct differences that make them suitable for different applications.
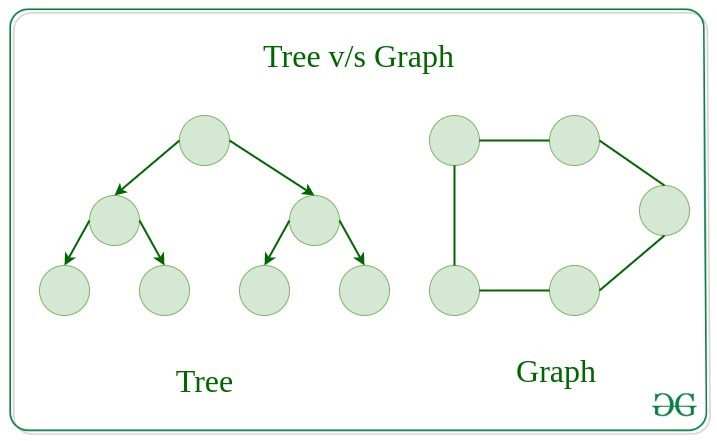
Difference Between Graph and Tree
A graph data structure is a collection of nodes (also called vertices) and edges that connect them. Nodes can represent entities, such as people, places, or things, while edges represent relationships between those entities.
Graphs are used to model a wide variety of real-world systems, such as social networks, transportation networks, and computer networks.
A tree data structure is a hierarchical data structure that consists of nodes connected by edges. Each node can have multiple child nodes, but only one parent node. The topmost node in the tree is called the root node.
Trees are often used to represent hierarchical data, such as file systems, XML documents, and organizational charts.
Difference Between Graph and Tree
| Feature |
Graph |
Tree |
| Definition |
A collection of nodes (vertices) and edges, where edges connect nodes. |
A hierarchical data structure consisting of nodes connected by edges with a single root node. |
| Structure |
Can have cycles (loops) and disconnected components. |
No cycles; connected structure with exactly one path between any two nodes. |
| Root Node |
No root node; nodes may have multiple parents or no parents at all. |
Has a designated root node that has no parent. |
| Node Relationship |
Relationships between nodes are arbitrary. |
Parent-child relationship; each node (except the root) has exactly one parent. |
| Edges |
Each node can have any number of edges. |
If there is n nodes then there would be n-1 number of edges |
| Traversal Complexity |
Traversal can be complex due to cycles and disconnected components. |
Traversal is straightforward and can be done in linear time. |
| Application |
Used in various scenarios like social networks, maps, network optimization, etc. |
Commonly used for hierarchical data representation like file systems, organization charts, HTML DOM, XML documents, etc. |
| Examples |
Social networks, road networks, computer networks. |
File systems, family trees, HTML DOM structure. |
Key Differences Between Graph and Tree
- Cycles: Graphs can contain cycles, while trees cannot.
- Connectivity: Graphs can be disconnected (i.e., have multiple components), while trees are always connected.
- Hierarchy: Trees have a hierarchical structure, with one vertex designated as the root. Graphs do not have this hierarchical structure.
- Applications: Graphs are used in a wide variety of applications, such as social networks, transportation networks, and computer science. Trees are often used in hierarchical data structures, such as file systems and XML documents.
Share your thoughts in the comments
Please Login to comment...