Introduction to Tree – Data Structure and Algorithm Tutorials
Last Updated :
24 Apr, 2024
Tree data structure is a specialized data structure to store data in hierarchical manner. It is used to organize and store data in the computer to be used more effectively. It consists of a central node, structural nodes, and sub-nodes, which are connected via edges. We can also say that tree data structure has roots, branches, and leaves connected.
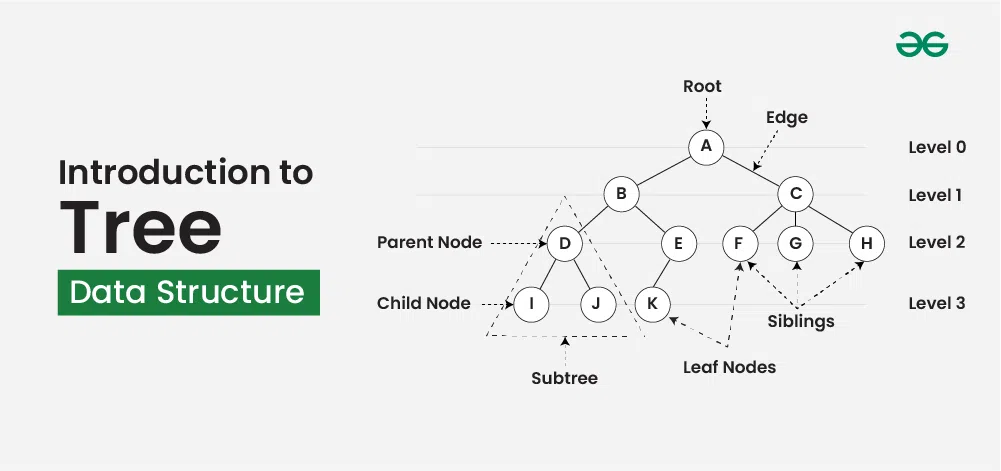
What is Tree Data Structure?
Tree data structure is a hierarchical structure that is used to represent and organize data in a way that is easy to navigate and search. It is a collection of nodes that are connected by edges and has a hierarchical relationship between the nodes.
The topmost node of the tree is called the root, and the nodes below it are called the child nodes. Each node can have multiple child nodes, and these child nodes can also have their own child nodes, forming a recursive structure.
Why Tree is considered a non-linear data structure?
The data in a tree are not stored in a sequential manner i.e., they are not stored linearly. Instead, they are arranged on multiple levels or we can say it is a hierarchical structure. For this reason, the tree is considered to be a non-linear data structure.
Basic Terminologies In Tree Data Structure:
- Parent Node: The node which is a predecessor of a node is called the parent node of that node. {B} is the parent node of {D, E}.
- Child Node: The node which is the immediate successor of a node is called the child node of that node. Examples: {D, E} are the child nodes of {B}.
- Root Node: The topmost node of a tree or the node which does not have any parent node is called the root node. {A} is the root node of the tree. A non-empty tree must contain exactly one root node and exactly one path from the root to all other nodes of the tree.
- Leaf Node or External Node: The nodes which do not have any child nodes are called leaf nodes. {K, L, M, N, O, P, G} are the leaf nodes of the tree.
- Ancestor of a Node: Any predecessor nodes on the path of the root to that node are called Ancestors of that node. {A,B} are the ancestor nodes of the node {E}
- Descendant: A node x is a descendant of another node y if and only if y is an ancestor of x.
- Sibling: Children of the same parent node are called siblings. {D,E} are called siblings.
- Level of a node: The count of edges on the path from the root node to that node. The root node has level 0.
- Internal node: A node with at least one child is called Internal Node.
- Neighbour of a Node: Parent or child nodes of that node are called neighbors of that node.
- Subtree: Any node of the tree along with its descendant.
Representation of Tree Data Structure:
A tree consists of a root node, and zero or more subtrees T1, T2, … , Tk such that there is an edge from the root node of the tree to the root node of each subtree. Subtree of a node X consists of all the nodes which have node X as the ancestor node.
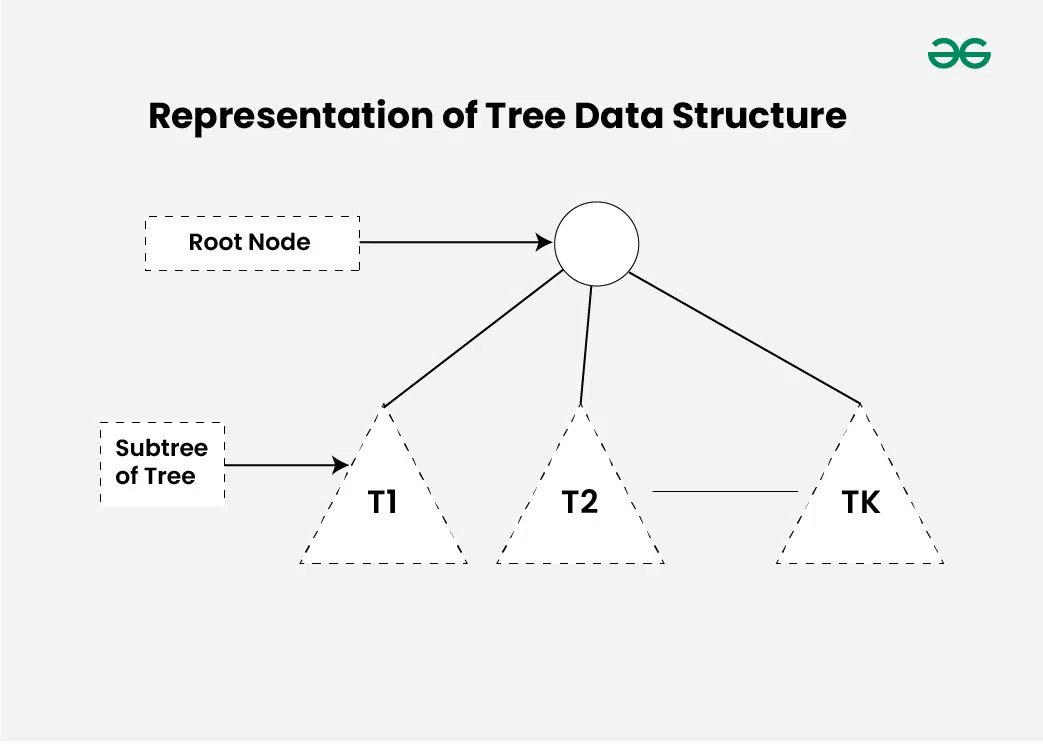
Representation of Tree Data Structure
Representation of a Node in Tree Data Structure:
A tree can be represented using a collection of nodes. Each of the nodes can be represented with the help of class or structs. Below is the representation of Node in different languages:
C++
class Node {
public:
int data;
Node* first_child;
Node* second_child;
Node* third_child;
.
.
.
Node* nth_child;
};
struct Node {
int data;
struct Node* first_child;
struct Node* second_child;
struct Node* third_child;
.
.
.
struct Node* nth_child;
};
public static class Node {
int data;
Node first_child;
Node second_child;
Node third_child;
.
.
.
Node nth_child;
}
class Node:
def __init__(self, data):
self.data = data
self.children = []
class Node {
constructor(data) {
this.data = data;
this.children = [];
}
}
Importance for Tree Data Structure:
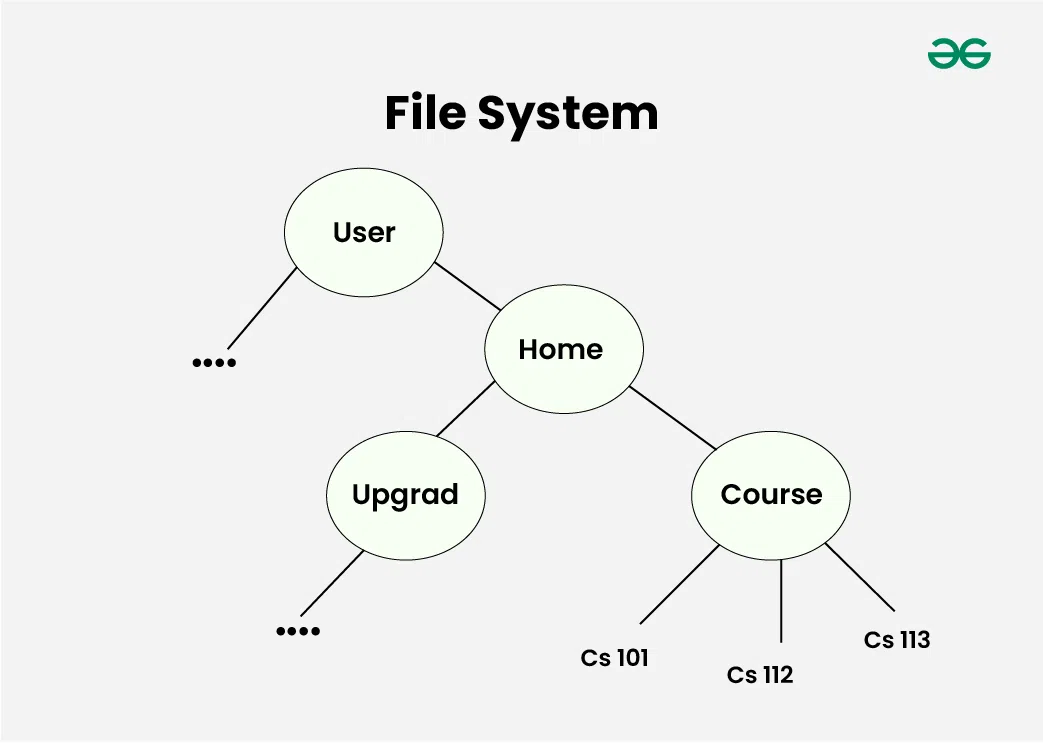
1. One reason to use trees might be because you want to store information that naturally forms a hierarchy. For example, the file system on a computer:
2. Trees (with some ordering e.g., BST) provide moderate access/search (quicker than Linked List and slower than arrays).
3. Trees provide moderate insertion/deletion (quicker than Arrays and slower than Unordered Linked Lists).
4. Like Linked Lists and unlike Arrays, Trees don’t have an upper limit on the number of nodes as nodes are linked using pointers.
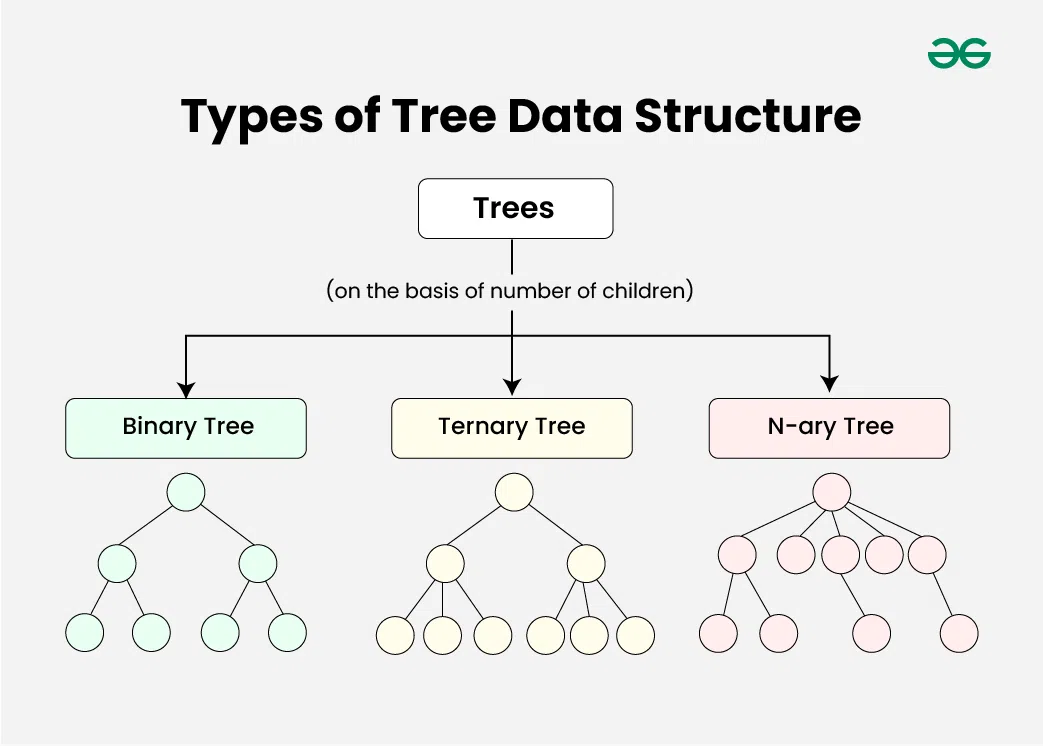
Tree data structure can be classified into three types based upon the number of children each node of the tree can have. The types are:
- Binary tree: In a binary tree, each node can have a maximum of two children linked to it. Some common types of binary trees include full binary trees, complete binary trees, balanced binary trees, and degenerate or pathological binary trees.
- Ternary Tree: A Ternary Tree is a tree data structure in which each node has at most three child nodes, usually distinguished as “left”, “mid” and “right”.
- N-ary Tree or Generic Tree: Generic trees are a collection of nodes where each node is a data structure that consists of records and a list of references to its children(duplicate references are not allowed). Unlike the linked list, each node stores the address of multiple nodes.
Basic Operations Of Tree Data Structure:
- Create – create a tree in the data structure.
- Insert − Inserts data in a tree.
- Search − Searches specific data in a tree to check whether it is present or not.
- Traversal:
Implementation of Tree Data Structure:
C++
// C++ program to demonstrate some of the above
// terminologies
#include <bits/stdc++.h>
using namespace std;
// Function to add an edge between vertices x and y
void addEdge(int x, int y, vector<vector<int> >& adj)
{
adj[x].push_back(y);
adj[y].push_back(x);
}
// Function to print the parent of each node
void printParents(int node, vector<vector<int> >& adj,
int parent)
{
// current node is Root, thus, has no parent
if (parent == 0)
cout << node << "->Root" << endl;
else
cout << node << "->" << parent << endl;
// Using DFS
for (auto cur : adj[node])
if (cur != parent)
printParents(cur, adj, node);
}
// Function to print the children of each node
void printChildren(int Root, vector<vector<int> >& adj)
{
// Queue for the BFS
queue<int> q;
// pushing the root
q.push(Root);
// visit array to keep track of nodes that have been
// visited
int vis[adj.size()] = { 0 };
// BFS
while (!q.empty()) {
int node = q.front();
q.pop();
vis[node] = 1;
cout << node << "-> ";
for (auto cur : adj[node])
if (vis[cur] == 0) {
cout << cur << " ";
q.push(cur);
}
cout << endl;
}
}
// Function to print the leaf nodes
void printLeafNodes(int Root, vector<vector<int> >& adj)
{
// Leaf nodes have only one edge and are not the root
for (int i = 1; i < adj.size(); i++)
if (adj[i].size() == 1 && i != Root)
cout << i << " ";
cout << endl;
}
// Function to print the degrees of each node
void printDegrees(int Root, vector<vector<int> >& adj)
{
for (int i = 1; i < adj.size(); i++) {
cout << i << ": ";
// Root has no parent, thus, its degree is equal to
// the edges it is connected to
if (i == Root)
cout << adj[i].size() << endl;
else
cout << adj[i].size() - 1 << endl;
}
}
// Driver code
int main()
{
// Number of nodes
int N = 7, Root = 1;
// Adjacency list to store the tree
vector<vector<int> > adj(N + 1, vector<int>());
// Creating the tree
addEdge(1, 2, adj);
addEdge(1, 3, adj);
addEdge(1, 4, adj);
addEdge(2, 5, adj);
addEdge(2, 6, adj);
addEdge(4, 7, adj);
// Printing the parents of each node
cout << "The parents of each node are:" << endl;
printParents(Root, adj, 0);
// Printing the children of each node
cout << "The children of each node are:" << endl;
printChildren(Root, adj);
// Printing the leaf nodes in the tree
cout << "The leaf nodes of the tree are:" << endl;
printLeafNodes(Root, adj);
// Printing the degrees of each node
cout << "The degrees of each node are:" << endl;
printDegrees(Root, adj);
return 0;
}
// java code for above approach
import java.io.*;
import java.util.*;
class GFG {
// Function to print the parent of each node
public static void
printParents(int node, Vector<Vector<Integer> > adj,
int parent)
{
// current node is Root, thus, has no parent
if (parent == 0)
System.out.println(node + "->Root");
else
System.out.println(node + "->" + parent);
// Using DFS
for (int i = 0; i < adj.get(node).size(); i++)
if (adj.get(node).get(i) != parent)
printParents(adj.get(node).get(i), adj,
node);
}
// Function to print the children of each node
public static void
printChildren(int Root, Vector<Vector<Integer> > adj)
{
// Queue for the BFS
Queue<Integer> q = new LinkedList<>();
// pushing the root
q.add(Root);
// visit array to keep track of nodes that have been
// visited
int vis[] = new int[adj.size()];
Arrays.fill(vis, 0);
// BFS
while (q.size() != 0) {
int node = q.peek();
q.remove();
vis[node] = 1;
System.out.print(node + "-> ");
for (int i = 0; i < adj.get(node).size(); i++) {
if (vis[adj.get(node).get(i)] == 0) {
System.out.print(adj.get(node).get(i)
+ " ");
q.add(adj.get(node).get(i));
}
}
System.out.println();
}
}
// Function to print the leaf nodes
public static void
printLeafNodes(int Root, Vector<Vector<Integer> > adj)
{
// Leaf nodes have only one edge and are not the
// root
for (int i = 1; i < adj.size(); i++)
if (adj.get(i).size() == 1 && i != Root)
System.out.print(i + " ");
System.out.println();
}
// Function to print the degrees of each node
public static void
printDegrees(int Root, Vector<Vector<Integer> > adj)
{
for (int i = 1; i < adj.size(); i++) {
System.out.print(i + ": ");
// Root has no parent, thus, its degree is
// equal to the edges it is connected to
if (i == Root)
System.out.println(adj.get(i).size());
else
System.out.println(adj.get(i).size() - 1);
}
}
// Driver code
public static void main(String[] args)
{
// Number of nodes
int N = 7, Root = 1;
// Adjacency list to store the tree
Vector<Vector<Integer> > adj
= new Vector<Vector<Integer> >();
for (int i = 0; i < N + 1; i++) {
adj.add(new Vector<Integer>());
}
// Creating the tree
adj.get(1).add(2);
adj.get(2).add(1);
adj.get(1).add(3);
adj.get(3).add(1);
adj.get(1).add(4);
adj.get(4).add(1);
adj.get(2).add(5);
adj.get(5).add(2);
adj.get(2).add(6);
adj.get(6).add(2);
adj.get(4).add(7);
adj.get(7).add(4);
// Printing the parents of each node
System.out.println("The parents of each node are:");
printParents(Root, adj, 0);
// Printing the children of each node
System.out.println(
"The children of each node are:");
printChildren(Root, adj);
// Printing the leaf nodes in the tree
System.out.println(
"The leaf nodes of the tree are:");
printLeafNodes(Root, adj);
// Printing the degrees of each node
System.out.println("The degrees of each node are:");
printDegrees(Root, adj);
}
}
// This code is contributed by rj13to.
from collections import deque
# Function to add an edge between vertices x and y
def addEdge(x, y, adj):
adj[x].append(y)
adj[y].append(x)
# Function to print the parent of each node
def printParents(node, adj, parent):
# current node is Root, thus, has no parent
if parent == 0:
print("{}->Root".format(node))
else:
print("{}->{}".format(node, parent))
# Using DFS
for cur in adj[node]:
if cur != parent:
printParents(cur, adj, node)
# Function to print the children of each node
def printChildren(Root, adj):
# Queue for the BFS
q = deque()
# pushing the root
q.append(Root)
# visit array to keep track of nodes that have been
# visited
vis = [0] * len(adj)
# BFS
while q:
node = q.popleft()
vis[node] = 1
print("{}->".format(node)),
for cur in adj[node]:
if vis[cur] == 0:
print(cur),
q.append(cur)
print()
# Function to print the leaf nodes
def printLeafNodes(Root, adj):
# Leaf nodes have only one edge and are not the root
for i in range(1, len(adj)):
if len(adj[i]) == 1 and i != Root:
print(i),
# Function to print the degrees of each node
def printDegrees(Root, adj):
for i in range(1, len(adj)):
print(i, ":"),
# Root has no parent, thus, its degree is equal to
# the edges it is connected to
if i == Root:
print(len(adj[i]))
else:
print(len(adj[i]) - 1)
# Driver code
N = 7
Root = 1
# Adjacency list to store the tree
adj = [[] for _ in range(N + 1)]
# Creating the tree
addEdge(1, 2, adj)
addEdge(1, 3, adj)
addEdge(1, 4, adj)
addEdge(2, 5, adj)
addEdge(2, 6, adj)
addEdge(4, 7, adj)
# Printing the parents of each node
print("The parents of each node are:")
printParents(Root, adj, 0)
# Printing the children of each node
print("The children of each node are:")
printChildren(Root, adj)
# Printing the leaf nodes in the tree
print("The leaf nodes of the tree are:")
printLeafNodes(Root, adj)
# Printing the degrees of each node
print("The degrees of each node are:")
printDegrees(Root, adj)
using System;
using System.Collections.Generic;
class Program
{
static void PrintParents(int node, List<List<int>> adj, int parent)
{
if (parent == 0)
{
Console.WriteLine($"{node} -> Root");
}
else
{
Console.WriteLine($"{node} -> {parent}");
}
foreach (int cur in adj[node])
{
if (cur != parent)
{
PrintParents(cur, adj, node);
}
}
}
static void PrintChildren(int Root, List<List<int>> adj)
{
Queue<int> q = new Queue<int>();
q.Enqueue(Root);
bool[] vis = new bool[adj.Count];
while (q.Count > 0)
{
int node = q.Dequeue();
vis[node] = true;
Console.Write($"{node} -> ");
foreach (int cur in adj[node])
{
if (!vis[cur])
{
Console.Write($"{cur} ");
q.Enqueue(cur);
}
}
Console.WriteLine();
}
}
static void PrintLeafNodes(int Root, List<List<int>> adj)
{
for (int i = 0; i < adj.Count; i++)
{
if (adj[i].Count == 1 && i != Root)
{
Console.Write($"{i} ");
}
}
Console.WriteLine();
}
static void PrintDegrees(int Root, List<List<int>> adj)
{
for (int i = 1; i < adj.Count; i++)
{
Console.Write($"{i}: ");
if (i == Root)
{
Console.WriteLine(adj[i].Count);
}
else
{
Console.WriteLine(adj[i].Count - 1);
}
}
}
static void Main(string[] args)
{
int N = 7;
int Root = 1;
List<List<int>> adj = new List<List<int>>();
for (int i = 0; i <= N; i++)
{
adj.Add(new List<int>());
}
adj[1].AddRange(new int[] { 2, 3, 4 });
adj[2].AddRange(new int[] { 1, 5, 6 });
adj[4].Add(7);
Console.WriteLine("The parents of each node are:");
PrintParents(Root, adj, 0);
Console.WriteLine("The children of each node are:");
PrintChildren(Root, adj);
Console.WriteLine("The leaf nodes of the tree are:");
PrintLeafNodes(Root, adj);
Console.WriteLine("The degrees of each node are:");
PrintDegrees(Root, adj);
}
}
// Number of nodes
let N = 7, Root = 1;
// Adjacency list to store the tree
let adj = new Array(N + 1).fill(null).map(() => []);
// Creating the tree
addEdge(1, 2, adj);
addEdge(1, 3, adj);
addEdge(1, 4, adj);
addEdge(2, 5, adj);
addEdge(2, 6, adj);
addEdge(4, 7, adj);
// Function to add an edge between vertices x and y
function addEdge(x, y, arr) {
arr[x].push(y);
arr[y].push(x);
}
// Function to print the parent of each node
function printParents(node, arr, parent)
{
// current node is Root, thus, has no parent
if (parent == 0)
console.log(`${node}->Root`);
else
console.log(`${node}->${parent}`);
// Using DFS
for (let cur of arr[node])
if (cur != parent)
printParents(cur, arr, node);
}
// Function to print the children of each node
function printChildren(Root, arr)
{
// Queue for the BFS
let q = [];
// pushing the root
q.push(Root);
// visit array to keep track of nodes that have been
// visited
let vis = new Array(arr.length).fill(0);
// BFS
while (q.length > 0) {
let node = q.shift();
vis[node] = 1;
console.log(`${node}-> `);
for (let cur of arr[node])
if (vis[cur] == 0) {
console.log(cur + " ");
q.push(cur);
}
console.log("\n");
}
}
// Function to print the leaf nodes
function printLeafNodes(Root, arr)
{
// Leaf nodes have only one edge and are not the root
for (let i = 1; i < arr.length; i++)
if (arr[i].length == 1 && i != Root)
console.log(i + " ");
console.log("\n");
}
// Function to print the degrees of each node
function printDegrees(Root, arr) {
for (let i = 1; i < arr.length; i++) {
console.log(`${i}: `);
// Root has no parent, thus, its degree is equal to
// the edges it is connected to
if (i == Root)
console.log(arr[i].length + "\n");
else
console.log(arr[i].length - 1 + "\n");
}
}
// Driver code
// Printing the parents of each node
console.log("The parents of each node are:");
printParents(Root, adj, 0);
// Printing the children of each node
console.log("The children of each node are:");
printChildren(Root, adj);
// Printing the leaf nodes in the tree
console.log("The leaf nodes of the tree are:");
printLeafNodes(Root, adj);
// Printing the degrees of each node
console.log("The degrees of each node are:");
printDegrees(Root, adj);
// This code is contributed by ruchikabaslas.
OutputThe parents of each node are:
1->Root
2->1
5->2
6->2
3->1
4->1
7->4
The children of each node are:
1-> 2 3 4
2-> 5 6
3->
4-> 7
5->
6->
7->
The leaf nodes of the tree are:
3 5 6 7
The degrees o...
Properties of Tree Data Structure:
- Number of edges: An edge can be defined as the connection between two nodes. If a tree has N nodes then it will have (N-1) edges. There is only one path from each node to any other node of the tree.
- Depth of a node: The depth of a node is defined as the length of the path from the root to that node. Each edge adds 1 unit of length to the path. So, it can also be defined as the number of edges in the path from the root of the tree to the node.
- Height of a node: The height of a node can be defined as the length of the longest path from the node to a leaf node of the tree.
- Height of the Tree: The height of a tree is the length of the longest path from the root of the tree to a leaf node of the tree.
- Degree of a Node: The total count of subtrees attached to that node is called the degree of the node. The degree of a leaf node must be 0. The degree of a tree is the maximum degree of a node among all the nodes in the tree.
- File System: This allows for efficient navigation and organization of files.
- Data Compression: Huffman coding is a popular technique for data compression that involves constructing a binary tree where the leaves represent characters and their frequency of occurrence. The resulting tree is used to encode the data in a way that minimizes the amount of storage required.
- Compiler Design: In compiler design, a syntax tree is used to represent the structure of a program.
- Database Indexing: B-trees and other tree structures are used in database indexing to efficiently search for and retrieve data.
- Tree offer Efficient Searching Depending on the type of tree, with average search times of O(log n) for balanced trees like AVL.
- Trees provide a hierarchical representation of data, making it easy to organize and navigate large amounts of information.
- The recursive nature of trees makes them easy to traverse and manipulate using recursive algorithms.
- Unbalanced Trees, meaning that the height of the tree is skewed towards one side, which can lead to inefficient search times.
- Trees demand more memory space requirements than some other data structures like arrays and linked lists, especially if the tree is very large.
- The implementation and manipulation of trees can be complex and require a good understanding of the algorithms.
Share your thoughts in the comments
Please Login to comment...