Division of Line Segment in Given Ratio – Constructions | Class 10 Maths
Last Updated :
05 Nov, 2020
Line is a straight one-dimensional figure that has no thickness. In geometry, a line extends endlessly in both directions. It is described as the shortest distance between any two points. A-line can also be understood as multiple points connected to each other in one specific direction without a gap between them.
Line Segment is a part of a line that is bounded by two different endpoints and contains every point on the line between its endpoints in the shortest possible distance.
Rules to write down the coordinates of the point which divides the join of two given points P(x1,y1) and Q(x2,y2) internally in a given ratio m1:m2
- Draw the line segment joining the given points P and Q
- Write down the coordinates of p and Q at extremities
- Let R(x, y) be the input which divides PQ internally in the ratio m1:m2
- For x-coordinate of R, multiply x2 with m1 and x1 with m2 and add the products. Divide the sum by m1+m2
- For y-coordinate of R, multiply y2 with m1 and y1 with m2 and add the products. Divide the sum by m1+m2
Derivation of Formula
Let P(x1, y1) and Q(x2, y2) be the two ends of a given line in a coordinate plane, and R(x,y) be the point on that line which divides PQ in the ratio m1:m2 such that
PR/RQ=m1/m2 …(1)
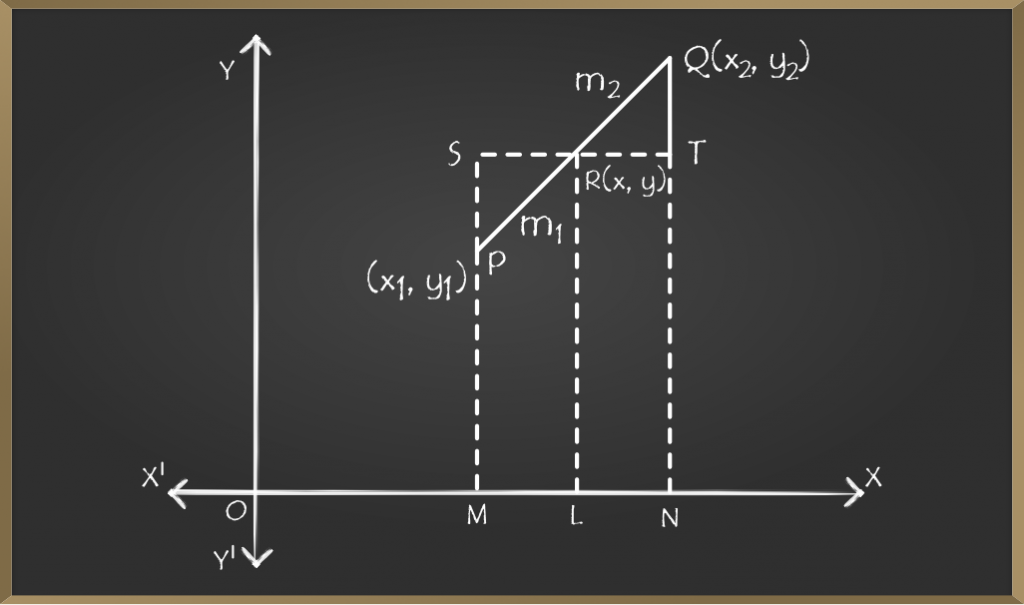
Drawing lines PM, QN, and RL perpendicular on the x-axis and through R draw a straight line parallel to the x-axis to meet MP at S and NQ at T.
Hence, from the figure, we can say,
SR = ML = OL – OM = x – x1 …(2)
RT = LN = ON – Ol = x2 – x …(3)
PS = MS – MP = LR – MP = y – y1 …(4)
TQ = NQ – NT = NQ – LR = y2 – y …(5)
Now ∆SPR is similar to ∆TQR
SR / RT = PR / RQ
By using equation 2, 3, and 1, we know,
x – x1 / x2 – x = m1 / m2
m2x – m2x1 = m1x2 – m1x
m1x + m2x = m1x2 + m2x1
(m1 + m2)x = m1x2 + m2x1
x = (m1x2 + m2x1) / (m1 + m2)
Now ∆SPR is similar to ∆TQR,
Therefore,
PS/TQ = PR/RQ
By using equation 4, 5, and 1, we know,
y – y1 / y2 – y = m1/m2
m2y – m2y1 = m1y2 – m1y
m1y + m2y = m1y2 + m2y1
(m1 + m2)y = m1y2 + m2y1
y = (m1y2 + m2y1)/(m1 + m2)
Hence, the coordinate of R(x,y) are,
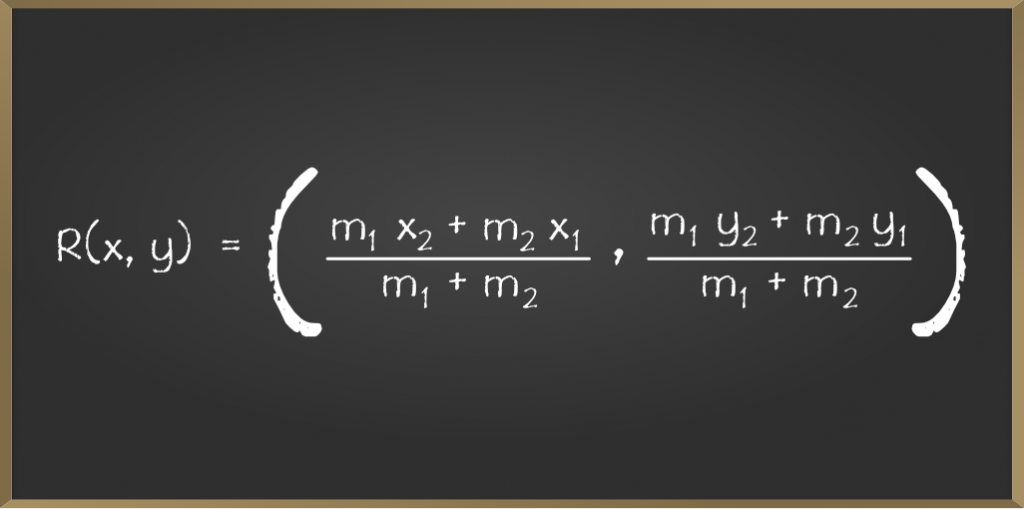
Sample Problems based on the Formula
Problem 1: Calculate the co-ordinates of the point P which divides the line joining A(-3,3) and B(2,-7) in the ratio 2:3
Solution:
Let (x, y) be th co-ordinates of the point P which divides the line joining A(-3, 3) and B(2, -7) in the ratio 2:3, then
Applying the formulae,
x = (m1x2 + m2x1) / (m1 + m2)
x = {2 x 2 + 3 x (-3)} / (2 + 3)
x = (4 – 9) / 5
x = -5 / 5
x = -1
y = (m1y2 + m2y1) / (m1 + m2)
y = {2 x (-7) + 3 x 3} / (2 + 3)
y = (-14 + 9) / 5
y = -5 / 5
y = -1
Hence the co-ordinates of point P are (-1, -1).
Problem 2: If the line joining the points A(4,-5) and B(4,5) is divided by point P such that AP/AB=2/5, find the coordinates of P.
Solution:
Given AP/AB = 2/5
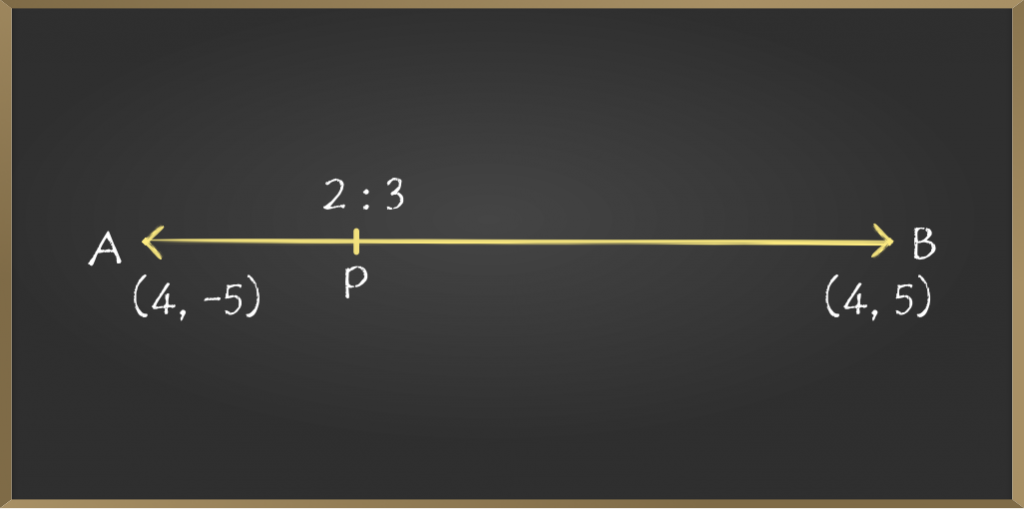
5AP = 2AB = 2(AP + PB)
3AP = 2PB
AP/PB = 2/3
AP:PB = 2:3
Thus the point P divides the line segment joining the points A(4, -5) and B(4, 5) in the ratio 2:3 internally.
Hence the coordinates of P are,
Px = (2 x 4 + 3 x 4)/(2 + 3)
= (8 + 12)/5
= 20/5
= 4
Py = (2 x 5 + 3 x (-5))/(2 + 3)
= (10 – 15)/5
= -5/5
= -1
Coordinates of P are (4, -1).
Problem 3: In what ratio does the point P(2, -5) divide the line segment joining the points A(-3, 5) and B(4, -9).
Solution:
Let P(2, -5) divide the line segment joining the points A(-3, 3) and B(4, -9) in the ratio k:1, i.e. AP:PB = k:1
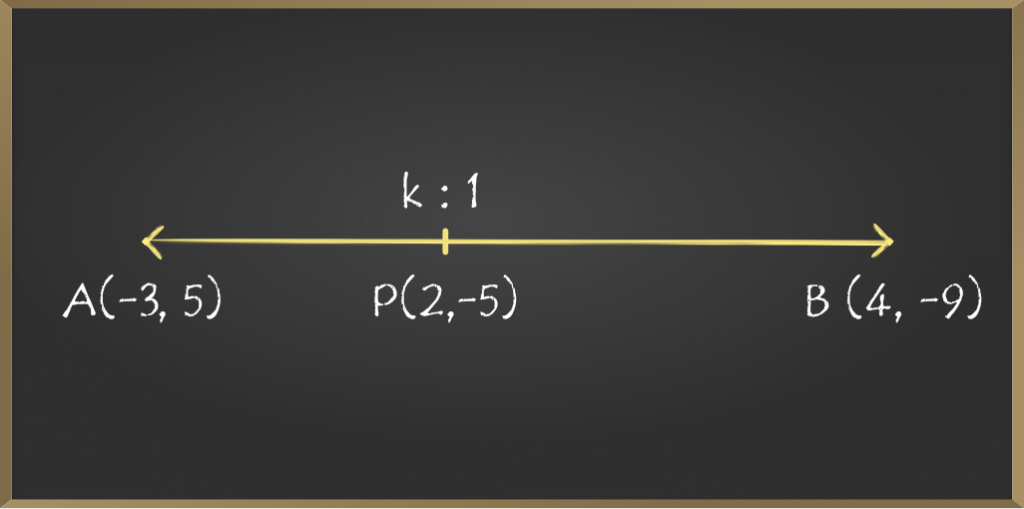
Therefore, Coordinates of P are,
Px = (k.4 + 1.(-3)) / (k + 1)
Py = (k.(-9) + 1 x 5)/(k + 1)
But P is (2, -5) therefore,
(4k – 3) / (k + 1) = 2 and (-9k + 5) / (k + 1) = -5
Solving any of the two equation we get k = 5/2
Therefore, the required ratio is 5/2:1 i.e. 5:2(internally)
Share your thoughts in the comments
Please Login to comment...