In each of the following, give the justification of the construction also:
Question 1. Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Solution:
Steps of construction:
To divide the line segment of 7.6 cm in the ratio of 5 : 8.
Step 1. Draw a line segment AB of length 7.6 cm.
Step 2. Draw a ray AC which forms an acute angle with the line segment AB.
Step 3. Mark the points = 13 as (5+8=13) points, such as A1, A2, A3, A4 …….. A13, on the ray AC such that it becomes AA1 = A1A2 = A2A3 and such like this.
Step 4. Now join the line segment and the ray, BA13.
Step 5. Hence, the point A5, construct a line parallel to BA13 which makes an angle equal to ∠AA13B.
Step 6. Point A5 intersects the line AB at point X.
Step 7. X is that point which divides line segment AB into the ratio of 5:8.
Step 8. Thus, measure the lengths of the line AX and XB. Hence, it measures 2.9 cm and 4.7 cm respectively.

Justification:
The construction can be justified by proving that
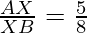
From construction, we have A5X || A13B. By the Basic proportionality theorem for the triangle AA13B, we will get
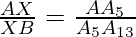 ….. (1)
….. (1)
By the figure we have constructed, it can be seen that AA5 and A5A13 contains 5 and 8 equal divisions of line segments respectively.
Thus,
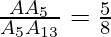 … (2)
… (2)
Comparing the equations (1) and (2), we get
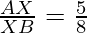
Thus, Justified.
Question 2. Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 2/3 of the corresponding sides of the first triangle.
Solution:
Steps of Construction:
Step 1. Draw a line segment XY which measures 4 cm, So XY = 4 cm.
Step 2. Taking point X as centre, and construct an arc of radius 5 cm.
Step 3. Similarly, from the point Y as centre, and draw an arc of radius 6 cm.
Step 4. Thus, the following arcs drawn will intersect each other at point Z.
Step 5. Now, we have XZ = 5 cm and YZ = 6 cm and therefore ΔXYZ is the required triangle.
Step 6. Draw a ray XA which will make an acute angle along the line segment XY on the opposite side of vertex Z.
Step 7. Mark the 3 points such as X1, X2, X3 (as 3 is greater between 2 and 3) on line XA such that it becomes XX1 = X1X2 = X2X3.
Step 8. Join the point YX3 and construct a line through X2 which is parallel to the line YX3 that intersect XY at point Y’.
Step 9. From the point Y’, construct a line parallel to the line YZ that intersect the line XZ at Z’.
Step 10. Hence, ΔXY’Z’ is the required triangle.

Justification:
The construction can be justified by proving that
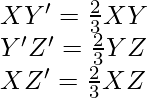
From the construction, we get Y’Z’ || YZ
∴ ∠XY’Z’ = ∠XYZ (Corresponding angles)
In ΔXY’Z’ and ΔXYZ,
∠XYZ = ∠XY’Z (Proved above)
∠YXZ = ∠Y’XZ’ (Common)
∴ ΔXY’Z’ ∼ ΔXYZ (From AA similarity criterion)
Therefore,
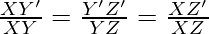 …. (1)
…. (1)
In ΔXXY’ and ΔXXY,
∠X2XY’ =∠X3XY (Common)
From the corresponding angles, we get,
∠AA2B’ =∠AA3B
Thus, by the AA similarity criterion, we get
ΔXX2Y’ and XX3Y
So, 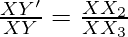
Therefore,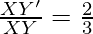 ……. (2)
……. (2)
From the equations (1) and (2), we obtain
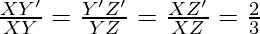
It is written as
XY’ = 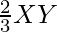
Y’Z’ = 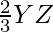
XZ’= 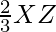
Therefore, justified.
Question 3. Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle
Solution:
Steps of construction:
Step 1. Construct a line segment XY =5 cm.
Step 2. By taking X and Y as centre, and construct the arcs of radius 6 cm and 5 cm respectively.
Step 3. These two arcs will intersect each other at point Z and hence ΔXYZ is the required triangle with the length of sides as 5 cm, 6 cm, and 7 cm respectively.
Step 4. Construct a ray XA which will make an acute angle with the line segment XY on the opposite side of vertex Z.
Step 5. Pinpoint the 7 points such as X1, X2, X3, X4, X5, X6, X7 (as 7 is greater between 5 and 7), on the line XA such that it becomes XX1 = X1X2 = X2X3 = X3X4 = X4X5 = X5X6 = X6X7
Step 6. Join the points YX5 and construct a line from X7 to YX5 that is parallel to the line YX5 where it intersects the extended line segment XY at point Y’.
Step 7. Now, construct a line from Y’ the extended line segment XZ at Z’ that is parallel to the line YZ, and it intersects to make a triangle.
Step 8. Hence, ΔXY’Z’ is the needed triangle.

Justification:
The construction can be justified by proving that
XY’ = 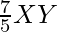
Y’Z’ = 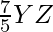
XZ’= 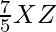
By the construction, we have Y’Z’ || YZ
Therefore,
∠XY’Z’ = ∠XYZ {Corresponding angles}
In ΔXY’Z’ and ΔXYZ,
∠XYZ = ∠XY’Z {As shown above}
∠YXZ = ∠Y’XZ’ {Common}
Therefore,
ΔXY’Z’ ∼ ΔXYZ { By AA similarity criterion}
Therefore,
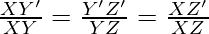 …. (1)
…. (1)
In ΔXX7Y’ and ΔXX5Y,
∠X7XY’=∠X5XY (Common)
From the corresponding angles, we will get,
∠XX7Y’=∠XX5Y
Hence, By the AA similarity criterion, we will get
ΔXX2Y’ and XX3Y
Thus, 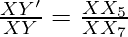
Hence, 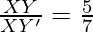 ……. (2)
……. (2)
From the equations (1) and (2), we obtain
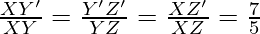
It can be also shown as
XY’ = 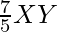
Y’Z’ = 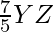
XZ’= 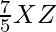
Thus, justified.
Question 4. Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 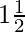 times the corresponding sides of the isosceles triangle
times the corresponding sides of the isosceles triangle
Solution:
Steps of construction:
Step 1. Construct a line segment YZ of 8 cm.
Step 2. Now construct the perpendicular bisector of the line segment YZ and intersect at the point A.
Step 3. Taking the point A as centre and draw an arc with the radius of 4 cm which intersect the perpendicular bisector at the point X.
Step 4. Join the lines XY and XZ and the triangle is the required triangle.
Step 5. Construct a ray YB which makes an acute angle with the line YZ on the side opposite to the vertex X.
Step 6. Mark the 3 points Y1, Y2 and Y3 on the ray YB such that YY1 = Y1Y2 = Y2Y3
Step 7. Join the points Y2Z and construct a line from Y3 which is parallel to the line Y2Z where it intersects the extended line segment YZ at point Z’.
Step 8. Now, draw a line from Z’ the extended line segment XZ at X’, that is parallel to the line XZ, and it intersects to make a triangle.
Step 9. Hence, ΔX’YZ’ is the required triangle.

Justification:
The construction can be justified by proving that
X’Y = 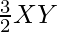
YZ’ = 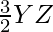
X’Z’= 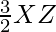
By the construction, we will obtain X’Z’ || XZ
Therefore,
∠ X’Z’Y = ∠XZY {Corresponding angles}
In ΔX’YZ’ and ΔXYZ,
∠Y = ∠Y (common)
∠X’YZ’ = ∠XZY
Therefore,
ΔX’YZ’ ∼ ΔXYZ {By AA similarity criterion}
Hence,
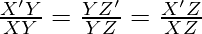
Thus, the corresponding sides of the similar triangle are in the same ratio, we get
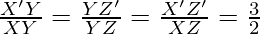
Thus, justified.
Question 5. Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.
Solution:
Steps of construction:
Step 1. Construct a ΔXYZ with base side YZ = 6 cm, and XY = 5 cm and ∠XYZ = 60°.
Step 2. Construct a ray YA that makes an acute angle with YZ on the opposite side of vertex X.
Step 3. Mark 4 points (as 4 is greater in 3 and 4), such as Y1, Y2, Y3, Y4, on line segment YA.
Step 4. Join the points Y4Z and construct a line through Y3, parallel to Y4Z intersecting the line segment YZ at Z’.
Step 5. Construct a line through Z’ parallel to the line XZ which intersects the line XY at X’.
Step 6. Therefore, ΔX’YZ’ is the required triangle.

Justification:
The construction can be justified by proving that
Since here the scale factor is 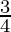 ,
,
We need to prove
X’Y = 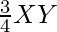
YZ’ = 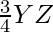
X’Z’= 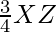
From the construction, we will obtain X’Z’ || XZ
In ΔX’YZ’ and ΔXYZ,
Therefore,
∠X’Z’Y = ∠XZY {Corresponding angles}
∠Y = ∠Y {common}
Therefore,
ΔX’YZ’ ∼ ΔXYZ {By AA similarity criterion}
Thus, the corresponding sides of the similar triangle are in the same ratio, we get
Therefore,
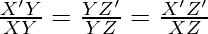
Thus, it becomes
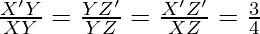
Hence, justified.
Question 6. Draw a triangle ABC with side BC = 7 cm, ∠ B = 45°, ∠ A = 105°. Then, construct a triangle whose sides are 4/3 times the corresponding sides of ∆ ABC.
Solution:
To find ∠Z:
Given:
∠Y = 45°, ∠X = 105°
∠X+∠Y +∠Z = 180° {Sum of all interior angles in a triangle is 180°}
105°+45°+∠Z = 180°
∠Z = 180° − 150°
∠Z = 30°
Thus, from the property of triangle, we get ∠Z = 30°
Steps of construction:
Step 1. Construct a ΔXYZ with side measures of base YZ = 7 cm, ∠Y = 45°, and ∠Z = 30°.
Step 2. Construct a ray YA makes an acute angle with YZ on the opposite side of vertex X.
Step 3. Mark 4 points (as 4 is greater in 4 and 3), such as Y1, Y2, Y3, Y4, on the ray YA.
Step 4. Join the points Y3Z.
Step 5. Construct a line through Y4 parallel to Y3Z which intersects the extended line YZ at Z’.
Step 6. Through Z’, construct a line parallel to the line YZ that intersects the extended line segment at Z’.
Step 7. Hence, ΔX’YZ’ is the required triangle.

Justification:
The construction can be justified by proving that
Here the scale factor is 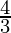 , we have to prove
, we have to prove
X’Y = 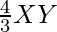
YZ’ = 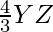
X’Z’= 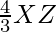
From the construction, we obtain X’Z’ || XZ
In ΔX’YZ’ and ΔXYZ,
Therefore.
∠X’Z’Y = ∠XZY {Corresponding angles}
∠Y = ∠Y {common}
Therefore,
ΔX’YZ’ ∼ ΔXYZ {By AA similarity criterion}
Since the corresponding sides of the similar triangle are in the same ratio, it becomes
Therefore,
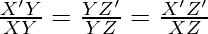
We get,
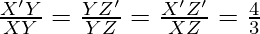
Thus, justified.
Question 7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Solution:
Given:
The sides other than hypotenuse are of lengths 4cm and 3cm. Hence, the sides are perpendicular to each other.
Step of construction:
Step 1. Construct a line segment YZ =3 cm.
Step 2. Now measure and draw ∠= 90°
Step 3. Now taking Y as centre and draw an arc with the radius of 4 cm and intersects the ray at the point Y.
Step 4. Join the lines XZ and the triangle XYZ is the required triangle.
Step 5. Construct a ray YA makes an acute angle with YZ on the opposite side of vertex X.
Step 6. Mark 5 such as Y1, Y2, Y3, Y4, on the ray YA such that YY1 = Y1Y2 = Y2Y3= Y3Y4 = Y4Y5
Step 7. Join the points Y3Z.
Step 8. Construct a line through Y5 parallel to Y3Z which intersects the extended line YZ at Z’.
Step 9. Through Z’, draw a line parallel to the line XZ that intersects the extended line XY at X’.
Step 10. Therefore, ΔX’YZ’ is the required triangle.

Justification:
The construction can be justified by proving that
Here the scale factor is 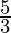 , we need to prove
, we need to prove
X’Y = 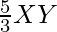
YZ’ = 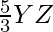
X’Z’= 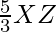
From the construction, we obtain X’Z’ || XZ
In ΔX’YZ’ and ΔXYZ,
Therefore,
∠X’Z’Y = ∠XZY {Corresponding angles}
∠Y = ∠Y {common}
Therefore,
ΔX’YZ’ ∼ ΔXYZ {By AA similarity criterion}
Since the corresponding sides of the similar triangle are in the same ratio, it becomes
Therefore,
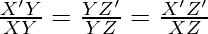
So, it becomes 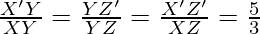
Therefore, justified.
Share your thoughts in the comments
Please Login to comment...