Draw circle using polar equation and Bresenham’s equation
Last Updated :
23 Mar, 2024
In this article, we will discuss how to draw circles using Bresenham Equation and Polar Equation.
Circle Drawing Algorithm
It is not easy to display a continuous smooth arc on the computer screen as our computer screen is made of pixels organized in matrix form. So, to draw a circle on a computer screen it should always choose the nearest pixels from a printed pixel so as they could form an arc.
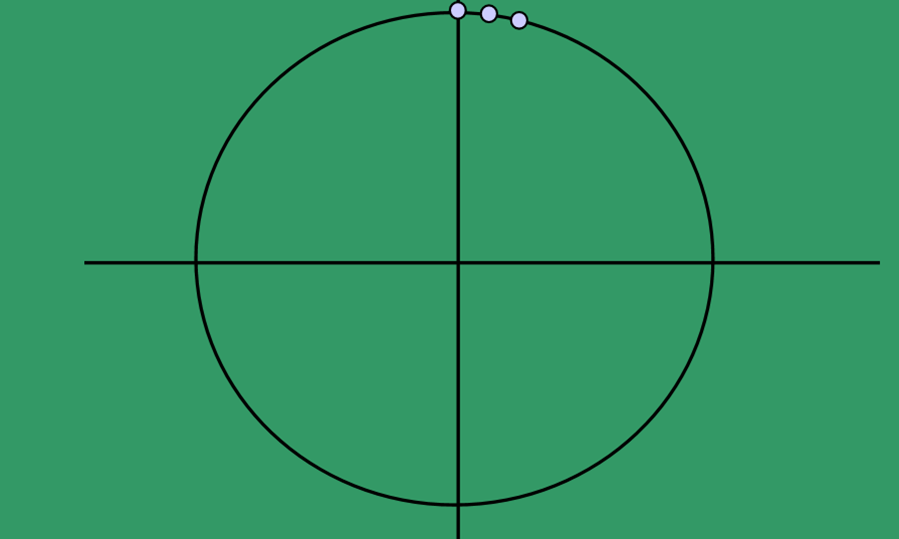
- Consider circles centered at the origin with integer radii.
- Can apply translations to get non-origin centered circles.
Equation of circle is given by:
x2 + y2 = R2
y = +/-sqrt(R2-x2)
- The given equation can be written as:
F(x, y)= x2+ y2-R2=0
5.
- Use of Symmetry: Only need to calculate one octant. One can get points in the other 7 octants as follows:
- Plotpoint(x, y)
- Plotpoint(y, x)
- Plotpoint(x, -y)
- Plotpoint(-y, x)
- Plotpoint(-x, -y)
- Plotpoint(-y, -x)
- Plotpoint(-x, y)
- Plotpoint(-y, x)
Circle Drawing Using Bresenham Equation
Bresenham Equation uses the key feature of a circle that is highly symmetric. So, for the whole 360 degrees circle, divide it into 8-parts each octant of 45 degrees. In order to that, the idea is to use Bresenham’s Circle Algorithm for the calculation of the locations of the pixels in the first octant of 45 degrees. It assumes that the circle is centered on the origin. So for every pixel (x, y) draw a pixel in each of the 8 octants of the circle as shown below:

In Bresenham’s Algorithm at any point (x, y) we have two options either to choose the next pixel in the east i.e., (x + 1, y) or in the south-east i.e., (x + 1, y – 1). And this can be decided by using the decision parameter d as:
- If d > 0, then (x + 1, y – 1) is to be chosen as the next pixel as it will be closer to the arc.
- Else (x + 1, y) is to be chosen as the next pixel.
Below is the algorithm for Bresenham Equation:
- F(x, y) = x2 + y2 = 0 Point lies on the circle.
- F(x, y) > 0 Point lies outside the circle.
- F(x, y) < 0 Point lies inside the circle.
- If d >= 0 then update x as (x + 1) and y = (y – 1) which gives new d
- If d < 0 then update x as (x + 1) which gives the new value of d
C++
#include <GL/glut.h>
#include <iostream>
float xo = 0, yo = 0, r = 0;
void drawCircle() {
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1, 0, 0);
glPointSize(2);
float x = 0;
float y = r;
float p = 5 / 4.0f - r;
glBegin(GL_POINTS);
while (y > x) {
if (p < 0) {
x += 1;
p = p + 2 * x + 1;
} else {
y -= 1;
x += 1;
p = p + 2 * (x - y) + 1;
}
glVertex2f(x + xo, y + yo);
glVertex2f(-x + xo, y + yo);
glVertex2f(x + xo, -y + yo);
glVertex2f(-x + xo, -y + yo);
glVertex2f(y + yo, x + xo);
glVertex2f(-y + yo, x + xo);
glVertex2f(y + yo, -x + xo);
glVertex2f(-y + yo, -x + xo);
}
glEnd();
glFlush();
}
void init() {
glClearColor(1, 1, 1, 1);
glOrtho(-500, 500, -500, 500, -1, 1);
}
int main(int argc, char** argv) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(1000, 1000);
glutInitWindowPosition(100, 100);
glutCreateWindow("GeeksforGeeks");
std::cout << "Enter X, Y, and radius in the console." << std::endl;
std::cout << "Enter X-coordinate: ";
std::cin >> xo;
std::cout << "Enter Y-coordinate: ";
std::cin >> yo;
std::cout << "Enter radius: ";
std::cin >> r;
init();
glutDisplayFunc(drawCircle);
glutMainLoop();
return 0;
}
//This code is contributed by Utkarsh
// C program for the above approach
#include <GL/gl.h>
#include <GL/glut.h>
#include <math.h>
#include <stdio.h>
int xo, yo, r;
// Function to display the circle using
// the above algorithm
void Display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
// Color of printing object
glColor3f(1, 0, 0);
// Giving the size of the point
glPointSize(2);
int x = 0;
int y = r;
float p = 5 / 4 - r;
glColor3f(1, 0, 0);
// Starting of drawing the circle
glBegin(GL_POINTS);
while (y > x) {
if (p < 0) {
// Increment x to x+1
x++;
p = p + 2 * x + 1;
}
else {
// Increment x to x+1
// and decrease y to y-1
y--;
x++;
p = p + 2 * (x - y) + 1;
}
// Draw the coordinates
glVertex2d(x + xo, y + yo);
glVertex2d(-x + xo, y + yo);
glVertex2d(x + xo, -y + yo);
glVertex2d(-x + xo, -y + yo);
glVertex2d(y + yo, x + xo);
glVertex2d(-y + yo, x + xo);
glVertex2d(y + yo, -x + xo);
glVertex2d(-y + yo, -x + xo);
}
glEnd();
// Its empties all the buffer
// causing the issue
glFlush();
}
// Driver Code
int main(int argc, char** argv)
{
printf("X-coordinate Y-coordinate radius:");
scanf("%d %d %d", &xo, &yo, &r);
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
// Assigning the size of window
glutInitWindowSize(1000, 1000);
// Assign the position of window
// to be appeared
glutInitWindowPosition(100, 100);
// Defining the heading of the window
glutCreateWindow("GeeksforGeeks");
// Backgronnd Color
glClearColor(1, 1, 1, 1);
// limit of the coordinate points
gluOrtho2D(-500, 500, -500, 500);
// Calling the function
glutDisplayFunc(Display);
glutMainLoop();
return 0;
}
import javax.swing.*;
import javax.media.opengl.*;
import java.awt.*;
public class CircleDrawing extends JFrame implements GLEventListener {
private static final long serialVersionUID = 1L;
private float xo = 0, yo = 0, r = 0;
public static void main(String[] args) {
SwingUtilities.invokeLater(() -> {
new CircleDrawing().setVisible(true);
});
}
public CircleDrawing() {
setTitle("GeeksforGeeks");
setSize(1000, 1000);
setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
GLCanvas canvas = new GLCanvas();
canvas.addGLEventListener(this);
add(canvas);
setVisible(true);
JOptionPane.showMessageDialog(this, "Enter X, Y, and radius in the console.");
xo = Float.parseFloat(JOptionPane.showInputDialog("Enter X-coordinate:"));
yo = Float.parseFloat(JOptionPane.showInputDialog("Enter Y-coordinate:"));
r = Float.parseFloat(JOptionPane.showInputDialog("Enter radius:"));
}
@Override
public void init(GLAutoDrawable drawable) {
GL gl = drawable.getGL();
gl.glClearColor(1, 1, 1, 1);
gl.glOrtho(-500, 500, -500, 500, -1, 1);
}
@Override
public void display(GLAutoDrawable drawable) {
GL gl = drawable.getGL();
GLU glu = new GLU();
gl.glClear(GL.GL_COLOR_BUFFER_BIT);
// Color of printing object
gl.glColor3f(1, 0, 0);
// Giving the size of the point
gl.glPointSize(2);
float x = 0;
float y = r;
float p = 5 / 4.0f - r;
// Starting of drawing the circle
gl.glBegin(GL.GL_POINTS);
while (y > x) {
if (p < 0) {
// Increment x to x+1
x += 1;
p = p + 2 * x + 1;
} else {
// Increment x to x+1 and decrease y to y-1
y -= 1;
x += 1;
p = p + 2 * (x - y) + 1;
}
// Draw the coordinates
gl.glVertex2d(x + xo, y + yo);
gl.glVertex2d(-x + xo, y + yo);
gl.glVertex2d(x + xo, -y + yo);
gl.glVertex2d(-x + xo, -y + yo);
gl.glVertex2d(y + yo, x + xo);
gl.glVertex2d(-y + yo, x + xo);
gl.glVertex2d(y + yo, -x + xo);
gl.glVertex2d(-y + yo, -x + xo);
}
gl.glEnd();
// Flush all the buffer causing the issue
gl.glFlush();
}
@Override
public void reshape(GLAutoDrawable drawable, int x, int y, int width, int height) {
}
@Override
public void dispose(GLAutoDrawable drawable) {
}
// This Code is Contributed by Shivam Tiwari
}
from OpenGL.GL import *
from OpenGL.GLUT import *
import math
xo, yo, r = 0, 0, 0
# Function to display the circle using the above algorithm
def Display():
glClear(GL_COLOR_BUFFER_BIT)
# Color of printing object
glColor3f(1, 0, 0)
# Giving the size of the point
glPointSize(2)
x = 0
y = r
p = 5 / 4.0 - r # Corrected the division to use floating-point arithmetic
glColor3f(1, 0, 0)
# Starting of drawing the circle
glBegin(GL_POINTS)
while y > x:
if p < 0:
# Increment x to x+1
x += 1
p = p + 2 * x + 1
else:
# Increment x to x+1 and decrease y to y-1
y -= 1
x += 1
p = p + 2 * (x - y) + 1
# Draw the coordinates
glVertex2d(x + xo, y + yo)
glVertex2d(-x + xo, y + yo)
glVertex2d(x + xo, -y + yo)
glVertex2d(-x + xo, -y + yo)
glVertex2d(y + yo, x + xo)
glVertex2d(-y + yo, x + xo)
glVertex2d(y + yo, -x + xo)
glVertex2d(-y + yo, -x + xo)
glEnd()
# Flush all the buffer causing the issue
glFlush()
# Driver Code
def main():
global xo, yo, r
xo, yo, r = map(int, input("X-coordinate Y-coordinate radius:").split())
glutInit()
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB)
# Assigning the size of window
glutInitWindowSize(1000, 1000)
# Assign the position of window to be appeared
glutInitWindowPosition(100, 100)
# Defining the heading of the window
glutCreateWindow(b"GeeksforGeeks")
# Background Color
glClearColor(1, 1, 1, 1)
# Limit of the coordinate points
gluOrtho2D(-500, 500, -500, 500)
# Calling the function
glutDisplayFunc(Display)
glutMainLoop()
if __name__ == "__main__":
main()
using System;
using OpenTK;
using OpenTK.Graphics;
using OpenTK.Graphics.OpenGL;
using OpenTK.Input;
namespace CircleDrawing
{
class Program : GameWindow
{
// Center coordinates (X, Y) and radius (r) for the circle
float xo = 0, yo = 0, r = 0;
// Constructor to initialize the OpenTK window
public Program(int width, int height) : base(width, height, GraphicsMode.Default, "GeeksforGeeks")
{
// Prompt user to input circle parameters
Console.WriteLine("Enter X, Y, and radius in the console.");
Console.Write("Enter X-coordinate: ");
xo = float.Parse(Console.ReadLine());
Console.Write("Enter Y-coordinate: ");
yo = float.Parse(Console.ReadLine());
Console.Write("Enter radius: ");
r = float.Parse(Console.ReadLine());
// Set vertical synchronization for smoother rendering
VSync = VSyncMode.On;
}
// Method to draw the circle using the midpoint circle drawing algorithm
void DrawCircle()
{
// Clear the color buffer
GL.Clear(ClearBufferMask.ColorBufferBit);
// Set the drawing color to red
GL.Color3(1.0f, 0.0f, 0.0f);
// Set the point size to 2 pixels
GL.PointSize(2.0f);
// Initialize circle drawing variables
float x = 0;
float y = r;
float p = 5 / 4.0f - r;
// Begin drawing points
GL.Begin(PrimitiveType.Points);
// Loop to draw the circle points
while (y > x)
{
if (p < 0)
{
x += 1;
p = p + 2 * x + 1;
}
else
{
y -= 1;
x += 1;
p = p + 2 * (x - y) + 1;
}
// Draw points in all octants
GL.Vertex2(x + xo, y + yo);
GL.Vertex2(-x + xo, y + yo);
GL.Vertex2(x + xo, -y + yo);
GL.Vertex2(-x + xo, -y + yo);
GL.Vertex2(y + yo, x + xo);
GL.Vertex2(-y + yo, x + xo);
GL.Vertex2(y + yo, -x + xo);
GL.Vertex2(-y + yo, -x + xo);
}
// End drawing points
GL.End();
// Swap the front and back buffers for double buffering
SwapBuffers();
}
// Method to initialize OpenGL settings
protected override void OnLoad(EventArgs e)
{
// Set the clear color to white
GL.ClearColor(1.0f, 1.0f, 1.0f, 1.0f);
// Set the orthographic projection matrix
GL.Ortho(-500, 500, -500, 500, -1, 1);
}
// Method called on each frame to render the circle
protected override void OnRenderFrame(FrameEventArgs e)
{
DrawCircle();
}
// Main method to create and run the program
[STAThread]
static void Main()
{
// Create an instance of the Program class with a window size of 1000x1000
using (Program program = new Program(1000, 1000))
{
// Run the program with a target frame rate of 30 frames per second
program.Run(30);
}
}
}
}
let xo = 0, yo = 0, r = 0;
// Function to display the circle using the above algorithm
function Display() {
glClear(GL_COLOR_BUFFER_BIT);
// Color of printing object
glColor3f(1, 0, 0);
// Giving the size of the point
glPointSize(2);
let x = 0;
let y = r;
let p = 5 / 4.0 - r; // Corrected the division to use floating-point arithmetic
glColor3f(1, 0, 0);
// Starting of drawing the circle
glBegin(GL_POINTS);
while (y > x) {
if (p < 0) {
// Increment x to x+1
x += 1;
p = p + 2 * x + 1;
} else {
// Increment x to x+1 and decrease y to y-1
y -= 1;
x += 1;
p = p + 2 * (x - y) + 1;
}
// Draw the coordinates
glVertex2d(x + xo, y + yo);
glVertex2d(-x + xo, y + yo);
glVertex2d(x + xo, -y + yo);
glVertex2d(-x + xo, -y + yo);
glVertex2d(y + yo, x + xo);
glVertex2d(-y + yo, x + xo);
glVertex2d(y + yo, -x + xo);
glVertex2d(-y + yo, -x + xo);
}
glEnd();
// Flush all the buffer causing the issue
glFlush();
}
// Driver Code
function main() {
xo = prompt("Enter X-coordinate:");
yo = prompt("Enter Y-coordinate:");
r = prompt("Enter radius:");
glutInit();
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
// Assigning the size of window
glutInitWindowSize(1000, 1000);
// Assign the position of window to be appeared
glutInitWindowPosition(100, 100);
// Defining the heading of the window
glutCreateWindow("GeeksforGeeks");
// Background Color
glClearColor(1, 1, 1, 1);
// Limit of the coordinate points
gluOrtho2D(-500, 500, -500, 500);
// Calling the function
glutDisplayFunc(Display);
glutMainLoop();
}
// This Code is Contributed by Shivam Tiwari
Output:

Time Complexity: O(N)
Auxiliary Space: O(1)
Circle Using Polar Equation
In the Polar Equation system, the idea is to think of a clock with one hand. Move out a distance r, sometimes called the modulus, along with the hand from the origin, then rotate the hand upward (counterclockwise) by an angle θ to reach the point. Below is the algorithm for the Polar Equation:
- Initialize the variables rad, center(x0, y0), index value or increment value i, and define a circle using polar coordinates θ_end = 100.
- If θ_end < θ, then exit from the loop.
- Find the value of x as rad*cos(angle) and y as rad*sin(angle).
- Plot the eight points, found by symmetry i.e., the center (x0, y0) at the current (x, y) coordinates.
- Plot (x + xo, y + yo)
- Plot (-x + xo, -y + yo)
- Plot (y + xo, x + yo)
- Plot (-y + xo, -x + yo)
- Plot (-y + xo, x + yo)
- Plot (y + xo, -x + yo)
- Plot (-x + xo, y + yo)
- Plot (x + xo, -y + yo)
- Increment the angle by i*2*(M_PI/100).
Below is the program to implement the above approach:
C++
#include <iostream>
#include <SDL.h>
#include <OpenGL/gl.h>
#include <OpenGL/glu.h>
#include <cmath>
void display(float xo, float yo, float rad) {
// Clear previous frame
glClear(GL_COLOR_BUFFER_BIT);
// Set drawing color to white
glColor3f(1, 1, 1);
float angle = 0;
// Begin drawing a polygon
glBegin(GL_POLYGON);
// Loop through 100 points to form the circle
for (int i = 0; i < 100; ++i) {
angle = i * 2 * (M_PI / 100);
// Calculate x and y coordinates based on the angle and radius
glVertex2f(xo + (cos(angle) * rad),
yo + (sin(angle) * rad));
}
glEnd();
// Update the display
SDL_GL_SwapBuffers();
}
int main(int argc, char* argv[]) {
// Initialize SDL
if (SDL_Init(SDL_INIT_VIDEO) < 0) {
std::cerr << "Failed to initialize SDL: " << SDL_GetError() << std::endl;
return 1;
}
// Take input values for x, y coordinates, and radius
float xo, yo, rad;
std::cout << "Enter x y radius: ";
std::cin >> xo >> yo >> rad;
// Set OpenGL attributes
SDL_GL_SetAttribute(SDL_GL_DOUBLEBUFFER, 1);
SDL_GL_SetAttribute(SDL_GL_DEPTH_SIZE, 24);
SDL_GL_SetAttribute(SDL_GL_RED_SIZE, 8);
SDL_GL_SetAttribute(SDL_GL_GREEN_SIZE, 8);
SDL_GL_SetAttribute(SDL_GL_BLUE_SIZE, 8);
SDL_GL_SetAttribute(SDL_GL_ALPHA_SIZE, 8);
// Create window
SDL_Surface* screen = SDL_SetVideoMode(500, 500, 32, SDL_OPENGL);
if (!screen) {
std::cerr << "Failed to set video mode: " << SDL_GetError() << std::endl;
SDL_Quit();
return 1;
}
// Set the window title
SDL_WM_SetCaption("GeeksforGeeks", nullptr);
// Set background color to green
glClearColor(0, 1, 0, 1);
// Setting the coordinate limits for drawing
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(-500, 500, -500, 500);
glMatrixMode(GL_MODELVIEW);
bool running = true;
SDL_Event event;
// Event loop to keep the window running and listen for events
while (running) {
while (SDL_PollEvent(&event)) {
if (event.type == SDL_QUIT) {
running = false;
}
}
// Draw the circle in each frame
display(xo, yo, rad);
}
// Close the SDL window
SDL_Quit();
return 0;
}
//Thi code is contributed by Prachi.
// C program to demonstrate circle
// drawing using polar equation
#include <GL/glut.h>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
float xo, yo, rad;
// Function to display the circle
void display()
{
glClear(GL_COLOR_BUFFER_BIT);
// Color of printing object
glColor3f(1, 1, 1);
float angle;
// Start to drawing the circle
glBegin(GL_POLYGON);
for (int i = 0; i < 100; i++) {
// Change the angle
angle = i * 2 * (M_PI / 100);
glVertex2f(xo + (cos(angle) * rad),
yo + (sin(angle) * rad));
}
glEnd();
// Its empties all the buffer
// causing the issue
glFlush();
}
// Driver Code
int main(int argc, char** argv)
{
glutInit(&argc, argv);
printf("Enter x y radius ");
scanf("%f %f %f", &xo, &yo, &rad);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
// Assigning the size of window
glutInitWindowSize(500, 500);
// Assign the position of window
// to be appeared
glutInitWindowPosition(200, 200);
// Defining the heading of the window
glutCreateWindow("GeeksforGeeks");
// Backgronnd Color
glClearColor(0, 1, 0, 1);
// limit of the coordinate points
gluOrtho2D(-500, 500, -500, 500);
// Calling the function
glutDisplayFunc(Display);
glutMainLoop();
return 0;
}
import org.lwjgl.LWJGLException;
import org.lwjgl.opengl.Display;
import org.lwjgl.opengl.DisplayMode;
import org.lwjgl.opengl.GL11;
import org.lwjgl.util.glu.GLU;
import java.util.Scanner;
public class Main {
// Function to display the circle
public static void display(float xo, float yo, float rad) {
// Clear the screen
GL11.glClear(GL11.GL_COLOR_BUFFER_BIT);
// Set drawing color to white
GL11.glColor3f(1, 1, 1);
float angle = 0;
// Begin drawing a polygon
GL11.glBegin(GL11.GL_POLYGON);
// Loop through 100 points to form the circle
for (int i = 0; i < 100; ++i) {
angle = i * 2 * (float) Math.PI / 100;
// Calculate x and y coordinates based on the angle and radius
GL11.glVertex2f(xo + (float) Math.cos(angle) * rad,
yo + (float) Math.sin(angle) * rad);
}
GL11.glEnd();
// Update the display
Display.update();
}
public static void main(String[] args) {
try {
// Create the display
Display.setDisplayMode(new DisplayMode(500, 500));
Display.setTitle("GeeksforGeeks");
Display.create();
} catch (LWJGLException e) {
e.printStackTrace();
System.exit(1);
}
// Set background color to green
GL11.glClearColor(0, 1, 0, 1);
// Setting the coordinate limits for drawing
GL11.glMatrixMode(GL11.GL_PROJECTION);
GL11.glLoadIdentity();
GLU.gluOrtho2D(-500, 500, -500, 500);
GL11.glMatrixMode(GL11.GL_MODELVIEW);
// Take input values for x, y coordinates, and radius
Scanner scanner = new Scanner(System.in);
System.out.print("Enter x y radius: ");
float xo = scanner.nextFloat();
float yo = scanner.nextFloat();
float rad = scanner.nextFloat();
// Event loop to keep the window running and listen for events
while (!Display.isCloseRequested()) {
// Draw the circle in each frame
display(xo, yo, rad);
}
// Close the display
Display.destroy();
}
}
//This code is contributed by Monu.
using System;
using OpenTK;
using OpenTK.Graphics;
using OpenTK.Graphics.OpenGL;
class Program
{
static void Display(float xo, float yo, float rad)
{
// Clear previous frame
GL.Clear(ClearBufferMask.ColorBufferBit);
// Set drawing color to white
GL.Color3(1.0f, 1.0f, 1.0f);
float angle = 0;
// Begin drawing a polygon
GL.Begin(PrimitiveType.Polygon);
// Loop through 100 points to form the circle
for (int i = 0; i < 100; ++i)
{
angle = i * 2 * (float)Math.PI / 100;
// Calculate x and y coordinates based on the angle and radius
GL.Vertex2(xo + (float)Math.Cos(angle) * rad,
yo + (float)Math.Sin(angle) * rad);
}
GL.End();
// Update the display
GL.Flush();
}
static void Main(string[] args)
{
using (var window = new GameWindow())
{
// Take input values for x, y coordinates, and radius
float xo, yo, rad;
Console.Write("Enter x y radius: ");
string[] input = Console.ReadLine().Split();
if (input.Length != 3 || !float.TryParse(input[0], out xo) || !float.TryParse(input[1], out yo) || !float.TryParse(input[2], out rad))
{
Console.WriteLine("Invalid input. Please enter three float values separated by spaces.");
return;
}
// Set OpenGL version and attributes
var glVersion = new GraphicsMode(new ColorFormat(32), 24, 8, 4);
var glControl = new GraphicsContext(glVersion, window.WindowInfo);
// Make the OpenGL context current
glControl.MakeCurrent(window.WindowInfo);
// Set background color to green
GL.ClearColor(0.0f, 1.0f, 0.0f, 1.0f);
window.Load += (sender, e) =>
{
// Drawing settings
GL.MatrixMode(MatrixMode.Projection);
GL.LoadIdentity();
GL.Ortho(-500, 500, -500, 500, -1, 1);
GL.MatrixMode(MatrixMode.Modelview);
};
window.Resize += (sender, e) =>
{
// Update viewport on window resize
GL.Viewport(0, 0, window.Width, window.Height);
};
window.RenderFrame += (sender, e) =>
{
// Draw the circle in each frame
Display(xo, yo, rad);
window.SwapBuffers();
};
// Run the application loop
window.Run();
}
}
}
//This code is contribiuuted by Utkarsh.
let xo, yo, rad;
function display() {
gl.clear(gl.COLOR_BUFFER_BIT);
// Color of printing object
gl.color3f(1, 1, 1);
let angle;
// Start drawing the circle
gl.begin(gl.POLYGON);
for (let i = 0; i < 100; i++) {
// Change the angle
angle = i * 2 * (Math.PI / 100);
gl.vertex2f(xo + Math.cos(angle) * rad, yo + Math.sin(angle) * rad);
}
gl.end();
// Flush the buffer
gl.flush();
}
function main() {
const canvas = document.createElement("canvas");
document.body.appendChild(canvas);
const gl = canvas.getContext("webgl");
if (!gl) {
console.log("Unable to initialize WebGL. Your browser may not support it.");
return;
}
console.log("Enter x y radius (separated by spaces):");
// You might want to replace this with a form of user input
// For simplicity, you can hardcode values here.
xo = 0;
yo = 0;
rad = 50;
gl.clearColor(0, 1, 0, 1);
gl.ortho(-500, 500, -500, 500, -1, 1);
// Calling the function
gl.displayFunc(display);
// Event listener for closing the window
window.addEventListener('beforeunload', () => {
// Clean up resources if needed
// gl.deleteProgram(program);
});
gl.mainLoop();
// This Code is Contributed by Shivam Tiwari
}
import pygame
from pygame.locals import *
from OpenGL.GL import *
from OpenGL.GLUT import *
import math
def display():
# Clear previous frame
glClear(GL_COLOR_BUFFER_BIT)
# Set drawing color to white
glColor3f(1, 1, 1)
angle = 0
# Begin drawing a polygon
glBegin(GL_POLYGON)
# Loop through 100 points to form the circle
for i in range(100):
angle = i * 2 * (math.pi / 100)
# Calculate x and y coordinates based on the angle and radius
glVertex2f(xo + (math.cos(angle) * rad),
yo + (math.sin(angle) * rad))
glEnd()
# Update the display
pygame.display.flip()
if __name__ == "__main__":
# Initialize pygame
pygame.init()
# Take input values for x, y coordinates and radius
xo, yo, rad = map(float, input("Enter x y radius: ").split())
display_mode = pygame.OPENGL | pygame.DOUBLEBUF
# Set up display mode and window size
pygame.display.set_mode((500, 500), display_mode)
# Set the window title
pygame.display.set_caption("GeeksforGeeks")
# Set background color to green
glClearColor(0, 1, 0, 1)
# Setting the coordinate limits for drawing
gluOrtho2D(-500, 500, -500, 500)
running = True
# Event loop to keep the window running and listen for events
while running:
for event in pygame.event.get():
# Check for window close event
if event.type == pygame.QUIT:
running = False
# Draw the circle in each frame
display()
# Close the pygame window
pygame.quit()
# This Code Is Contributed By Shubham Tiwari
Output:

Time Complexity: O(N)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...