Program to find all possible triangles having same Area and Perimeter

The task is to find all possible triangles having the same perimeter and area.

Examples:

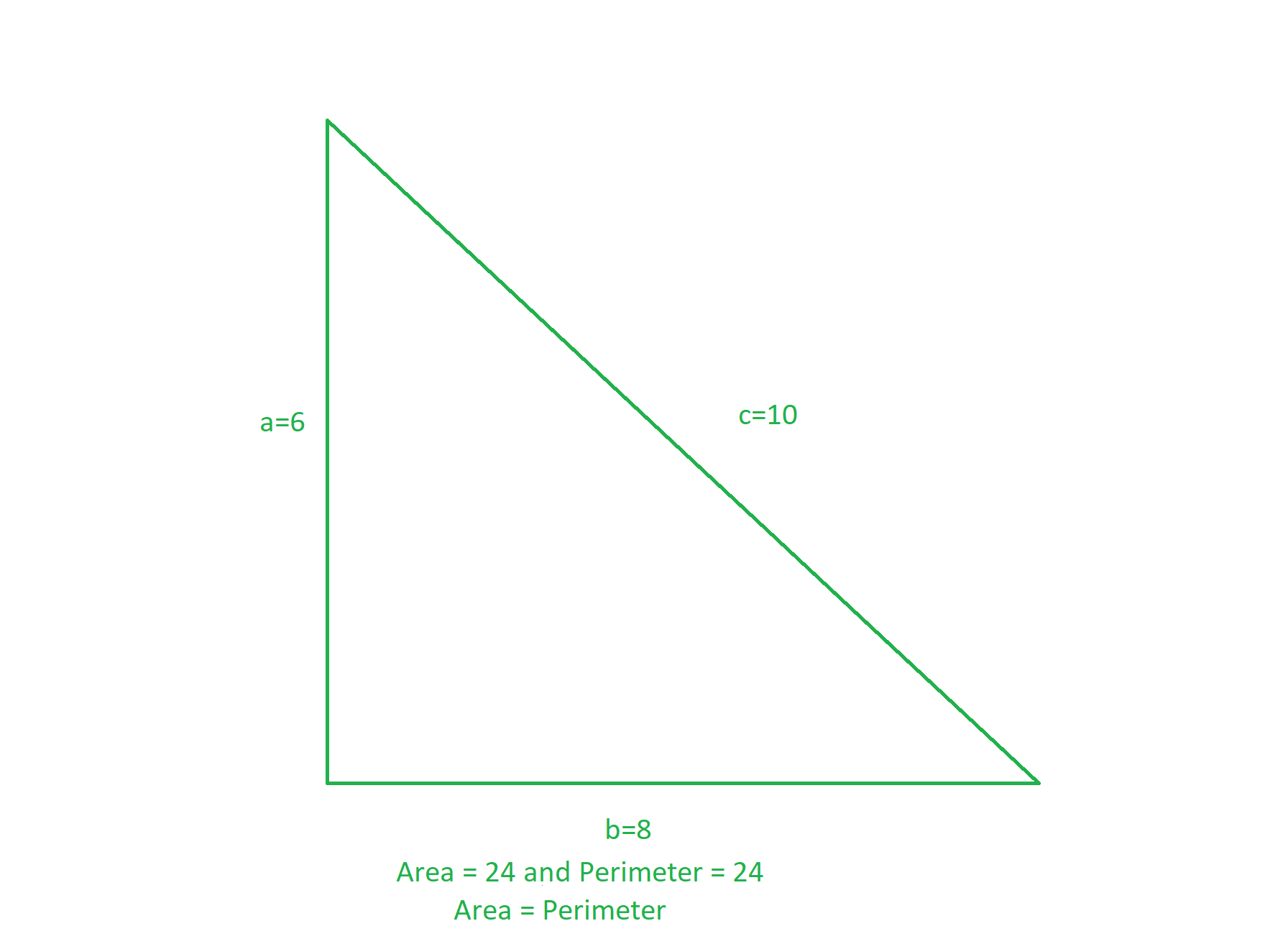
The triangle having sides (6, 8, 10) have the same perimeter (= (6 + 8 + 10) = 24) and area (= 0.5 * 6 * 8 = 24).

Approach: The idea is based on the observation from Heron’s Formula. Below are the observations: 

Let the sides of the triangle be a, b, c.
Perimeter(P) = a + b + c
Area(A) using Heron’s Formula:

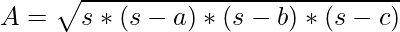
where s = (a + b + c) / 2  

Experimental Observation:

We know that:
4 * s² = s * (s – a) * (s – b) * (s – c)
=> 4 * s = (s – a) * (s – b) * (s – c)
=> 2 * 2 * 2 * 4 * s = 2 * (s – a) * 2 * (s -b) * 2 * (s – c)
=> 16 * (a + b + c) = (- a + b + c) * (a – b + c) * (a + b – c)

Due to this condition:
Max value of (- a + b + c), (a – b + c), (a + b – c) is as follows:
(- a + b + c) * (a – b + c) * (a + b – c) ≤ 16 * 16 * 16
=> 16 * (a + b + c) ≤ 16 * 16 * 16
=> (a + b + c) ≤ 256

From the above equation, the sum of sides of the triangle doesn’t exceed 256 whose perimeter of triangle and area of the triangle can be the same. Therefore, the idea is to iterate three nested loops over the range [1, 256] and print those triplets of sides having the same area and perimeter.

Below is the implementation of the above approach: 

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

// Function to print sides of all the
// triangles having same perimeter & area
void samePerimeterAndArea()
{
    // Stores unique sides of triangles
    set<vector<int> > se;

    // i + j + k values cannot exceed 256
    for (int i = 1; i <= 256; ++i) {

        for (int j = 1; j <= 256; ++j) {

            for (int k = 1; k <= 256; ++k) {

                // Find the value of 2 * s
                int peri = i + j + k;

                // Find the value of
                // 2 * ( s - a )
                int mul1 = -i + j + k;

                // Find the value of
                // 2 * ( s - b )
                int mul2 = i - j + k;

                // Find the value of
                // 2 * ( s - c )
                int mul3 = i + j - k;

                // If triplets have same
                // area and perimeter
                if (16 * peri == mul1 * mul2 * mul3) {

                    // Store sides of triangle
                    vector<int> v = { i, j, k };

                    // Sort the triplets
                    sort(v.begin(), v.end());

                    // Inserting in set to
                    // avoid duplicate sides
                    se.insert(v);
                }
            }
        }
    }

    // Print sides of all desired triangles
    for (auto it : se) {
        cout << it[0] << " "
             << it[1] << " "
             << it[2] << endl;
    }
}

// Driver Code
int main()
{
    // Function call
    samePerimeterAndArea();

    return 0;
}

Java

/*package whatever //do not write package name here */
// Java program for the above approach
import java.io.*;
import java.util.*;

public class GFG {

  // Function to print sides of all the
  // triangles having same perimeter & area
  static void samePerimeterAndArea()
  {

    // Stores unique sides of triangles
    Set<ArrayList<Integer>> se = new HashSet<ArrayList<Integer>>();

    // i + j + k values cannot exceed 256
    for (int i = 1; i <= 256; ++i) {

      for (int j = 1; j <= 256; ++j) {

        for (int k = 1; k <= 256; ++k) {

          // Find the value of 2 * s
          int peri = i + j + k;

          // Find the value of
          // 2 * ( s - a )
          int mul1 = -i + j + k;

          // Find the value of
          // 2 * ( s - b )
          int mul2 = i - j + k;

          // Find the value of
          // 2 * ( s - c )
          int mul3 = i + j - k;

          // If triplets have same
          // area and perimeter
          if (16 * peri == mul1 * mul2 * mul3) {

            // Store sides of triangle
            ArrayList<Integer> v=new ArrayList<Integer>();
            v.add(i);
            v.add(j);
            v.add(k);

            // Sort the triplets
            Collections.sort(v);

            // Inserting in set to
            // avoid duplicate sides
            se.add(v);
          }
        }
      }
    }

    // Print sides of all desired triangles
    for (ArrayList<Integer> it : se) {
      System.out.println(it.get(0) + " " + it.get(1) + " " + it.get(2));
    }
  }

  // Driver Code
  public static void main(String[] args)
  {

    // Function Call
    samePerimeterAndArea();
  }
}

// The code is contributed by Gautam goel (gautamgoel962)

Python3

# Python3 program for the above approach

# Function to print sides of all the
# triangles having same perimeter & area
def samePerimeterAndArea():

    # Stores unique sides of triangles
    se = []

    # i + j + k values cannot exceed 256
    for i in range(1, 256, 1):
        for j in range(1, 256, 1):
            for k in range(1, 256, 1):

                # Find the value of 2 * s
                peri = i + j + k

                # Find the value of
                # 2 * ( s - a )
                mul1 = -i + j + k
                if (k > 100):
                  break
                if (j > 100):
                  break
                if (i > 100):
                  break

                # Find the value of
                # 2 * ( s - b )
                mul2 = i - j + k

                # Find the value of
                # 2 * ( s - c )
                mul3 = i + j - k

                # If triplets have same
                # area and perimeter
                if (16 * peri == mul1 * mul2 * mul3):

                    # Store sides of triangle
                    v =  [i, j, k]

                    # Sort the triplets
                    v.sort(reverse = False)

                    # Inserting in set to
                    # avoid duplicate sides
                    se.append(v)
                    se.sort(reverse = False)

    # Print sides of all desired triangles
    temp = []
    temp.append(se[0])
    temp.append(se[6])
    temp.append(se[12])
    temp.append(se[18])
    temp.append(se[24])
    for it in temp:
        print(it[0], it[1], it[2])

# Driver Code
if __name__ == '__main__':

    # Function call
    samePerimeterAndArea()

# This code is contributed by ipg2016107

C#

// C# program for the above approach
using System;
using System.Collections.Generic;

public class GFG {

  // Function to print sides of all the
  // triangles having same perimeter & area
  static void samePerimeterAndArea()
  {

    // Stores unique sides of triangles
    HashSet<Tuple<int, int, int>> se = new HashSet<Tuple<int, int, int>>();

    // i + j + k values cannot exceed 256
    for (int i = 1; i <= 256; ++i) {

      for (int j = 1; j <= 256; ++j) {

        for (int k = 1; k <= 256; ++k) {

          // Find the value of 2 * s
          int peri = i + j + k;

          // Find the value of
          // 2 * ( s - a )
          int mul1 = -i + j + k;

          // Find the value of
          // 2 * ( s - b )
          int mul2 = i - j + k;

          // Find the value of
          // 2 * ( s - c )
          int mul3 = i + j - k;

          // If triplets have same
          // area and perimeter
          if (16 * peri == mul1 * mul2 * mul3) {

            // Store sides of triangle
            List<int> v=new List<int>();
            v.Add(i);
            v.Add(j);
            v.Add(k);

            // Sort the triplets
            v.Sort();

            // Inserting in set to
            // avoid duplicate sides
            Tuple<int, int, int> t = Tuple.Create(v[0], v[1], v[2]);
            se.Add(t);
          }
        }
      }
    }

    // Print sides of all desired triangles
    foreach (var it in se) {
      Console.WriteLine(String.Join(" ", it));
    }
  }

  // Driver Code
  public static void Main(string[] args)
  {

    // Function Call
    samePerimeterAndArea();
  }
}

// The code is contributed by phasing17

Javascript

<script>

// JavaScript program for the above approach

// Function to print sides of all the
// triangles having same perimeter & area
const samePerimeterAndArea = () => {

    // Stores unique sides of triangles
    let se = [];

    // i + j + k values cannot exceed 256
    for(let i = 1; i <= 256; ++i)
    {
        for(let j = 1; j <= 256; ++j)
        {
            for(let k = 1; k <= 256; ++k)
            {

                // Find the value of 2 * s
                let peri = i + j + k;

                // Find the value of
                // 2 * ( s - a )
                let mul1 = -i + j + k;

                // Find the value of
                // 2 * ( s - b )
                let mul2 = i - j + k;

                // Find the value of
                // 2 * ( s - c )
                let mul3 = i + j - k;

                // If triplets have same
                // area and perimeter
                if (16 * peri == mul1 * mul2 * mul3)
                {

                    // Store sides of triangle
                    let v = [i, j, k];

                    // Sort the triplets
                    v.sort((a, b) => a - b);

                    // Inserting in se to check
                    // avoid duplicate sides
                    let check = -1;
                    for(let i = 0; i < se.length; ++i)
                    {
                        if (se[i][0] == v[0] &&
                            se[i][1] == v[1] &&
                            se[i][2] == v[2])
                            check = 1;
                    }
                    if (check === -1) se.push(v);
                }
            }
        }
    }

    // Print sides of all desired triangles
    for(let it = 0; it < se.length; ++it)
    {
        document.write(`${se[it]}<br/>`);
    }
}

// Driver Code

// Function call
samePerimeterAndArea();

// This code is contributed by rakeshsahni

</script>

Output:

5 12 13
6 8 10
6 25 29
7 15 20
9 10 17

Time Complexity: O(256³)
Auxiliary Space: O(256³)