When two or more than two solids are combined and the combination comes out useful, a shape that can be found in reality is called a combination of solids. When Solids are taught, the major focus is always on the point of their real-life use and applications, For example, a cylinder can be seen in Pipes or even in small objects like batteries, a sphere is a ball (from football to a tennis ball), a pyramid or a tent are in the shape of a cone, a book is in the shape of a cuboid, etc. Similarly, Combining these solids also gives new shapes that are often found and seen in real life.
Let’s learn about the basic shapes and their Volumes in details
Cuboid
When 6 rectangles figures are combined, to form a closed three-dimensional figure, a cuboid is obtained. A Cuboid can also be imagined as a three-dimensional rectangle, that is, adding multiple rectangles on top of each other (rectangles have to be of the same size) and making it big enough to have some height will give a cuboid.
- A cuboid has 6 faces
- A cuboid has 12 edges
Volume of a Cuboid = L× B× H

Cube
A cube is formed by combining 6 squares of equal size in a 3-D figure. Similarly, like a cuboid, a cube can also be defined as multiple similar squares on top of each other forming some height to the planar figure.
- A cube has 6 faces
- A cube has 12 edges.
Volume of a Cube = a × a × a = a3

Cylinder
A cylinder, mostly known as the basic curved 3-D figure we study about, a Cylinder has its curved surface formed by a fixed point known as the axis. A cylinder can also be denoted as multiple circles on top of each other giving it a visible height.
Volume of a Cylinder= πr2h
Where, r= radius of the base of cylinder
h= height of the cylinder

Cone
A Cone is a 3-D figure having a circular base and the height goes tapered from bottom to top meeting at a point on top known as vertex or apex. A cone shape is very commonly seen in daily life, for example, a tent formed is in the shape of a cone, an icecream cone has a cone in its name itself and the shape is conical too.
Volume of Cone = 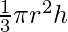
Here, r = radius of the base of cone
h = height of the cone
l = slant height of cone (shown in figure)

Sphere
A three-dimensional shape in which the entire periphery is equidistant from a fixed point is a sphere. A sphere can be called as a 3-D circle. Example of a sphere is the shape of a globe, moon, ball, etc. The significance of a sphere not only exists in maths but goes as far as in astrophysics.
Volume of a Sphere = 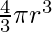
r = radius of the sphere.

Hemisphere
We very often hear terms like Northern Hemisphere and Southern Hemisphere while studying geography, the terms are associated with half of the globe. Similarly, imagine cutting a sphere in half, the two 3-D shapes obtained are Hemispherical shapes. So, a hemisphere is half as a sphere and so is the formula for the volume of a hemisphere.
Volume of a Hemisphere = 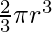
r = radius of the base of hemisphere

Combination of Solids
So far, the simple and basic solid shapes that exist were discussed. However, there are various cases where these basic shapes are combined to form a whole new shape and that shape would have its own unique features that are the combined features of separate shapes. For example, What will happen when we combine two cubes? It will give us a cuboid, The icecream is not but the combination of a cone and a Hemisphere, The shape of a Hut is a combination of cylinder and Cone, Likewise, there are many more real-life examples to exist.
Examples of combination of solids

An Icecream Cone

A Hut
Volume of the combination of Solids
The volume of any combination of solid is nothing but the summation of separate solids that are combined to form that shape, For instance, ice cream is a combination of a cone and a hemisphere, therefore, the volume of the ice cream will be the combined volume of cone and the hemisphere., that is, 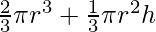
Sample Problems on Combinations of solids
Question 1: Two cubes of equal edges, 2cm, are joined side by side to form a cuboid. What is the Volume of this new cuboid formed?
Solution:
When two cubes are joined side by side, the length will double but the height and the breadth of the cuboid will be equal to the side of the cube.

Therefore, Volume of the cuboid will be,
Volume= L× B× H
= 2× 2× 4= 16cm3
Question 2: A container is in the shape of a cylinder and the container’s lid is in the shape of a hollow hemisphere which fits the container perfectly. The radius of the base of the cylinder is 21cm and the height of the cylinder is 50 cm. Find out the volume of the container when the lid is closed.
Solution:
The shape of the container with the lid closed shall look something like this,

The radius of the base of hemisphere will be equal to the radius of the cylinder.
The volume of container= Volume of Hemisphere+ Volume of cylinder
= 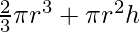
= 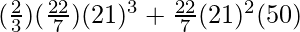
=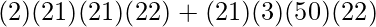
= 88704cm3
Question 3: There are multiple smaller cube, each having an edge of 2cm are placed together to form a bigger cube of side length 8cm, How many smaller cubes are required to form the bigger cube?
Solution:
lets say that there are n number of cubes required to form the bigger cube, the volume of the bigger cube and n number of cubes will remain same.
n (2)3= (8)3
n (2× 2× 2)= 8× 8× 8
n = 64 cubes.
Question 4: A Toy is in the shape of a hemisphere with a cone on top of it, the diameter of the hemisphere is equal to the diameter of the base of cone, d= 14cm. The height of the toy is 28cm. Find the Volume of the toy.
Solution:
The toy should look something like this,

The radius of the cone and hemisphere = 7cm
The height of the Cone= 28 – 7= 21cm
Volume of the Toy= Volume of the hemisphere + Volume of the Cone
= 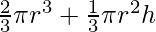
=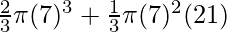
= 718.37 +1077.56
= 1795.93 cm3
Question 5: A Sphere has hollowed by embedding another sphere of half the radius, Find the volume of the remaining sphere. The figure is shown below.

Solution:
The larger sphere has the diameter=28cm
Radius of the Larger sphere (R)= 28/2= 14cm
Radius of the smaller sphere (r) = 14/2= 7cm
Volume of the remaining Hollow sphere= Volume of larger sphere- Volume of smaller sphere.
= 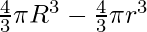
=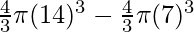
= 10060cm3
Share your thoughts in the comments
Please Login to comment...