Conversion of solids – Surface Areas and Volumes
Last Updated :
21 Nov, 2022
Conversions or changes are now a normal feature of our everyday lives. A goldsmith, for instance, melts a strip of gold to turn it into a gem. Likewise, a kid plays with clay forms it into various toys, a carpenter uses the wooden logs to shape various items/furniture for housekeeping. Likewise, for different purposes, the conversion of solids from one form to another is necessary. Each and every solid that exists occupies some volume. No matter how distinctive the new shape is, as you transform one solid shape to another, the volume stays the same. In fact, if you melt one large candle into ten small candles, the sum of the volume of the smaller candles would be equal to the volume of the larger candles. In this section, we will see some problems related to it.
Sample Problems on Conversion of Solids
Example 1: A silver sphere ball of radius 10 cm is melted and recast into small spheres each of radius 5 cm so that children can play. How many small spheres can be obtained?
Solution:
Say the number of small spheres obtained be x.
We know that the total volume will remain the same.
R = 10 cm (Radius of the big ball).
r = 5 cm (radius of the small ball).
Now, n × (Volume of a small ball) = Volume of a big metallic ball
x * (4/3) * π * r3 = (4/3) * π * R3
Hence we get: x = 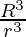
Therefore x is 8. Hence we can make 8 small balls out of 1 big ball.
Example 2: We have a cylindrical candle, 14 cm in diameter and of length 2cm. It is melted to form a cuboid candle of dimensions 7 cm × 11 cm×1 cm. How many Cuboidal candles can be obtained?
Solution:
Dimensions of the cylindrical Candle:
Radius of cylindrical candle = 14/2 cm = 7 cm
Height/Thickness = 2 cm
Volume of one cylindrical candle = πr2h = π x 7 x 7 x (2) cm3 = 308 cm3
Volume of cuboid candle = 7 x 11 x 1 = 77 cm3
Hence, the number of Cuboidal candles = Volume of cuboid candle/Volume of one cylindrical candle = 308/77 = 4. Hence we can get 4 Cuboidal shaped candles.
Example 3: We are given a cone made up of clay of height 30 cm. We have to make it in the shape of a cylinder of the same radius. Find the height of the cylinder?
Solution :
Let h1 and h2 be the heights of a cylinder and cone respectively. Let r be the radius of the cone and also the radius of the cylinder as given in the question.
As we know that:
The volume of cylinder = Volume of cone.
πr2h1 = (1/3) πr2h2
h2 = 30 cm
h1= (30/3) = 10 cm
Therefore, the height of the cylinder is 10 cm
Example 4: A cylindrical copper rod with a diameter of 2 cm and length of 2 cm is drawn into a wire of length 72 m of uniform thickness. Determine the thickness of the wire?
Solution:
Given that, the diameter of the Copper rod = 2 cm.
Radius = 1 cm.
Length of the copper rod = 2 cm
The volume of the copper Cylindrical material = π × (1)2 × 2 = 2π cm3
Length of new wire = 72 m = 18 × 100 = 7200 cm.
We know that the wire should be in a cylindrical shape.
If “r” is the radius of the cross-section of the wire, then the volume of the wire is given as:
The volume of the wire = π × r2 × 7200
Since the volume of the copper rod and the volume of the new wire should be equal, then we can write
⇒ π × r2 × 7200 = 2π
⇒ r = 1/60 cm.
Hence, the thickness of the wire should be the diameter of the cross-section of the new wire.
Thickness = (1/60) x 2 = 1/30 cm. Thus, the thickness of the wire is approximately equal to 0.0334 cm.
Share your thoughts in the comments
Please Login to comment...