Queue Notes for GATE Exam [2024]

A Queue is defined as a linear data structure that is open at both ends and the operations are performed in First In First Out (FIFO) order. Queue is a list in which all additions to the list are made at one end, and all deletions from the list are made at the other end.  The element, which is first pushed into the order, the operation is first performed on that.

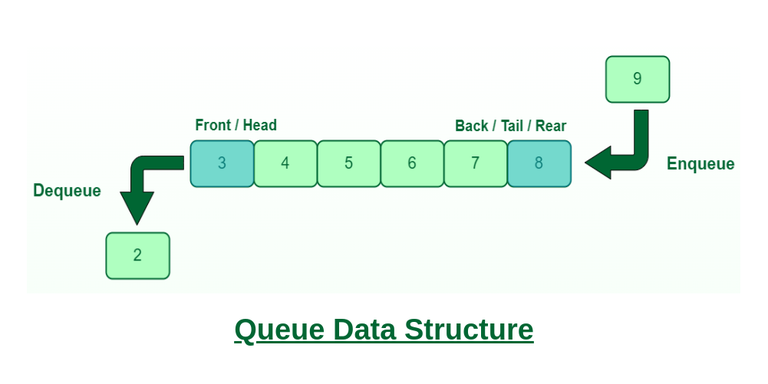
FIFO Property in Queue

Implementing Queues using Arrays:

To implement a queue using an array, 

• Create an array arr of size n and 
• Take two variables front and rear both of which will be initialized to 0 which means the queue is currently empty. 
• Element 
  • rear is the index up to which the elements are stored in the array and 
  • front is the index of the first element of the array.

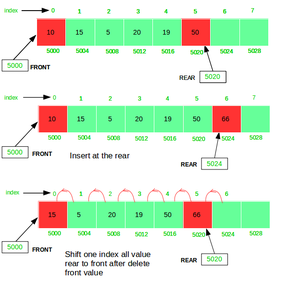
Now, some of the implementations of queue operations are as follows: 

• Enqueue: Addition of an element to the queue. Adding an element will be performed after checking whether the queue is full or not. If rear < n which indicates that the array is not full then store the element at arr[rear] and increment rear by 1 but if rear == n then it is said to be an Overflow condition as the array is full. Enqueue has O(1) time complexity.
• Dequeue: Removal of an element from the queue. An element can only be deleted when there is at least an element to delete i.e. rear > 0. Now, the element at arr[front] can be deleted but all the remaining elements have to shift to the left by one position in order for the dequeue operation to delete the second element from the left on another dequeue operation. Dequeue has O(N) time complexity.
• Front: Get the front element from the queue i.e. arr[front] if the queue is not empty. Accessing the front of the queue has O(1) time complexity.
• Display: Print all elements of the queue. If the queue is non-empty, traverse and print all the elements from the index front to rear. Displaying all the elements has O(N) time complexity.
• Overall Space Complexity: O(N)

Implementing Queues using Linked List:

To implement a queue using a Linked List,

• Maintain two pointers, front and rear. The front points to the first item of the queue and rear points to the last item.
  • enQueue(): This operation adds a new node after the rear and moves the rear to the next node.
  • deQueue(): This operation removes the front node and moves the front to the next node.

Now, some of the implementations of queue operations are as follows: 

• Create a class QNode with data members integer data and QNode* next (pointer to the next node)
• Create a class Queue with data members QNode front and rear
• Enqueue Operation with parameter x:
  • Initialize QNode* temp with data = x
  • If the rear is set to NULL then set the front and rear to temp and return (Base Case)
  • Else set rear next to temp and then move rear to temp
  • Enqueue has O(1) time complexity.
• Dequeue Operation:
  • If the front is set to NULL return (Base Case)
  • Initialize QNode temp with front and set front to its next
  • If the front is equal to NULL then set the rear to NULL
  • Delete temp from the memory.
  • Dequeue has O(1) time complexity.
• Overall Space Complexity: O(N)

Implementation of Queue using Stack:

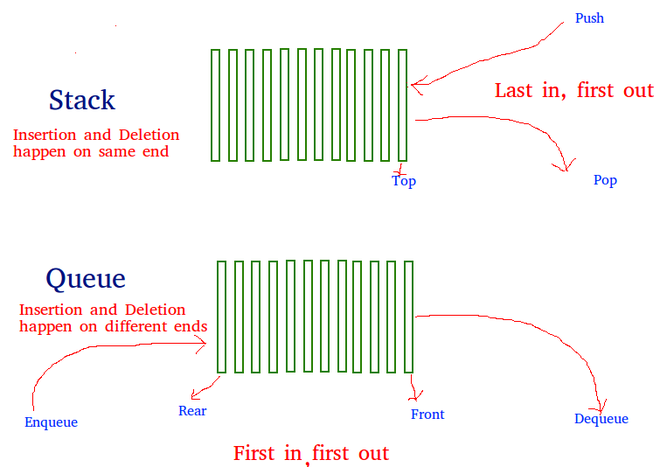
A queue can be implemented using two stacks. Let queue to be implemented be q and stacks used to implement q be stack1 and stack2. q can be implemented in three ways: 

Method 1 (By making enQueue operation costly): This method makes sure that oldest entered element is always at the top of stack 1, so that deQueue operation just pops from stack1. To put the element at top of stack1, stack2 is used.

enQueue(q, x): 

• While stack1 is not empty, push everything from stack1 to stack2.
• Push x to stack1 (assuming size of stacks is unlimited).
• Push everything back to stack1.
• Time complexity will be O(N).

deQueue(q): 

• If stack1 is empty, then error
• Pop an item from stack1 and return it.
• Time complexity will be O(1).

Method 2 (By making deQueue operation costly): In this method, in en-queue operation, the new element is entered at the top of stack1. In de-queue operation, if stack2 is empty then all the elements are moved to stack2 and finally top of stack2 is returned. 

enQueue(q, x):

• Push x to stack1 (assuming size of stacks is unlimited).
• Time complexity will be O(1)

deQueue(q):

• If both stacks are empty then error.
• If stack2 is empty, while stack1 is not empty, push everything from stack1 to stack2.
• Pop the element from stack2 and return it.
• Time complexity will be O(N)

Method 2 is definitely better than method 1. Method 1 moves all the elements twice in enQueue operation, while method 2 (in deQueue operation) moves the elements once and moves elements only if stack2 empty. So, the amortized complexity of the dequeue operation becomes Θ(1)

Method 3 (Using one user stack and one function call stack):  Method 2 can be modified where recursion (or Function Call Stack) is used to implement queue using only one user defined stack.

enQueue(x):

• Push x to stack1.
• Time complexity will be O(1)

deQueue():

• If stack1 is empty, then error.
• If stack1 has only one element, then return it.
• Recursively pop everything from the stack1, store the popped item in variable res, push the res back to stack1 and return res.
• Time Complexity will be O(N).

Circular Queue:

A Circular Queue is an extended version of a normal queue where the last element of the queue is connected to the first element of the queue forming a circle. The operations are performed based on FIFO (First In First Out) principle. It is also called ‘Ring Buffer’. 

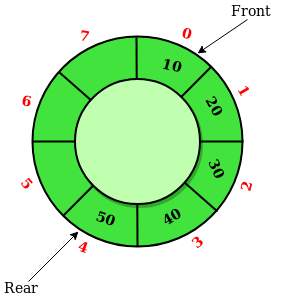
Operations on Circular Queue:

• Front: Get the front item from the queue. Accessing the front element has O(1) time complexity.
• Rear: Get the last item from the queue. Accessing the rear element has O(1) time complexity.
• enQueue(value): This function is used to insert an element into the circular queue. In a circular queue, the new element is always inserted at the rear position. 
  • Check whether the queue is full – [i.e., the rear end is in just before the front end in a circular manner].
  • If it is full then display Queue is full, else insert an element at the end of the queue.
  • The time complexity is O(1).
• deQueue(): This function is used to delete an element from the circular queue. In a circular queue, the element is always deleted from the front position. 
  • Check whether the queue is Empty.
  • If it is empty, then display Queue is empty, else get the last element and remove it from the queue.
  • The Time Complexity is O(1).

Applications of Circular Queue:

• In a page replacement algorithm, a circular list of pages is maintained and when a page needs to be replaced, the page in the front of the queue will be chosen.
• Computer systems supply a holding area for maintaining communication between two processes or two programs. This memory area is also known as a ring buffer.
• CPU Scheduling: In the Round-Robin scheduling algorithm, a circular queue is utilized to maintain processes that are in a ready state.

Priority Queue:

A priority queue is a type of queue that arranges elements based on their priority values. Elements with higher priority values are typically retrieved before elements with lower priority values.
If we add an element with a high priority value to a priority queue, it may be inserted near the front of the queue, while an element with a low priority value may be inserted near the back.

Types of Priority Queue:

• Descending Order Priority Queue Max Heap: Higher Priority values are given more priority as compared to Lower Priority values.
• Ascending Order Priority Queue or Min Heap: Lower Priority values are given more priority as compared to Higher Priority values.

Properties of Priority Queue:

• Every item has a priority associated with it.
• An element with high priority is dequeued before an element with low priority.
• If two elements have the same priority, they are served according to their order in the queue.

In the below priority queue, an element with a maximum ASCII value will have the highest priority. The elements with higher priority are served first. 

Operations on Priority Queue:

• Insertion in a Priority Queue: When a new element is inserted in a priority queue, it is placed after the last element and is swapped with the parent node if the order is incorrect. The swapping process continues until all the elements are placed in the correct position. The time complexity is O(logN), where N is the number of elements in the priority queue.
• Deletion in a Priority Queue: It will remove the element which has maximum priority first. This removal creates an empty slot, which will be further filled with new insertion. Then, it compares the newly inserted element with all the elements inside the queue to maintain the heap invariant. The time complexity is O(logN), where N is the number of elements in the priority queue.
• Peek in a Priority Queue: This operation helps to return the maximum element from Max Heap or the minimum element from Min Heap without deleting the node from the priority queue. The time complexity is O(1).

Applications of Priority Queue:

• Dijkstra’s Shortest Path Algorithm using priority queue: When the graph is stored in the form of adjacency list or matrix, priority queue can be used to extract minimum efficiently when implementing Dijkstra’s algorithm. 
• Prim’s algorithm: It is used to implement Prim’s Algorithm to store keys of nodes and extract minimum key node at every step.
• The priority queue (also known as the fringe) is used to keep track of unexplored routes, the one for which a lower bound on the total path length is smallest is given highest priority. 
• Heap Sort: Heap sort is typically implemented using Heap which is an implementation of Priority Queue. 
• Operating systems: It is also used in Operating System for load balancing (load balancing on server), >interrupt handling. 

Double Ended Queue:

Deque or Double Ended Queue is a generalized version of Queue data structure that allows insert and delete at both ends.

Operations on Double Ended Queue:

• Front: Get the front item from the deque. Accessing the front element has O(1) time complexity.
• Rear: Get the last item from the deque. Accessing the rear element has O(1) time complexity.
• push_front(x): Inserts the element x at beginning of the deque. Time Complexity is O(1).
• push_back(x): Inserts the element x at the back of the deque. Time Complexity is O(1).
• pop_front(): Removes the first element from the deque. Time Complexity is O(1).
• pop_back(): Removes the last element from the deque. Time Complexity is O(1).

Applications of Double Ended Queue:

• Used in Job scheduling algorithms.
• In a web browser’s history, recently visited URLs are added to the front of the deque and the URL at the back of the deque is removed after some specified number of operations of insertions at the front.
• Storing a software application’s list of undo and redo operations.
• In caching systems to cache frequently accessed data. Deques can be used to store cached data and efficiently support operations such as adding or removing data from both ends of the deque.

GATE Archives – Previous Years Questions on Queue:

Q1. Following is C like pseudo-code of a function that takes a Queue as an argument, and uses a stack S to do processing. 

C

void fun(Queue *Q)
{
    Stack S;  // Say it creates an empty stack S

    // Run while Q is not empty
    while (!isEmpty(Q))
    {
        // deQueue an item from Q and push the dequeued item to S
        push(&S, deQueue(Q));
    }

    // Run while Stack S is not empty
    while (!isEmpty(&S))
    {
      // Pop an item from S and enqueue the popped item to Q
      enQueue(Q, pop(&S));
    }
}

What does the above function do in general?

(A) Removes the last from Q

(B) Keeps the Q same as it was before the call

(C) Makes Q empty

(D) Reverses the Q

Answer: (D)
Explanation: The function takes a queue Q as an argument. It dequeues all items of Q and pushes them to a stack S. Then pops all items of S and enqueues the items back to Q. Since the stack is LIFO order, all items of the queue are reversed.
Hence option (D) is the correct answer.

Q2. Which one of the following is an application of Queue Data Structure?

(A) When a resource is shared among multiple consumers.

(B) When data is transferred asynchronously (data not necessarily received at same rate as sent) between two processes

(C) Load Balancing

(D) All of the above

Answer: (D)
Explanation:
(A) When a resource is shared among multiple consumers: In scenarios where a resource (such as a printer, CPU time, or database connection) needs to be shared among multiple consumers or processes, a queue data structure can be used. Each consumer can enqueue their requests for the resource, and the resource can be allocated to them in the order of their requests by dequeuing from the queue. This ensures fair access to the shared resource and prevents conflicts or resource contention.

(B) When data is transferred asynchronously between two processes: When data is transferred asynchronously between two processes or systems, a queue can be used as a buffer or intermediary storage. One process enqueues the data to be sent, while the other process dequeues and processes the received data. The queue allows for decoupling the rate of data production from data consumption, ensuring smooth and efficient communication between the processes.

(C) Load Balancing: Load balancing is the practice of distributing workloads across multiple resources to optimize performance and utilization. A queue data structure can be used in load-balancing algorithms to manage incoming requests or tasks. The requests are enqueued in the queue, and the load balancer can dequeue and assign them to available resources based on various criteria (e.g., round-robin, least connections). This helps distribute the workload evenly across the resources, preventing overload and maximizing throughput.

Q3. How many stacks are needed to implement a queue. Consider the situation where no other data structure like arrays, linked list is available to you.

(A) 1

(B) 2

(C) 3

(D) 4

Answer: (B)
Explanation: A queue can be implemented using two stacks. Refer this for more reference: https://www.geeksforgeeks.org/queue-using-stacks/
Hence Option(B) is the correct answer.

Q4. How many queues are needed to implement a stack. Consider the situation where no other data structure like arrays, linked list is available to you.

(A) 1

(B) 2

(C) 3

(D) 4

Answer: (B)
Explanation: A stack can be implemented using two queues. Refer this for more reference: https://www.geeksforgeeks.org/implement-stack-using-queue/
Hence Option(B) is the correct answer.

Q5. Which of the following is true about linked list implementation of queue?

(A) In push operation, if new nodes are inserted at the beginning of linked list, then in pop operation, nodes must be removed from end.

(B) In push operation, if new nodes are inserted at the end, then in pop operation, nodes must be removed from the beginning.

(C) Both of the above

(D) None of the above

Answer: (C)
Explanation: To keep the First In First Out order, a queue can be implemented using a linked list in any of the given two ways.
Hence option (C) is the correct answer.

Q6. Suppose a circular queue of capacity (n – 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operation are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are

(A) Full: (REAR+1) mod n == FRONT, empty: REAR == FRONT

(B) Full: (REAR+1) mod n == FRONT, empty: (FRONT+1) mod n == REAR

(C) Full: REAR == FRONT, empty: (REAR+1) mod n == FRONT

(D) Full: (FRONT+1) mod n == REAR, empty: REAR == FRONT

Answer: (A)
Explanation: Suppose we start filling the queue.
Let the maxQueueSize ( Capacity of the Queue) is 4.So the size of the array which is used to implement this circular queue is 5, which is n. In the beginning when the queue is empty, FRONT and REAR point to 0 index in the array. REAR represents insertion at the REAR index. FRONT represents deletion from the FRONT index.
enqueue(“a”); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 1)
enqueue(“b”); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 2)
enqueue(“c”); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 3)
enqueue(“d”); REAR = (REAR+1)%5; ( FRONT = 0, REAR = 4)
Now the queue size is 4 which is equal to the maxQueueSize. Hence overflow condition is reached.
Now, we can check for the conditions.
When Queue Full :
( REAR+1)%n = (4+1)%5 = 0
FRONT is also 0. Hence ( REAR + 1 ) %n is equal to FRONT.
When Queue Empty :
REAR was equal to FRONT when empty ( because in the starting before filling the queue FRONT = REAR = 0 )
Hence Option A is correct. 

Q7. Consider the following pseudo code. Assume that IntQueue is an integer queue. What does the function fun do? 

C

void fun(int n)
{
    IntQueue q = new IntQueue();
    q.enqueue(0);
    q.enqueue(1);
    for (int i = 0; i < n; i++) {
        int a = q.dequeue();
        int b = q.dequeue();
        q.enqueue(b);
        q.enqueue(a + b);
        print(a);
    }
}

(A) Prints numbers from 0 to n-1

(B) Prints numbers from n-1 to 0

(C) Prints first n Fibonacci numbers

(D) Prints first n Fibonacci numbers in reverse order.

Answer: (C)
Explanation: The function prints first n Fibonacci Numbers. Note that 0 and 1 are initially there in q. In every iteration of the loop sum of the two queue items is enqueued and the front item is dequeued.
Hence option (C) is the correct answer.

Q8. Which of the following is NOT a common operation in a queue data structure? 

(A) Enqueue

(B) Dequeue

(C) Peak

(D) Shuffle

Answer: (D)
Explanation: Shuffle is NOT a common operation in a queue data structure.
Hence Option (D) is the correct answer.

Q9. Suppose a stack implementation supports an instruction REVERSE, which reverses the order of elements on the stack, in addition to the PUSH and POP instructions. Which one of the following statements is TRUE with respect to this modified stack?

(A) A queue cannot be implemented using this stack.

(B) A queue can be implemented where ENQUEUE takes a single instruction and DEQUEUE takes a sequence of two instructions.

(C) A queue can be implemented where ENQUEUE takes a sequence of three instructions and DEQUEUE takes a single instruction.

(D) A queue can be implemented where both ENQUEUE and DEQUEUE take a single instruction each.

Answer: (C)
Explanation: To DEQUEUE an item, simply POP. To ENQUEUE an item, we can do following 3 operations 1) REVERSE 2) PUSH 3) REVERSE
Hence Option (C) is the correct answer.

Q10. A queue is implemented using an array such that ENQUEUE and DEQUEUE operations are performed efficiently. Which one of the following statements is CORRECT (n refers to the number of items in the queue)?

(A) Both operations can be performed in O(1) time

(B) At most one operation can be performed in O(1) time but the worst case time for the other operation will be Ω(n)

(C) The worst case time complexity for both operations will be Ω(n)

(D) Worst case time complexity for both operations will be Ω(log n)

Answer: (A)
Explanation: We can use circular array to implement both in O(1) time. See below article for details
Queue Introduction and Array Implementation
Hence Option (D) is the correct answer.