Data Structures and Algorithms | Set 26
Last Updated :
13 Dec, 2022
Following questions have been asked in GATE 2011 exam.
1) A max-heap is a heap where the value of each parent is greater than or equal to the values of its children. Which of the following is a max-heap?
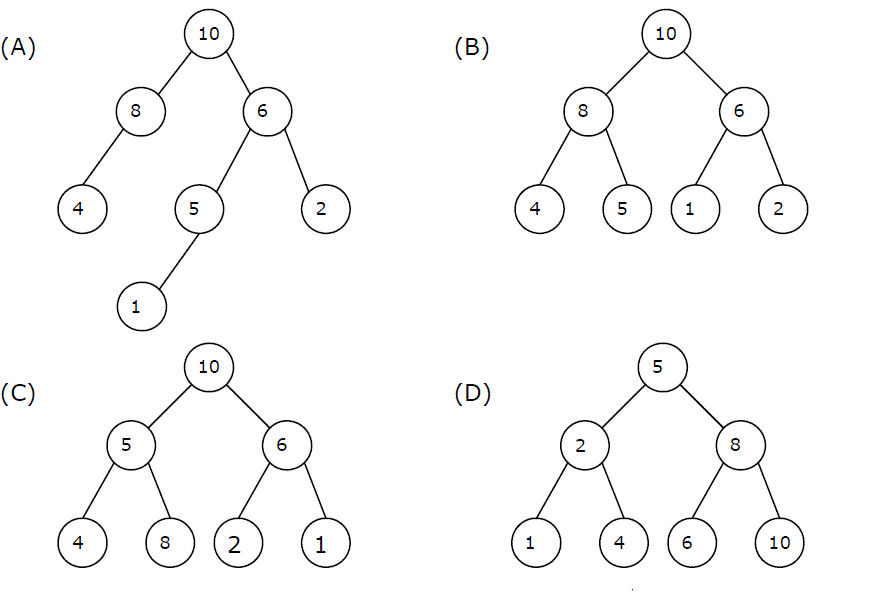
Answer: (B)
A binary tree is max-heap if it is a complete binary tree (A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible) and it follows the max-heap property (value of each parent is greater than or equal to the values of its children).
A) is not a max-heap because it is not a complete binary tree
B) is a max-heap because it is complete binary tree and follows max-heap property.
C) is not a max-heap because 8 is a chile of 5 in this tree, so violates the max-heap property.
D) is not a max-heap because 8 is a chile of 5 in this tree, so violates the max-heap property. There are many other nodes in this tree which violate max-heap property in this tree.
2) Four matrices M1, M2, M3 and M4 of dimensions pxq, qxr, rxs and sxt respectively can be multiplied is several ways with different number of total scalar multiplications. For example, when multiplied as ((M1 X M2) X (M3 X M4)), the total number of multiplications is pqr + rst + prt. When multiplied as (((M1 X M2) X M3) X M4), the total number of scalar multiplications is pqr + prs + pst.
If p = 10, q = 100, r = 20, s = 5 and t = 80, then the number of scalar multiplications needed is
A) 248000
B) 44000
C) 19000
D) 25000
Answer (C)
We get minimum number of multiplications using ((M1 X (M2 X M3)) X M4).
Total number of multiplications = 100x20x5 (for M2 x M3) + 10x100x5 + 10x5x80 = 19000.
3) Which of the given options provides the increasing order of asymptotic complexity of functions f1, f2, f3 and f4?
f1(n) = 2^n
f2(n) = n^(3/2)
f3(n) = nLogn
f4(n) = n^(Logn)
A) f3, f2, f4, f1
B) f3, f2, f1, f4
C) f2, f3, f1, f4
D) f2, f3, f4, f1
Answer (A)
See https://www.geeksforgeeks.org/algorithms-analysis-of-algorithms-question-9/ for explanation.
4) We are given a set of n distinct elements and an unlabeled binary tree with n nodes. In how many ways can we populate the tree with the given set so that it becomes a binary search tree?
A) 0
B) 1
C) n!
D) (1/(n+1)).2nCn
Answer (B)
See this explanation from PeddaBoku.
5) An algorithm to find the length of the longest monotonically increasing sequence of numbers in an array A[0 :n-1] is given below.
Let Li denote the length of the longest monotonically increasing sequence starting at index i in the array

Which of the following statements is TRUE?
(A) The algorithm uses dynamic programming paradigm
(B) The algorithm has a linear complexity and uses branch and bound paradigm
(C) The algorithm has a non-linear polynomial complexity and uses branch and bound paradigm
(D) The algorithm uses divide and conquer paradigm.
Answer: (A)
Please see GATE Corner for all previous year paper/solutions/explanations, syllabus, important dates, notes, etc.
Please write comments if you find any of the answers/explanations incorrect, or you want to share more information about the topics discussed above.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...