Divide and Conquer Notes for GATE Exam [2024]

Those preparing for the GATE (Graduate Aptitude Test in Engineering) exam in 2024 face many algorithmic challenges. Among the various algorithmic paradigms, “Divide and Conquer” stands out as a powerful approach to problem-solving. In this comprehensive guide for the GATE Exam, Divide and Conquer, and its applications will be explored through a range of important topics. These notes aim to provide a solid foundation for mastering these concepts in preparation for the upcoming GATE exam.

Introduction to Divide and Conquer:

Divide and Conquer is an algorithmic paradigm in which the problem is solved using the Divide, Conquer, and Combine strategy.

A typical Divide and Conquer algorithm solves a problem using following three steps:

1. Divide: This involves dividing the problem into smaller sub-problems.
2. Conquer: Solve sub-problems by calling recursively until solved.
3. Combine: Combine the sub-problems to get the final solution of the whole problem.

Below are different algorithms which are based on Divide and Conquer:

Application of Divide & Conquer in Binary Search:

Binary Search is a search algorithm that efficiently finds a target value within a sorted array. It repeatedly divides the search space in half until the target is found or the search space is empty.

Algorithm Steps:

• Initialize low, high, and mid indices.
• Compare the target with the element at the mid index.
• If the target is found, return the index.
• If the target is smaller, update the high index to mid – 1.
• If the target is larger, update the low index to mid + 1.
• Repeat the process until the target is found or the search space is empty.

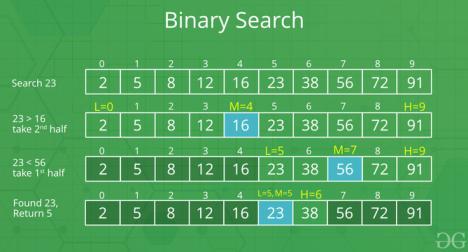
Binary Search

Application of Divide & Conquer in Merge Sort:

Merge Sort is a divide-and-conquer sorting algorithm that recursively divides an array into two halves, sorts each half, and then merges them to produce a sorted array.

Algorithm Steps:

• Divide the unsorted array into two halves.
• Recursively apply Merge Sort to each half.
• Merge the sorted halves to produce a sorted array.

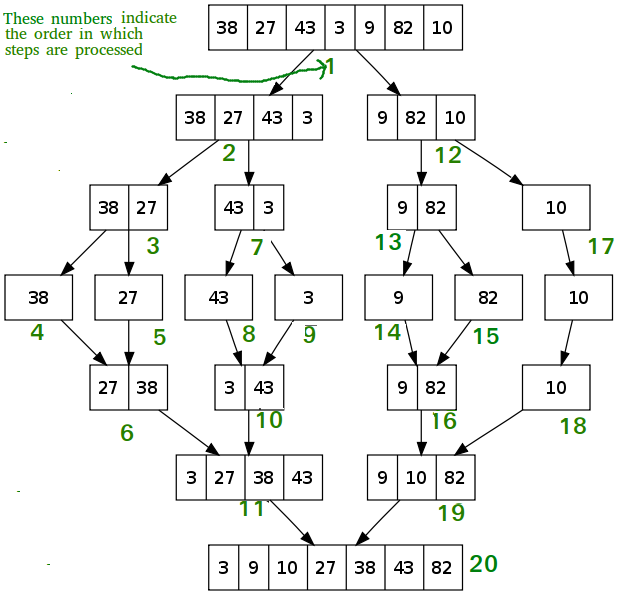
Time Complexity:

• Worst Case: O(n log n)
• Best Case: O(n log n)
• Average Case: O(n log n)

Space Complexity: O(n), additional space for the temporary array used in the merge step.

Application of Divide & Conquer in Quick Sort:

QuickSort is a sorting algorithm based on the Divide and Conquer algorithm that picks an element as a pivot and partitions the given array around the picked pivot by placing the pivot in its correct position in the sorted array.

The key process in quickSort is a partition(). The target of partitions is to place the pivot (any element can be chosen to be a pivot) at its correct position in the sorted array and put all smaller elements to the left of the pivot, and all greater elements to the right of the pivot.
Partition is done recursively on each side of the pivot after the pivot is placed in its correct position and this finally sorts the array.

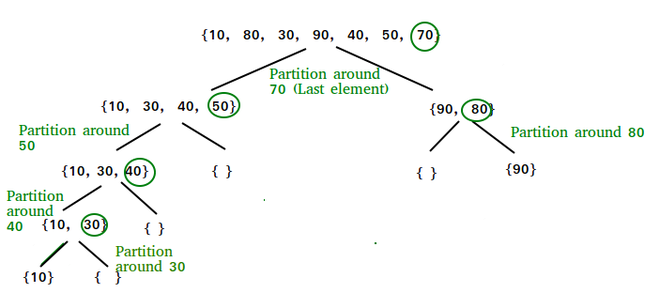
Choice of Pivot:

There are many different choices for picking pivots. 

• Always pick the first element as a pivot.
• Always pick the last element as a pivot
• Pick a random element as a pivot.
• Pick the middle as the pivot.

Time Complexity:

• Worst Case: O(n^2), occurs when the pivot selection consistently results in unbalanced partitions.
• Best Case: O(n log n), occurs when the pivot selection consistently results in balanced partitions.
• Average Case: O(n log n)

Space Complexity: O(log n), for the recursive call stack.

Standard Problems that uses Divide and Conquer Algorithm:

1. Merge Sort for Linked List:

Merge Sort can be adapted for linked lists. It follows the same divide-and-conquer approach, dividing the linked list into two halves, recursively sorting each half, and then merging them.

Algorithm Steps:

• If the list is empty or has one element, it is already sorted.
• Split the linked list into two halves.
• Recursively sort each half.
• Merge the sorted halves.

2. How to make Merge Sort to perform O(n) comparisons in best case?

Optimizing Merge Sort to perform O(n) comparisons in the best case involves detecting if the input is already sorted and skipping unnecessary merging steps.

Algorithm Steps:

• Check if the input is already sorted.
• If sorted, skip merging and return the sorted array.
• Otherwise, proceed with the standard Merge Sort algorithm.

3. Iterative Quick Sort:

An iterative version of QuickSort uses a stack to eliminate the need for recursion. It follows the same steps as the recursive version but utilizes a stack data structure.

Algorithm Steps:

• Create an empty stack and push the initial values onto it.
• Perform iterations until the stack is empty.
• Pop values from the stack, partition, and push the indices of the subarrays.

4. Quick Sort on Singly Linked List:

Adapting QuickSort for singly linked lists involves partitioning the list based on a pivot, similar to the array version.

Algorithm Steps:

• Select a pivot from the list.
• Partition the list around the pivot.
• Recursively apply QuickSort to the partitions.

5. Median of Two Sorted Arrays

Finding the median of two sorted arrays involves merging the arrays and finding the middle element.

Algorithm Steps:

• Merge the two sorted arrays.
• If the total length is odd, return the middle element.
• If the total length is even, return the average of the two middle elements.

6. Count Inversions in an Array Using Merge Sort

Counting inversions in an array involves determining the number of pairs of indices (i, j) such that i < j and array[i] > array[j].

Algorithm Steps:

• Apply Merge Sort while counting inversions during the merging step.
• Merge the two halves, counting inversions when elements from the second half are chosen.

7. Closest Pair of Points

The Closest Pair of Points problem involves finding the pair of points with the smallest Euclidean distance among a set of points.

Algorithm Steps:

• Sort the points by their x-coordinates.
• Recursively find the closest pairs in the left and right halves.
• Check for a closer pair that spans the two halves.

8. Strassen’s Matrix Multiplication

Strassen’s Matrix Multiplication is a divide-and-conquer algorithm for multiplying matrices more efficiently than the standard method.

Algorithm Steps:

• Split the input matrices into submatrices.
• Recursively compute seven products.
• Combine the products to form the result.

9. Sort a Nearly Sorted (or K Sorted) Array

Sorting a nearly sorted array involves efficiently sorting an array where each element is at most k positions away from its final sorted position.

Algorithm Steps:

• Create a min-heap of size k + 1.
• Insert the first k + 1 elements into the heap.
• Extract the minimum and insert the next element from the array.

10. Search in an Almost Sorted Array

Searching in an almost sorted array involves finding the position of an element in an array where each element is at most k positions away from its final sorted position.

Algorithm Steps:

• Use a modified binary search to find the element.
• Compare the element with adjacent elements within the range of k.

11. K-th Element of Two Sorted Arrays

Finding the k-th element in two sorted arrays involves comparing the medians of the two arrays and eliminating half of the elements.

Algorithm Steps:

• Compare the medians of the two arrays.
• Eliminate the half that cannot contain the k-th element.
• Repeat the process until the k-th element is found.

12. K’th Smallest/Largest Element in Unsorted Array

Finding the k-th smallest or largest element in an unsorted array involves using QuickSelect, a variation of QuickSort.

Algorithm Steps:

• Choose a pivot and partition the array.
• Recursively apply QuickSelect to the relevant partition.
• Adjust the value of k based on the partitioning.
• Time Complexity of Divide and Conquer Algorithm:

Advantages of Divide and Conquer Algorithm:

• It divides the entire problem into subproblems thus it can be solved parallelly ensuring multiprocessing
• Efficiently uses cache memory without occupying much space.
• Reduces time complexity of the problem.

Disadvantages of Divide and Conquer Algorithm:

• It may crash the system if the recursion is performed rigorously.
• The process of dividing the problem into subproblems and then combining the solutions can require additional time and resources.
• Complexity: Dividing a problem into smaller subproblems can increase the complexity of the overall solution.
• When working with large data sets, the memory requirements for storing the intermediate results of the subproblems can become a limiting factor.

Previously Asked GATE Questions on Divide and Conquer:

Question 1: Which of the following algorithms is NOT a divide & conquer algorithm by nature?

(A) Euclidean algorithm to compute the greatest common divisor
(B) Heap Sort
(C) Cooley-Tukey fast Fourier transform
(D) Quick Sort

Answer: (B)
Explanation: See Divide and Conquer

Question 2: Consider the following C program

C

int main()
{
    int x, y, m, n;
    scanf("%d %d", &x, &y);
    /* x > 0 and y > 0 */
    m = x;
    n = y;
    while (m != n) {
        if (m > n)
            m = m - n;
        else
            n = n - m;
    }
    printf("%d", n);
}

What does the program compute?

(A) x + y using repeated subtraction
(B) x mod y using repeated subtraction
(C) the greatest common divisor of x and y
(D) the least common multiple of x and y

Answer: (C)
Explanation: This is an implementation of Euclid’s algorithm to find GCD

Question 3: Consider the polynomial p(x) = a0 + a1x + a2x^2 +a3x^3, where ai != 0, for all i. The minimum number of multiplications needed to evaluate p on an input x is:

(A) 3
(B) 4
(C) 6
(D) 9

Answer: (A)
Explanation: Multiplications can be minimized using following order for evaluation of the given expression. p(x) = a0 + x(a1 + x(a2 + a3x))

Question 4: Maximum Subarray Sum problem is to find the subarray with maximum sum. For example, given an array {12, -13, -5, 25, -20, 30, 10}, the maximum subarray sum is 45. The naive solution for this problem is to calculate sum of all subarrays starting with every element and return the maximum of all. We can solve this using Divide and Conquer, what will be the worst case time complexity using Divide and Conquer?

(A) O(n)
(B) O(nLogn)
(C) O(Logn)
(D) O(n^2)

Answer: O(B)
Explanation: See http://www.geeksforgeeks.org/divide-and-conquer-maximum-sum-subarray/

Question 5: Consider a situation where you don’t have function to calculate power (pow() function in C) and you need to calculate x^n where x can be any number and n is a positive integer. What can be the best possible time complexity of your power function?

(A) O(n)
(B) O(nLogn)
(C) O(LogLogn)
(D) O(Logn)

Answer: (D)
Explanation: We can calculate power using divide and conquer in O(Logn) time.

Question 6: Consider the problem of searching an element x in an array ‘arr[]’ of size n. The problem can be solved in O(Logn) time if. 1) Array is sorted 2) Array is sorted and rotated by k. k is given to you and k <= n 3) Array is sorted and rotated by k. k is NOT given to you and k <= n 4) Array is not sorted

(A) 1 Only
(B) 1 & 2 only
(C) 1, 2 and 3 only
(D) 1, 2, 3 and 4

Answer: (C)
Explanation: See http://www.geeksforgeeks.org/search-an-element-in-a-sorted-and-pivoted-array/

Question 7: Consider the problem of computing min-max in an unsorted array where min and max are minimum and maximum elements of array. Algorithm A1 can compute min-max in a1 comparisons without divide and conquer. Algorithm A2 can compute min-max in a2 comparisons by scanning the array linearly. What could be the relation between a1 and a2 considering the worst case scenarios?

(A) a1 < a2
(B) a1 > a2
(C) a1 = a2
(D) Depends on the input

Answer: (B)
Explanation: When Divide and Conquer is used to find the minimum-maximum element in an array, Recurrence relation for the number of comparisons is
T(n) = 2T(n/2) + 2 where 2 is for comparing the minimums as well the maximums of the left and right subarrays
On solving, T(n) = 1.5n – 2.
While doing linear scan, it would take 2*(n-1) comparisons in the worst case to find both minimum as well maximum in one pass.

Question 8: Let P be an array containing n integers. Let t be the lowest upper bound on the number of comparisons of the array elements, required to find the minimum and maximum values in an arbitrary array of n elements. Which one of the following choices is correct?

(A) t>2n−2
(B) t>3⌈n/2⌉ and t≤2n−2
(C) t>n and t≤3⌈n/2⌉
(D) t>⌈log2(n)⌉ and t≤n

Answer: (B)
Explanation: It will take t≤2n−2 comparisons without divide and conquer technique. It will take t≤ 3⌈n/2⌉ – 2 with divide and conquer technique.

Question 9: A binary search tree T contains n distinct elements. What is the time complexity of picking an element in T that is smaller than the maximum element in T?

(A) Θ(nlogn)
(B) Θ(n)
(C) Θ(logn)
(D) Θ(1)

Answer: (D)
Explanation: Pick any two elements from the root, and return minimum of these two. So, time is Θ(1).

Question 10: Consider the following array. 

Which algorithm out of the following options uses the least number of comparisons (among the array elements) to sort the above array in ascending order?

(A) Selection sort
(B) Mergesort
(C) Insertion sort
(D) Quicksort using the last element as pivot

Answer: (C)
Explanation: Since, given array is almost sorted in ascending order, so Insertion sort will give its best case with time complexity of order O(n).