Load Balancing on Servers (Randomized Algorithm)
Last Updated :
15 Nov, 2015
Consider a high traffic website that receives millions of requests (of different types) per five minutes, the site has k (for example n = 1000) servers to process the requests. How should the load be balanced among servers?
The solutions that we generally think of are
a) Round Robin
b) Assign new request to a server that has minimum load.
Both of the above approaches look good, but they require additional state information to be maintained for load balancing. Following is a simple approach that works better than above approaches.
Do following whenever a new request comes in,
Pick a random server and assign the request to a random server
The above approach is simpler, lightweight and surprisingly effective. This approach doesn’t calculate existing load on server and doesn’t need time management.
Analysis of above Random Approach
Let us analyze the average load on a server when above approach of randomly picking server is used.
Let there be k request (or jobs) J1, J2, … Jk
Let there be n servers be S1, S2, … Sk.
Let time taken by i’th job be Ti
Let Rij be load on server Si from Job Jj.
Rij is Tj if j’th job (or Jj) is assigned to Si, otherwise 0. Therefore, value of Rij is Tj with probability 1/n and value is 0 with probability (1-1/n)
Let Ri be load on i’th server
Average Load on i'th server 'Ex(Ri)'
[Applying Linearity of Expectation]
=  =
= 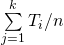 = (Total Load)/n
= (Total Load)/n
So average load on a server is total load divided by n which is a perfect result.
What is the possibility of deviation from average (A particular server gets too much load)?
The average load from above random assignment approach looks good, but there may be possibility that a particular server becomes too loaded (even if the average is ok).
It turns out that the probability of deviation from average is also very low (can be proved using Chernoff bound). Readers can refer below reference links for proves of deviations. For example, in MIT video lecture, it is shown that if there are 2500 requests per unit time and there are 10 servers, then the probability that any particular server gets 10% more load is at most 1/16000. Similar results are shown at the end of second reference also.
So above simple load balancing scheme works perfect. In-fact this scheme is used in load balancers.
References:
http://www.cs.princeton.edu/courses/archive/fall09/cos521/Handouts/probabilityandcomputing.pdf
MIT Video Lecture
Share your thoughts in the comments
Please Login to comment...