Greedy Algorithm Notes for GATE Exam [2024]

In the dynamic landscape of algorithmic design, Greedy Algorithms stand out as powerful tools for solving optimization problems. Aspirants preparing for the GATE Exam 2024 are poised to encounter a range of questions that test their understanding of Greedy Algorithms. These notes aim to provide a concise and insightful overview, unraveling the principles and applications of Greedy Algorithms that are likely to be scrutinized in the upcoming GATE examination.

Introduction to Greedy Algorithms:

What is Greedy Algorithm?

Greedy is an algorithmic paradigm that builds up a solution piece by piece, always choosing the next piece that offers the most obvious and immediate benefit. So the problems where choosing locally optimal also leads to global solution are the best fit for Greedy.

Characteristics of Greedy algorithm:

For a problem to be solved using the Greedy approach, it must follow a few major characteristics:

• There is an ordered list of resources(profit, cost, value, etc.) 
• Maximum of all the resources(max profit, max value, etc.) are taken. 
• For example, in the fractional knapsack problem, the maximum value/weight is taken first according to available capacity. 

Examples of Greedy Algorithm :

Some Famous problems that exhibit Optimal substructure property and can be solved using Greedy approach are :

1. Job sequencing Problem
2. Fractional Knapsack Problem
3. Prim’s algorithm to find Minimum Spanning Tree
4. Activity Selection Problem
5. Dijkstra’s shortest path algorithm

Advantages of the Greedy Approach:

• The greedy approach is easy to implement and typically have less time complexity.
• Greedy algorithms can produce efficient solutions in many cases, especially when the problem has a substructure that exhibits the greedy choice property.
• Greedy algorithms are often faster than other optimization algorithms, such as dynamic programming or branch and bound, because they require less computation and memory.
• The greedy approach can be applied to a wide range of problems, including problems in computer science, operations research, economics, and other fields.
• The greedy approach can be used to solve problems in real-time, such as scheduling problems or resource allocation problems, because it does not require the solution to be computed in advance.
• Greedy algorithms can be used in conjunction with other optimization algorithms, such as local search or simulated annealing, to improve the quality of the solution.

Disadvantages of the Greedy Approach:

• The local optimal solution may not always be globally optimal.
• Greedy algorithms do not always guarantee to find the optimal solution, and may produce suboptimal solutions in some cases.
• The greedy approach relies heavily on the problem structure and the choice of criteria used to make the local optimal choice. If the criteria are not chosen carefully, the solution produced may be far from optimal.
• Greedy algorithms may require a lot of pre-processing to transform the problem into a form that can be solved by the greedy approach.
• Greedy algorithms may not be applicable to problems where the optimal solution depends on the order in which the inputs are processed.

Some of the Important Greedy Algorithms are given below:

Activity Selection Problem:

The activity selection​ problem is an optimization problem used to find the maximum number of activities a person can perform if they can only work on one activity at a time.

Problem Statement: You are given n activities with their start and finish times. Select the maximum number of activities that can be performed by a single person, assuming that a person can only work on a single activity at a time. 

Approach:

The greedy choice is to always pick the next activity whose finish time is the least among the remaining activities and the start time is more than or equal to the finish time of the previously selected activity. We can sort the activities according to their finishing time so that we always consider the next activity as the minimum finishing time activity.

Here in this image we can see the selected activities.

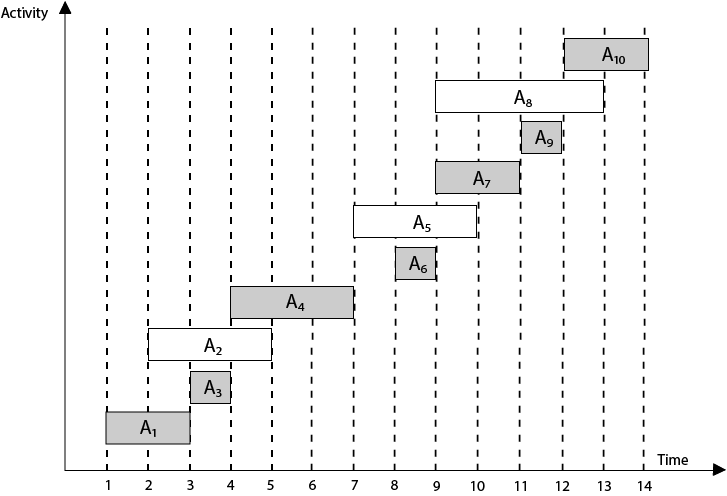
Activity Selection Problem

Time Complexity: O(N * logN)
Auxiliary Space: O(1)

Job Sequencing Problem

The job sequencing problem states that We have a single processor operating system and a set of jobs that have to be completed with given deadline constraints. Our objective is to maximize the profit, given the condition that only one job can be completed at a given time.

Problem Statement : Given an array of jobs where every job has a deadline and associated profit if the job is finished before the deadline. It is also given that every job takes a single unit of time, so the minimum possible deadline for any job is 1. Task is to Maximize the total profit if only one job can be scheduled at a time.

Example:

Input:  Five Jobs with following deadlines and profits

JobID Deadline Profit

  a            2          100
  b            1          19
  c            2          27
 d            1          25
 e            3          15

Output: Following is maximum profit sequence of jobs: c, a, e

Approach: We can solve this problem using greedy approach .

We have to Greedily choose the jobs with maximum profit first, by sorting the jobs in decreasing order of their profit. This would help to maximize the total profit as choosing the job with maximum profit for every time slot will eventually maximize the total profit

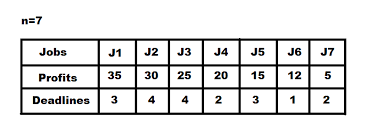
Job Sequencing Problem

Huffman Coding

Huffman coding is a lossless data compression algorithm. The idea is to assign variable-length codes to input characters and lengths of the assigned codes are based on the frequencies of corresponding characters. 

The variable-length codes assigned to input characters are Prefix Codes, means the codes (bit sequences) are assigned in such a way that the code assigned to one character is not the prefix of code assigned to any other character. This is how Huffman Coding makes sure that there is no ambiguity when decoding the generated bitstream.

Let us understand prefix codes with a counter example. Let there be four characters a, b, c and d, and their corresponding variable length codes be 00, 01, 0 and 1. This coding leads to ambiguity because code assigned to c is the prefix of codes assigned to a and b. If the compressed bit stream is 0001, the de-compressed output may be “cccd” or “ccb” or “acd” or “ab”. 

There are mainly two major parts in Huffman Coding:

1. Build a Huffman Tree from input characters.
2. Traverse the Huffman Tree and assign codes to characters.

Steps to build Huffman Tree:

Input is an array of unique characters along with their frequency of occurrences and output is Huffman Tree. 

1. Create a leaf node for each unique character and build a min heap of all leaf nodes (Min Heap is used as a priority queue. The value of frequency field is used to compare two nodes in min heap. Initially, the least frequent character is at root)
2. Extract two nodes with the minimum frequency from the min heap.
   
3. Create a new internal node with a frequency equal to the sum of the two nodes frequencies. Make the first extracted node as its left child and the other extracted node as its right child. Add this node to the min heap.
4. Repeat steps#2 and #3 until the heap contains only one node. The remaining node is the root node and the tree is complete.
   Let us understand the algorithm with an example:

character   Frequency
    a            5
    b           9
    c           12
    d           13
    e           16
    f           45

After Creating Huffman Tree for these characters, our tree will look like below:

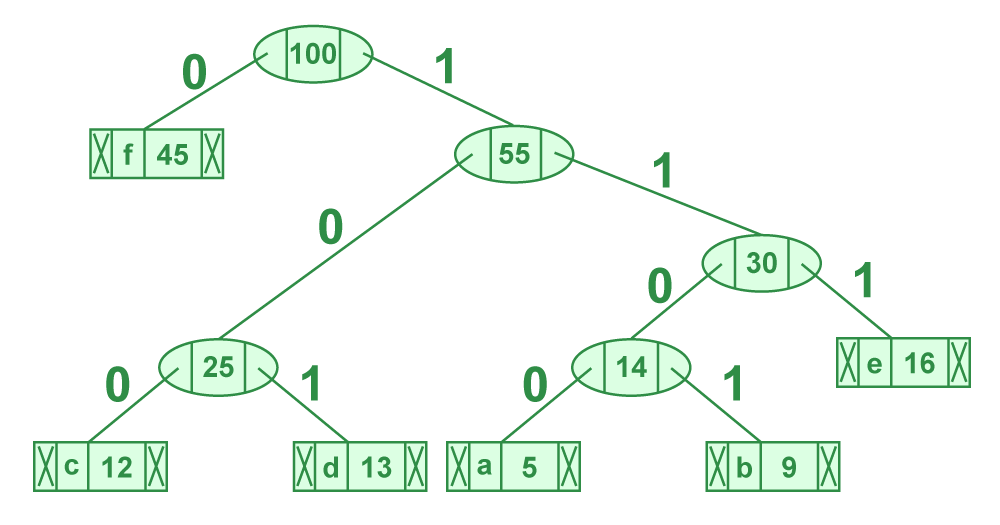
Huffman Tree

Huffman codes for below characters will look like this:

character     code-word
    f                        0
    c                       100
    d                       101
    a                       1100
    b                       1101
    e                        111

Application of Huffman Coding:

Below are some of the applications of Huffman coding in the real life

• Lossless Image Compression
• Using Structures in Images
• Text Compression
• Audio Compression

Fractional Knapsack Problem

We are given a set of items, each with a weight and a value, and we want to find the most valuable subset of items that we can fit into a knapsack with capacity W. The catch is that we can take fractional amounts of each item, so an item can be present in fractional form.

Problem Statement: Given the weights and profits of N items, in the form of {profit, weight} put these items in a knapsack of capacity W to get the maximum total profit in the knapsack. We are allowed to take fractional values in the knapsack.

Example:

Input: arr[] = {{60, 10}, {100, 20}, {120, 30}}, W = 50
Output: 240 
Explanation: By taking items of weight 10 and 20 kg and 2/3 fraction of 30 kg. 
Hence total price will be 60+100+(2/3)(120) = 240

Approach: An efficient solution is to use the Greedy approach. 

The basic idea of the greedy approach is to calculate the ratio profit/weight for each item and sort the item on the basis of this ratio. Then take the item with the highest ratio and add them as much as we can (can be the whole element or a fraction of it).

This will always give the maximum profit because, in each step it adds an element such that this is the maximum possible profit for that much weight.

Time Complexity: O(N * logN)
Auxiliary Space: O(N)

Optimal File Merge Patterns

Optimal merge pattern is a pattern that relates to the merging of two or more sorted files in a single sorted file. here, we have two sorted files containing n and m records respectively then they could be merged together, to obtain one sorted file in time O(n+m).

Problem Statement: Given n number of sorted files, the task is to find the minimum computations done to reach the Optimal Merge Pattern. 
When two or more sorted files are to be merged altogether to form a single file, the minimum computations are done to reach this file are known as Optimal Merge Pattern.

If more than 2 files need to be merged then it can be done in pairs. For example, if need to merge 4 files A, B, C, D. First Merge A with B to get X1, merge X1 with C to get X2, merge X2 with D to get X3 as the output file.

If we have two files of sizes m and n, the total computation time will be m+n. Here, we use the greedy strategy by merging the two smallest size files among all the files present.

Example:

Input: n = 6, size = {2, 3, 4, 5, 6, 7} 
Output: 68 
Explanation: Optimal way to combine these files 

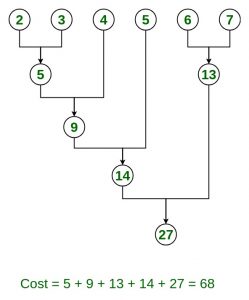
Approach:

Node represents a file with a given size also given nodes are greater than 2 

1. Add all the nodes in a priority queue (Min Heap).{pq.poll = file size}
2. Initialize count = 0 // variable to store file computations.
3. Repeat while (size of priority Queue is greater than 1) 
   1. int weight = pq.poll(); pq.pop;//pq denotes priority queue, remove 1st smallest and pop(remove) it out
   2. weight+=pq.poll()  && pq.pop(); // add the second element and then pop(remove) it out
   3. count +=weight;
   4. pq.add(weight) // add this combined cost to priority queue;  
4. count is the final answer

Time Complexity: O(nlogn)
Auxiliary Space: O(n)

Prim’s Algorithm for Minimum Spanning Tree (MST)

It is a greedy algorithm that is used to find the MST from a graph. Prim’s algorithm finds the subset of edges that includes every vertex of the graph such that the sum of the weights of the edges is minimized.

Prim’s algorithm starts with the single node and explores all the adjacent nodes with all the connecting edges at each step. The edges with the minimal weights causing no cycles in the graph got selected.

How does Prim’s Algorithm Work? 

The working of Prim’s algorithm can be described by using the following steps:

Step 1: Determine an arbitrary vertex as the starting vertex of the MST.
Step 2: Follow steps 3 to 5 till there are vertices that are not included in the MST (known as fringe vertex).
Step 3: Find edges connecting any tree vertex with the fringe vertices.
Step 4: Find the minimum among these edges.
Step 5: Add the chosen edge to the MST if it does not form any cycle.
Step 6: Return the MST and exit

Time Complexity: O(V²), If the input graph is represented using an adjacency list, then the time complexity of Prim’s algorithm can be reduced to O(E * logV) with the help of a binary heap.  In this implementation, we are always considering the spanning tree to start from the root of the graph
Auxiliary Space: O(V)

Kruskal’s Minimum Spanning Tree Algorithm

Kruskal’s algorithm is a well-known algorithm for finding the minimum spanning tree of a graph. It is a greedy algorithm that makes use of the fact that the edges of a minimum spanning tree must form a subset of the edges of any other spanning tree.

In Kruskal’s algorithm, sort all edges of the given graph in increasing order. Then it keeps on adding new edges and nodes in the MST if the newly added edge does not form a cycle. It picks the minimum weighted edge at first and the maximum weighted edge at last. Thus we can say that it makes a locally optimal choice in each step in order to find the optimal solution. Hence this is a Greedy Algorithm.

How to find MST using Kruskal’s algorithm?

Below are the steps for finding MST using Kruskal’s algorithm:

1. Sort all the edges in non-decreasing order of their weight. 
2. Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If the cycle is not formed, include this edge. Else, discard it. 
3. Repeat step#2 until there are (V-1) edges in the spanning tree.

Note: In Step 2 we can use Union Find to detect cycles.

Time Complexity: O(E * logE) or O(E * logV) 
Auxiliary Space: O(V + E), where V is the number of vertices and E is the number of edges in the graph.

Dijkstra’s shortest path algorithm

Dijkstra’s algorithm is a popular algorithms for solving many single-source shortest path problems having non-negative edge weight in the graphs i.e., it is to find the shortest distance between two vertices on a graph. It was conceived by Dutch computer scientist Edsger W. Dijkstra in 1956.

The algorithm maintains a set of visited vertices and a set of unvisited vertices. It starts at the source vertex and iteratively selects the unvisited vertex with the smallest tentative distance from the source. It then visits the neighbours of this vertex and updates their tentative distances if a shorter path is found. This process continues until the destination vertex is reached, or all reachable vertices have been visited.

Need for Dijkstra’s Algorithm (Purpose and Use-Cases):

• The need for Dijkstra’s algorithm arises in many applications where finding the shortest path between two points is crucial.

For example, It can be used in the routing protocols for computer networks and also used by map systems to find the shortest path between starting point and the Destination (as explained in How does Google Maps work?)

Can Dijkstra’s Algorithm work on both Directed and Undirected graphs? 

Yes, Dijkstra’s algorithm can work on both directed graphs and undirected graphs as this algorithm is designed to work on any type of graph as long as it meets the requirements of having non-negative edge weights and being connected.

• In a directed graph, each edge has a direction, indicating the direction of travel between the vertices connected by the edge. In this case, the algorithm follows the direction of the edges when searching for the shortest path.
• In an undirected graph, the edges have no direction, and the algorithm can traverse both forward and backward along the edges when searching for the shortest path.

Algorithm for Dijkstra’s Algorithm:

1. Mark the source node with a current distance of 0 and the rest with infinity.
2. Set the non-visited node with the smallest current distance as the current node.
3. For each neighbour, N of the current node adds the current distance of the adjacent node with the weight of the edge connecting 0->1. If it is smaller than the current distance of Node, set it as the new current distance of N.
4. Mark the current node 1 as visited.
5. Go to step 2 if there are any nodes are unvisited.

Previously Asked GATE Questions for Greedy Algorithm

Question 1: Suppose the letters a, b, c, d, e, f have probabilities 1/2, 1/4, 1/8, 1/16, 1/32, 1/32 respectively. Which of the following is the Huffman code for the letter a, b, c, d, e, f? GATE-2007

(A) 0, 10, 110, 1110, 11110, 11111
(B) 11, 10, 011, 010, 001, 000
(C) 11, 1, 01, 001, 0001, 0000
(D) 110, 100, 010, 000, 001, 111

Correct Answer: (A)
Explanation: We get the following Huffman Tree after applying Huffman Coding Algorithm. The idea is to keep the least probable characters as low as possible by picking them first.

The letters a, b, c, d, e, f have probabilities 
1/2, 1/4, 1/8, 1/16, 1/32, 1/32 respectively. 

                 1
               /   \
              /     \
             1/2    a(1/2)
            /  \
           /    \
          1/4  b(1/4) 
         /   \
        /     \
       1/8   c(1/8) 
      /  \
     /    \
   1/16  d(1/16)
  /  \
 e    f

Question 2: Suppose the letters a, b, c, d, e, f have probabilities 1/2, 1/4, 1/8, 1/16, 1/32, 1/32 respectively. What is the average length of Huffman codes?

(A) 3
(B) 2.1875
(C) 2.25
(D) 1.9375

Correct Answer: (D)
Explanation: We get the following Huffman Tree after applying Huffman Coding Algorithm. The idea is to keep the least probable characters as low as possible by picking them first.

The letters a, b, c, d, e, f have probabilities 
1/2, 1/4, 1/8, 1/16, 1/32, 1/32 respectively. 

                 1
               /   \
              /     \
             1/2    a(1/2)
            /  \
           /    \
          1/4  b(1/4) 
         /   \
        /     \
       1/8   c(1/8) 
      /  \
     /    \
   1/16  d(1/16)
  /  \
 e    f
The average length = (1*1/2 + 2*1/4 + 3*1/8 + 4*1/16 + 5*1/32 + 5*1/32)
                   = 1.9375 

Question 3: Consider the undirected graph below: 

 Using Prim’s algorithm to construct a minimum spanning tree starting with node A, which one of the following sequences of edges represents a possible order in which the edges would be added to construct the minimum spanning tree?

(A) (E, G), (C, F), (F, G), (A, D), (A, B), (A, C)
(B) (A, D), (A, B), (A, C), (C, F), (G, E), (F, G)
(C) (A, B), (A, D), (D, F), (F, G), (G, E), (F, C)
(D) (A, D), (A, B), (D, F), (F, C), (F, G), (G, E)

Correct Answer: (D)
Explanation:
A. False 
The idea behind Prim’s algorithm is to construct a spanning tree – means all vertices must be connected but here vertices are disconnected

B. False 
The idea behind Prim’s algorithm is to construct a spanning tree – means all vertices must be connected but here vertices are disconnected

C. False. 
Prim’s is a greedy algorithm and At every step, it considers all the edges that connect the two sets, and picks the minimum weight edge from these edges. In this option, since weight of AD<AB, so AD must be picked up first (which is not true as per the options).

D.TRUE.

Therefore, Answer is D

Question 4: Consider the weights and values of items listed below. Note that there is only one unit of each item.

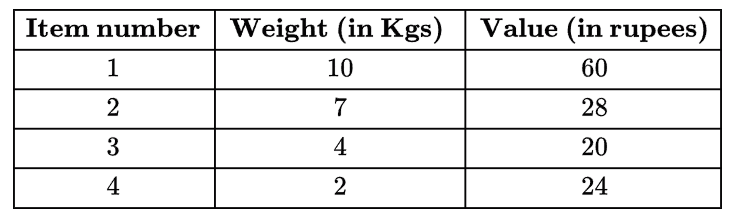
The task is to pick a subset of these items such that their total weight is no more than 11 Kgs and their total value is maximized. Moreover, no item may be split. The total value of items picked by an optimal algorithm is denoted by V_opt. A greedy algorithm sorts the items by their value-to-weight ratios in descending order and packs them greedily, starting from the first item in the ordered list. The total value of items picked by the greedy algorithm is denoted by V_greedy. The value of V_opt − V_greedy is ______ .

(A) 16
(B) 8
(C) 44
(D) 60

Correct Answer: (A)
Explanation: First we will pick item_4 (Value weight ratio is highest). Second highest is item_1, but cannot be picked because of its weight. Now item_3 shall be picked. item_2 cannot be included because of its weight. Therefore, overall profit by V_greedy = 20+24 = 44 Hence, V_opt – V_greedy = 60-44 = 16 So, answer is 16.

Question 5: A text is made up of the characters a, b, c, d, e each occurring with the probability 0.11, 0.40, 0.16, 0.09 and 0.24 respectively. The optimal Huffman coding technique will have the average length of:

(A) 2.40
(B) 2.16
(C) 2.26
(D) 2.15

Correct Answer: (B)
Explanation: a = 0.11 b = 0.40 c = 0.16 d = 0.09 e = 0.24 we will draw a huffman tree.
now huffman coding for character:

 a = 1111
      b = 0
      c = 110
      d = 1111
      e = 10
length for each character = no of bits * frequency of occurrence:
a = 4 * 0.11
  = 0.44
b = 1 * 0.4
  =  0.4
c = 3 * 0.16
  = 0.48
d = 4 * 0.09
  =  0.36 
e = 2 * 0.24
  = 0.48
Now add these lenght for average length:
 0.44 + 0.4 + 0.48 + 0.36 + 0.48 = 2.16

Question 6: Which of the following is true about Huffman Coding.

(A) Huffman coding may become lossy in some cases
(B) Huffman Codes may not be optimal lossless codes in some cases
(C) In Huffman coding, no code is prefix of any other code.
(D) All of the above

Correct Answer: (C)
Explanation: Huffman coding is a lossless data compression algorithm. The codes assigned to input characters are Prefix Codes, means the codes are assigned in such a way that the code assigned to one character is not prefix of code assigned to any other character. This is how Huffman Coding makes sure that there is no ambiguity when decoding.

Question 7: Consider a complete undirected graph with vertex set {0, 1, 2, 3, 4}. Entry W(ij) in the matrix W below is the weight of the edge {i, j}. What is the minimum possible weight of a spanning tree T in this graph such that vertex 0 is a leaf node in the tree T?

(A) 7
(B) 8
(C) 9
(D) 10

Correct Answer: (D)

Question 8: Kruskal’s algorithm for finding a minimum spanning tree of a weighted graph G with n vertices and m edges has the time complexity of:

(A) O(n²)
(B) O(mn)
(C) O(m²)
(D) O(m log n)

Correct Answer: (D)

Question 9: In an unweighted, undirected connected graph, the shortest path from a node S to every other node is computed most efficiently, in terms of time complexity by

(A) Dijkstra’s algorithm starting from S
(B) Warshall’s algorithm
(C) Performing a DFS starting from S
(D) Performing a BFS starting from S

Correct Answer: (D)

Question 10: Let G = (V, E) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighted edge (u, v) ∈ V × V is added to G. The worst case time complexity of determining if T is still an MST of the resultant graph is

(A) Θ( |E|+|V| )
(B) Θ( |E|*|V| )
(C) Θ( |E| log(|V|) )
(D) Θ( |V| )

Correct Answer: (D)