Data Structures and Algorithms | Set 29
Last Updated :
13 Dec, 2022
Following questions have been asked in GATE 2012 exam.
1) The recurrence relation capturing the optimal time of the Tower of Hanoi problem with n discs is
(A) T(n) = 2T(n – 2) + 2
(B) T(n) = 2T(n – 1) + n
(C) T(n) = 2T(n/2) + 1
(D) T(n) = 2T(n – 1) + 1
Answer (D)
Following are the steps to follow to solve Tower of Hanoi problem recursively.
Let the three pegs be A, B and C. The goal is to move n pegs from A to C.
To move n discs from peg A to peg C:
move n-1 discs from A to B. This leaves disc n alone on peg A
move disc n from A to C
move n?1 discs from B to C so they sit on disc n
The recurrence function T(n) for time complexity of the above recursive solution can be written as following.
T(n) = 2T(n-1) + 1
2) Consider the directed graph shown in the figure below. There are multiple shortest paths between vertices S and T. Which one will be reported by Dijkstra?s shortest path algorithm? Assume that, in any iteration, the shortest path to a vertex v is updated only when a strictly shorter path to v is discovered.
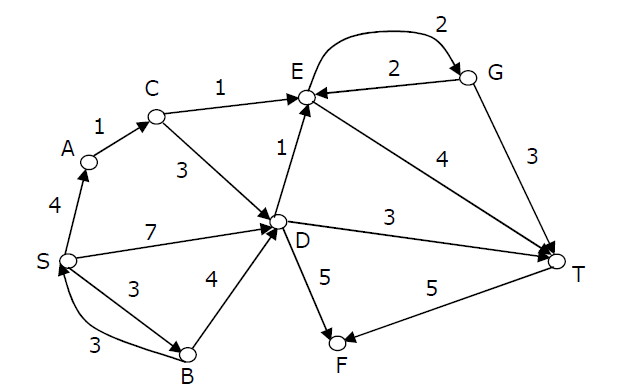
(A) SDT
(B) SBDT
(C) SACDT
(D) SACET
Answer (D)
3) Suppose a circular queue of capacity (n – 1) elements is implemented with an array of n elements. Assume that the insertion and deletion operation are carried out using REAR and FRONT as array index variables, respectively. Initially, REAR = FRONT = 0. The conditions to detect queue full and queue empty are
(A) Full: (REAR+1) mod n == FRONT, empty: REAR == FRONT
(B) Full: (REAR+1) mod n == FRONT, empty: (FRONT+1) mod n == REAR
(C) Full: REAR == FRONT, empty: (REAR+1) mod n == FRONT
(D) Full: (FRONT+1) mod n == REAR, empty: REAR == FRONT
Answer (A)
See this for details.
Please see GATE Corner for all previous year paper/solutions/explanations, syllabus, important dates, notes, etc.
Please write comments if you find any of the answers/explanations incorrect, or you want to share more information about the topics discussed above.
Share your thoughts in the comments
Please Login to comment...