Graph Data Structure Notes for GATE Exam [2024]

Graphs, a fundamental concept in computer science and mathematics, serve as powerful tools for modeling and solving a myriad of real-world problems. As aspirants gear up for the GATE Exam 2024, a comprehensive understanding of graph data structures becomes paramount. These notes aim to provide a concise and illuminating guide to graph data structures, unraveling the principles, representations, and algorithms associated with them, all of which are essential for mastering this topic in the GATE examination.

What is Graph?

A Graph is a non-linear data structure consisting of vertices and edges. The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph is composed of a set of vertices( V ) and a set of edges( E ). The graph is denoted by G(V, E).

Components of a Graph

• Vertices: Vertices are the fundamental units of the graph. Sometimes, vertices are also known as vertex or nodes. Every node/vertex can be labeled or unlabelled.
• Edges: Edges are drawn or used to connect two nodes of the graph. It can be ordered pair of nodes in a directed graph. Edges can connect any two nodes in any possible way. There are no rules. Sometimes, edges are also known as arcs. Every edge can be labelled/unlabelled.

Breadth First Search or BFS in Graph

The Breadth First Search (BFS) algorithm is used to search a graph data structure for a node that meets a set of criteria. It starts at the root of the graph and visits all nodes at the current depth level before moving on to the nodes at the next depth level.

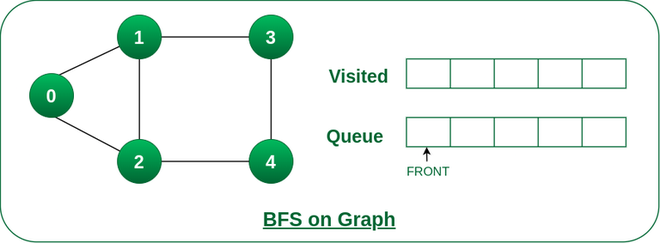
BFS

Time Complexity: O(V+E), where V is the number of nodes and E is the number of edges.
Auxiliary Space: O(V)

Depth First Search or DFS in Graph

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.

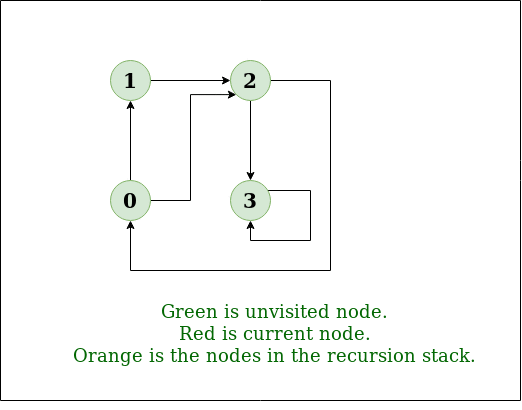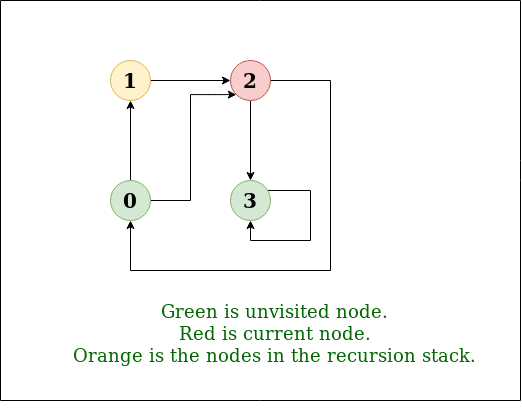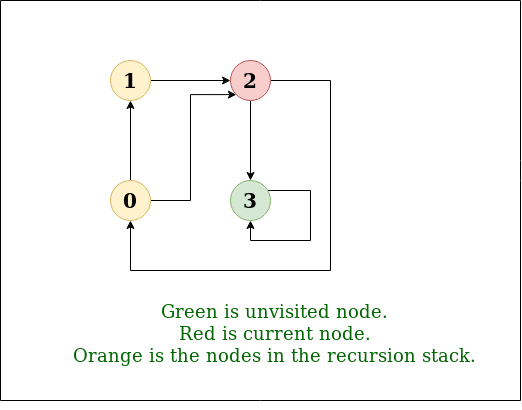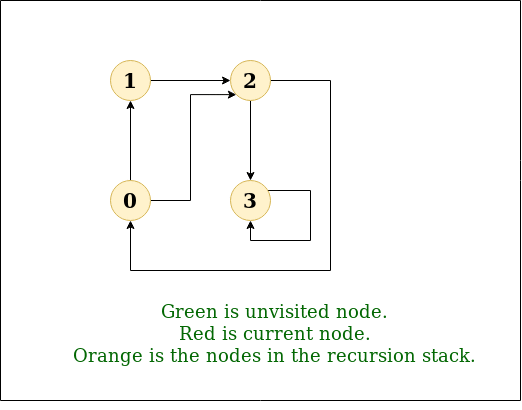
DFS

Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Auxiliary Space: O(V + E), since an extra visited array of size V is required, And stack size for iterative call to DFS function.

Types of Graphs

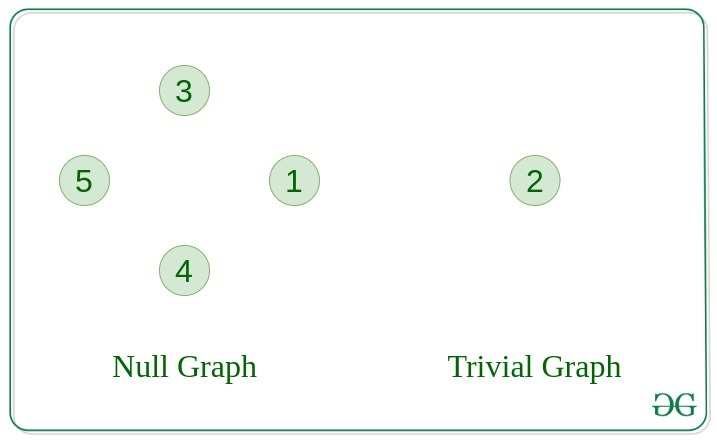
1. Null Graph

A graph is known as a null graph if there are no edges in the graph.

2. Trivial Graph

Graph having only a single vertex, it is also the smallest graph possible.

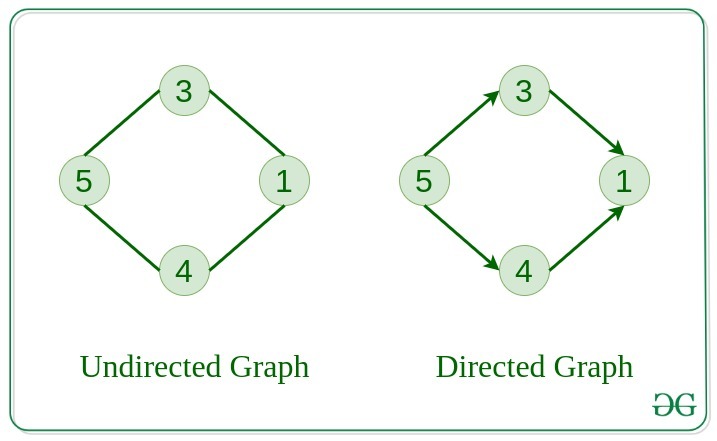
3. Undirected Graph

A graph in which edges do not have any direction. That is the nodes are unordered pairs in the definition of every edge. 

4. Directed Graph

A graph in which edge has direction. That is the nodes are ordered pairs in the definition of every edge.

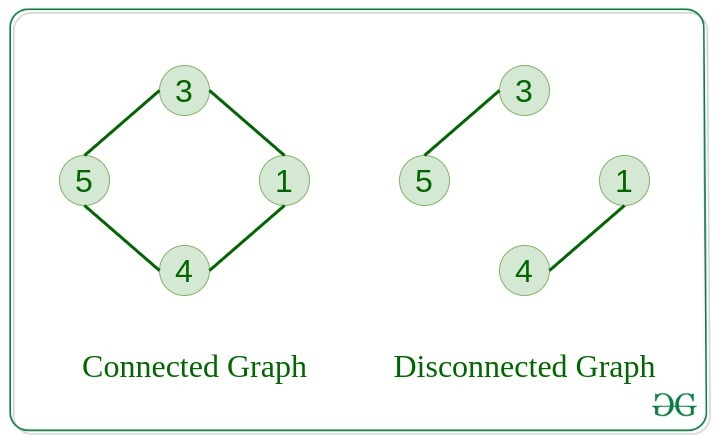
5. Connected Graph

The graph in which from one node we can visit any other node in the graph is known as a connected graph. 

6. Disconnected Graph

The graph in which at least one node is not reachable from a node is known as a disconnected graph.

7. Regular Graph

The graph in which the degree of every vertex is equal to K is called K regular graph.

8. Complete Graph

The graph in which from each node there is an edge to each other node.

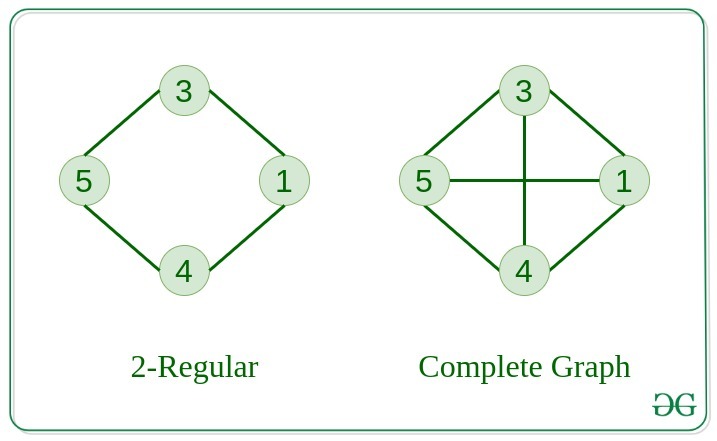
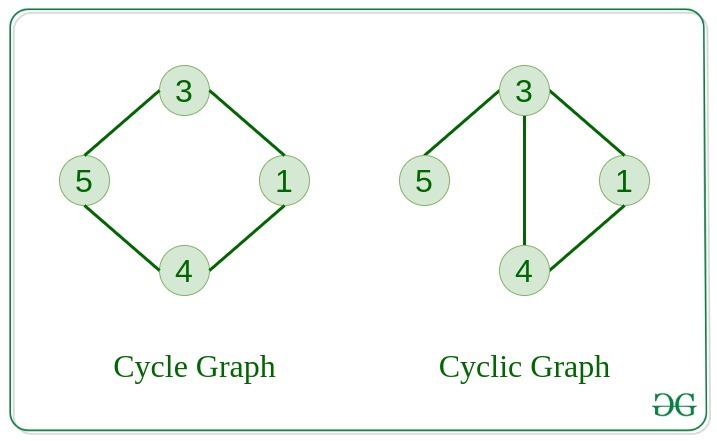
9. Cycle Graph

The graph in which the graph is a cycle in itself, the degree of each vertex is 2. 

10. Cyclic Graph

A graph containing at least one cycle is known as a Cyclic graph.

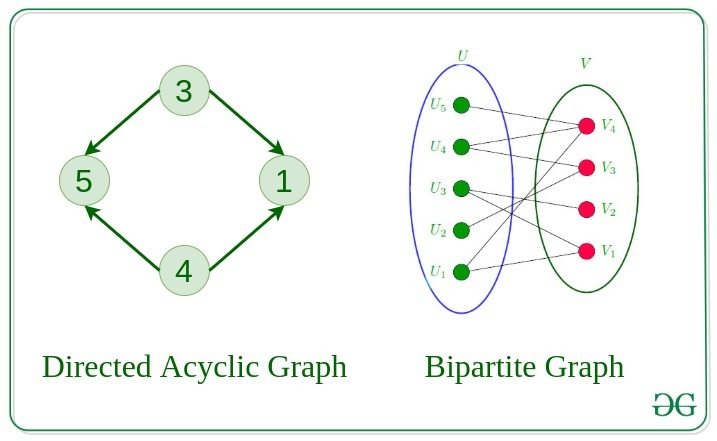
11. Directed Acyclic Graph

A Directed Graph that does not contain any cycle. 

12. Bipartite Graph

A graph in which vertex can be divided into two sets such that vertex in each set does not contain any edge between them.

 13. Weighted Graph

• A graph in which the edges are already specified with suitable weight is known as a weighted graph. 
•  Weighted graphs can be further classified as directed weighted graphs and undirected weighted graphs. 

Representations of Graph

Here are the two most common ways to represent a graph :

1. Adjacency Matrix
2. Adjacency List

Adjacency Matrix

An adjacency matrix is a way of representing a graph as a matrix of boolean (0’s and 1’s).

Let’s assume there are n vertices in the graph So, create a 2D matrix adjMat[n][n] having dimension n x n.

• If there is an edge from vertex i to j, mark adjMat[i][j] as 1.
• If there is no edge from vertex i to j, mark adjMat[i][j] as 0.

Representation of Directed Graph to Adjacency Matrix:

The below figure shows a directed graph. Initially, the entire Matrix is ​​initialized to 0. If there is an edge from source to destination, we insert 1 for that particular adjMat[destination].

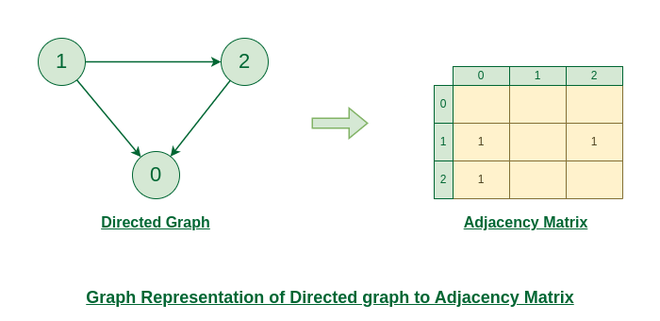
Directed Graph to Adjacency Matrix

Adjacency List

An array of Lists is used to store edges between two vertices. The size of array is equal to the number of vertices (i.e, n). Each index in this array represents a specific vertex in the graph. The entry at the index i of the array contains a linked list containing the vertices that are adjacent to vertex i.

Let’s assume there are n vertices in the graph So, create an array of list of size n as adjList[n].

• adjList[0] will have all the nodes which are connected (neighbour) to vertex 0.
• adjList[1] will have all the nodes which are connected (neighbour) to vertex 1 and so on.

Representation of Directed Graph to Adjacency list:

The below directed graph has 3 vertices. So, an array of list will be created of size 3, where each indices represent the vertices. Now, vertex 0 has no neighbours. For vertex 1, it has two neighbour (i.e, 0 and 2) So, insert vertices 0 and 2 at indices 1 of array. Similarly, for vertex 2, insert its neighbours in array of list.

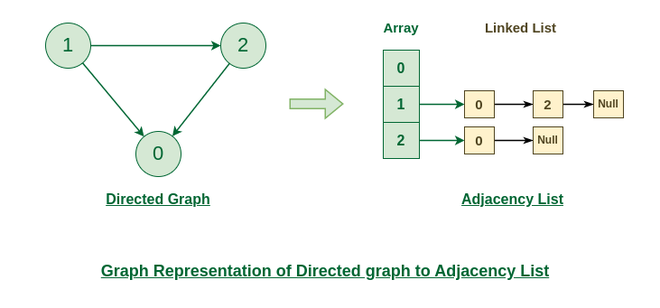
Directed Graph to Adjacency list

Basic Properties of a Graph

A Graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph.

The basic properties of a graph include:

1. Vertices (nodes): The points where edges meet in a graph are known as vertices or nodes. A vertex can represent a physical object, concept, or abstract entity.
2. Edges: The connections between vertices are known as edges. They can be undirected (bidirectional) or directed (unidirectional).
3. Weight: A weight can be assigned to an edge, representing the cost or distance between two vertices. A weighted graph is a graph where the edges have weights.
4. Degree: The degree of a vertex is the number of edges that connect to it. In a directed graph, the in-degree of a vertex is the number of edges that point to it, and the out-degree is the number of edges that start from it.
5. Path: A path is a sequence of vertices that are connected by edges. A simple path does not contain any repeated vertices or edges.
6. Cycle: A cycle is a path that starts and ends at the same vertex. A simple cycle does not contain any repeated vertices or edges.
7. Connectedness: A graph is said to be connected if there is a path between any two vertices. A disconnected graph is a graph that is not connected.
8. Planarity: A graph is said to be planar if it can be drawn on a plane without any edges crossing each other.
9. Bipartiteness: A graph is said to be bipartite if its vertices can be divided into two disjoint sets such that no two vertices in the same set are connected by an edge.

Applications of Graph Data Structure

• In Computer science graphs are used to represent the flow of computation.
• Google maps uses graphs for building transportation systems, where intersection of two(or more) roads are considered to be a vertex and the road connecting two vertices is considered to be an edge, thus their navigation system is based on the algorithm to calculate the shortest path between two vertices.
• In Facebook, users are considered to be the vertices and if they are friends then there is an edge running between them. Facebook’s Friend suggestion algorithm uses graph theory. Facebook is an example of undirected graph.
• In World Wide Web, web pages are considered to be the vertices. There is an edge from a page u to other page v if there is a link of page v on page u. This is an example of Directed graph. It was the basic idea behind Google Page Ranking Algorithm.
• In Operating System, we come across the Resource Allocation Graph where each process and resources are considered to be vertices. Edges are drawn from resources to the allocated process, or from requesting process to the requested resource. If this leads to any formation of a cycle then a deadlock will occur.
• In mapping system we use graph. It is useful to find out which is an excellent place from the location as well as your nearby location. In GPS we also use graphs.
• Facebook uses graphs. Using graphs suggests mutual friends. it shows a list of the f following pages, friends, and contact list.
• Microsoft Excel uses DAG means Directed Acyclic Graphs.
• In the Dijkstra algorithm, we use a graph. we find the smallest path between two or many nodes.

Advantages of Graph:

• Representing complex data: Graphs are effective tools for representing complex data, especially when the relationships between the data points are not straightforward. They can help to uncover patterns, trends, and insights that may be difficult to see using other methods.
• Efficient data processing: Graphs can be processed efficiently using graph algorithms, which are specifically designed to work with graph data structures. This makes it possible to perform complex operations on large datasets quickly and effectively.
• Network analysis: Graphs are commonly used in network analysis to study relationships between individuals or organizations, as well as to identify important nodes and edges in a network. This is useful in a variety of fields, including social sciences, business, and marketing.
• Pathfinding: Graphs can be used to find the shortest path between two points, which is a common problem in computer science, logistics, and transportation planning.
• Visualization: Graphs are highly visual, making it easy to communicate complex data and relationships in a clear and concise way. This makes them useful for presentations, reports, and data analysis.
• Machine learning: Graphs can be used in machine learning to model complex relationships between variables, such as in recommendation systems or fraud detection.

Disadvantages of Graph

• Limited representation: Graphs can only represent relationships between objects, and not their properties or attributes. This means that in order to fully understand the data, it may be necessary to supplement the graph with additional information.
• Difficulty in interpretation: Graphs can be difficult to interpret, especially if they are large or complex. This can make it challenging to extract meaningful insights from the data, and may require advanced analytical techniques or domain expertise.
• Scalability issues: As the number of nodes and edges in a graph increases, the processing time and memory required to analyze it also increases. This can make it difficult to work with large or complex graphs.
• Data quality issues: Graphs are only as good as the data they are based on, and if the data is incomplete, inconsistent, or inaccurate, the graph may not accurately reflect the relationships between objects.
• Lack of standardization: There are many different types of graphs, and each has its own strengths and weaknesses. This can make it difficult to compare graphs from different sources, or to choose the best type of graph for a given analysis.
• Privacy concerns: Graphs can reveal sensitive information about individuals or organizations, which can raise privacy concerns, especially in social network analysis or marketing.

Gate Previous Year Problems on Graph Data Structure

1. Consider the tree arcs of a BFS traversal from a source node W in an unweighted, connected, undirected graph. The tree T formed by the tree arcs is a data structure for computing. [GATE CSE 2014 Set 2]

(A) the shortest path between every pair of vertices.

(B) the shortest path from W to every vertex in the graph.

(C) the shortest paths from W to only those nodes that are leaves of T.

(D) the longest path in the graph.

Solution: Correct answer is (B)

2. Traversal of a graph is somewhat different from the tree because [GATE CSE 2006 Set 1]

(A) There can be a loop in a graph, so we must maintain a visited flag for every vertex

(B) DFS of a graph uses the stack, but the inorder traversal of a tree is recursive

(C) BFS of a graph uses a queue, but a time-efficient BFS of a tree is recursive.

(D) All of the above

Solution: Correct answer is (A)

Explanation: There can be a loop in a graph, and due to this, we must maintain a visited flag for every vertex.

3. What are the suitable Data Structures for the following algorithms? [GATE CSE 2013 Set 2]

1) Breadth-First Search                           

2) Depth First Search                            

3) Prim’s Minimum Spanning Tree                 

4) Kruskal’s Minimum Spanning Tree               

(A)

1) Stack

2) Queue

3) Priority Queue

4) Union Find

(B)

1) Queue

2) Stack

3) Priority Queue

4) Union Find

(C)

1) Stack

2) Queue

3) Union Find

4) Priority Queue 

(D)

1) Priority Queue

2) Queue

3) Stack

4) Union Find

Solution: (B)

Explanation: 1) Queue is used in  Breadth-First Search

2) Stack is used in  depth-first search-dfs

3) Priority Queue is used in Prim’s Minimum Spanning Tree.

4) Union Find is used in Kruskal’s Minimum Spanning Tree. 

4. Let G be a weighted graph with edge weights greater than one and G’ be the graph constructed by squaring the weights of edges in G. LetT and T’ be the minimum spanning trees of G and G’ respectively, with total weights t and t’. Which of the following statements is TRUE? [GATE CSE 2020 ]

(A) T’ = T with total weight t’ = t^2

(B) T’ = T with total weight t’ < t^2

(C) T’ =t- T but total weight t’ = t^2

(D) None of these

Solution: (D)

5. The Breadth-First Search algorithm has been implemented with the help of a queue. What is a possible order of visiting the nodes of the following graph is

(A) NQMPOR

(B) QMNPOR

(C) QMNPRO

(D) MNOPQR

.

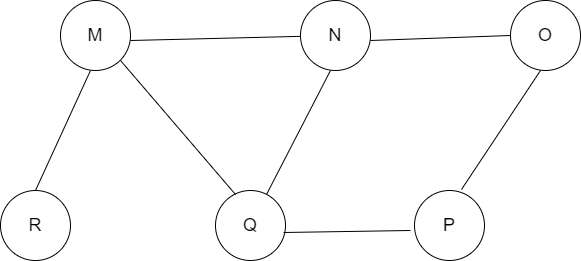
Solution: (C)

Explanation: Option (A) is NQMPOR. It cannot be BFS because P is visited before O here.

Option (D) is MNOPQR. It cannot be a BFS because the traversal begins with M, but O has been visited before N and Q.

In BFS, every adjacent must be called before adjacent of adjacent.

(B) and (C) correspond to QMNP. Before N and P, M had been added to the queue (because M comes before NP in QMNP). R is placed in the line before N and P’s neighbors because it is M’s neighbor (which is O). As a result, R is visited first, followed by O.

6. Let G be an undirected graph. Consider a depth-first traversal of G, where T is the depth-first search tree that results. Let u be the first new (unvisited) vertex visited after u in the traversal, and v be its first new (unvisited) vertex visited after u. Which of the assertions below is always true? [GATE CSE 2014 ]

(A) In G, u,v must be an edge, while in T, u is a descendent of v. 

(B) In G, u,v must be an edge, while in T, v is a descendent of u. 

(C) If u,v in G is not an edge, then u in T is a leaf 

(D) If u,v in G is not an edge, then u and v in T must have the same parent.

Solution: (C)

Explanation:

In  DFS, if ‘v’ is visited

after ‘u,’ one of the following is true.

1) (u, v) is an edge.

u

/ \

v w

/ / \

x y z

2) A leaf node is ‘u.’

w

/ \

x v

/ / \

u y z

In DFS, after we have visited a node, we first go back to all children who were not visited. If no children are left unvisited(u is a leaf), then control goes back to the parent, and the parent then visits the subsequent unvisited children.

7. Which of the two traversals (BFS and DFS) may be used to find if there is a path from s to t given two vertices in a graph s and t? [GATE CSE 2014 Set 2]

(A) Only BFS

(B) Only DFS

(C) Both BFS and DFS

(D) Neither BFS nor DFS

Solution: (C)

Explanation: Both traversals can be used to see if there is a path from s to t.

8. The statement written below is true or false? [GATE CSE 2021]

If a directed graph’s DFS contains a back edge, any other directed graph’s DFS will also have at least a single back edge.

(A) True

(B) False

Solution: (A)

Explanation: A cycle in the graph is called its back edge. So if we get a cycle, all DFS traversals would contain at least one back edge.

9. Which of the condition written below is sufficient to detect a cycle in a directed graph? [GATE CSE 2008]

(A) There is an edge from a currently visited node to an already seen node.

(B) There is an edge from the currently visited node to an ancestor of the currently visited node in the forest of DFS.

(C) Every node is seen two times in DFS.

(D) None of the above

Solution: (B)

Explanation: If there is an edge from the currently visited node to an ancestor of the currently visited node in the forest of DFS, it means a cycle is formed. As this is an apparent condition about cycle formation, so this condition is sufficient.

10. If the finishing time f[u] > f[v] of DFS for two vertices u and v in a graph G which is directed, and u and v are in the DFS tree same as each other in the DFS forest, then u is an ancestor of v in the depth-first tree. [GATE CSE 2014 Set 2]

(A) True

(B) False

Solution: (B)

Explanation: In a graph that contains three nodes, r u and v, with edges (r; u) and (r; v), and r is the starting point for the DFS, u and v are siblings in the DFS tree; neither as the ancestor of the other.

11.  Is the statement written below true or false? [GATE CSE 2015]

A DFS of a directed graph generally produces the exact number of edges of a tree, i.e., not dependent on the order in which vertices are considered for DFS.

(A) True

(B) False

Solution: (B)

Explanation: Consider the following graph. If we start from ‘a’, then there is one tree edge. If we start from ‘b,’ there is no tree edge.

a—->b