As the GATE Exam 2024 is coming up, having a good grasp of dynamic programming is really important for those looking to tackle tricky computational problems. These notes are here to help you understand the basic principles, strategies, and real-life uses of dynamic programming. They’re like a handy guide to becoming a pro at dynamic programming, making it easier for you to ace the GATE exam. So, get ready to dive into the world of dynamic programming and make problem-solving a breeze!
What is Dynamic Programming?
Dynamic Programming is mainly an optimization over plain recursion. Wherever we see a recursive solution that has repeated calls for the same inputs, we can optimize it using dynamic Programming. The idea is to simply store the results of subproblems so that we do not have to re-compute them when needed later. This simple optimization reduces time complexities from exponential to polynomial.
Dynamic Programming is an algorithmic paradigm that solves a given complex problem by breaking it into subproblems using recursion and storing the results of subproblems to avoid computing the same results again.
Following are the two main properties of a problem that suggest that the given problem can be solved using dynamic programming.
- Overlapping Subproblems
- Optimal Substructure
Like Divide and Conquer, Dynamic Programming combines solutions to sub-problems. Dynamic Programming is mainly used when solutions to the same subproblems are needed again and again. In dynamic programming, computed solutions to subproblems are stored in a table so that these don’t have to be recomputed. So dynamic Programming is not useful when there are no common (overlapping) subproblems because there is no point in storing the solutions if they are not needed again. For example, Binary Search doesn’t have common subproblems. If we take the example of following a recursive program for Fibonacci Numbers, there are many subproblems that are solved again and again.
A given problem is said to have Optimal Substructure Property if the optimal solution of the given problem can be obtained by using the optimal solution to its subproblems instead of trying every possible way to solve the subproblems.
Standard problems on Dynamic Programming:
A longest common subsequence (LCS) is defined as the longest subsequence which is common in all given input sequences.
Examples:
Input: S1 = “AGGTAB”, S2 = “GXTXAYB”
Output: 4
Explanation: The longest subsequence which is present in both strings is “GTAB”.
Matrix chain multiplication is an optimization problem that needs the most efficient method of multiplying a given sequence of matrices. The problem is not to perform the multiplications, but rather to determine the order of the matrix multiplications involved. Dynamic programming could be used to solve the problem.
Example:
Input: arr[] = {40, 20, 30, 10, 30}
Output: 26000
Explanation:There are 4 matrices of dimensions 40×20, 20×30, 30×10, 10×30.
Let the input 4 matrices be A, B, C and D.
The minimum number of multiplications are obtained by
putting parenthesis in following way (A(BC))D.
The minimum is 20*30*10 + 40*20*10 + 40*10*30

Matrix Chain Multilpication
The 0/1 knapsack problem represents that either all or none of the items in a knapsack are completely filled. For example, consider two items weighing 2kg and 3kg, respectively. If we select the 2kg item, we cannot select a 1kg item from the 2kg item (item is not divisible); we must select the entire 2kg item. This is a 0/1 knapsack problem in which we either completely pick the item or pick that item. Dynamic programming is used to solve the 0/1 knapsack problem.
Example:
Input: N = 3, W = 4, profit[] = {1, 2, 3}, weight[] = {4, 5, 1}
Output: 3
Explanation: There are two items which have weight less than or equal to 4. If we select the item with weight 4, the possible profit is 1. And if we select the item with weight 1, the possible profit is 3. So the maximum possible profit is 3. Note that we cannot put both the items with weight 4 and 1 together as the capacity of the bag is 4.
Given a cost matrix cost[][] and a position (M, N) in cost[][], write a function that returns cost of minimum cost path to reach (M, N) from (0, 0). Each cell of the matrix represents a cost to traverse through that cell. The total cost of a path to reach (M, N) is the sum of all the costs on that path (including both source and destination). You can only traverse down, right and diagonally lower cells from a given cell, i.e., from a given cell (i, j), cells (i+1, j), (i, j+1), and (i+1, j+1) can be traversed.
Example:
Input:
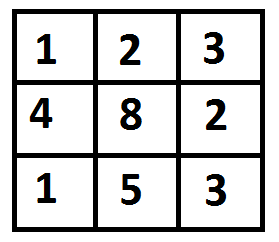
Min Cost Path
The path with minimum cost is highlighted in the following figure. The path is (0, 0) –> (0, 1) –> (1, 2) –> (2, 2). The cost of the path is 8 (1 + 2 + 2 + 3).
Output:
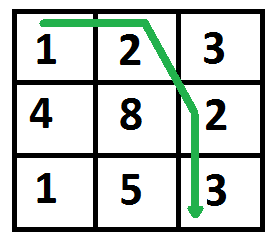
Min Cost Path
The subset sum problem is a decision problem. In its most general form, there is a multiset of integers and a target sum, and the problem is to determine whether any subset of the integers sums exactly. It is well known that the problem is NP-hard. Furthermore, some restricted variants of it are NP-complete as well.
Example:
Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 9
Output: True
Explanation: There is a subset (4, 5) with sum 9.
Bellman-Ford Algorithm is a single source shortest path algorithm that determines the shortest path between a given source vertex and every other vertex in a graph. This algorithm can be used on both weighted and unweighted graphs.
A Bellman-Ford algorithm is also guaranteed to find the shortest path in a graph, similar to Dijkstra’s algorithm. Although Bellman-Ford is slower than Dijkstra’s algorithm, it is capable of handling graphs with negative edge weights, which makes it more versatile. The shortest path cannot be found if there exists a negative cycle in the graph. If we continue to go around the negative cycle an infinite number of times, then the cost of the path will continue to decrease (even though the length of the path is increasing). As a result, Bellman-Ford is also capable of detecting negative cycles, which is an important feature.
The Floyd Warshall Algorithm is an all pair shortest path algorithm unlike Dijkstra and Bellman Ford which are single source shortest path algorithms. This algorithm works for both the directed and undirected weighted graphs. But, it does not work for the graphs with negative cycles (where the sum of the edges in a cycle is negative). It follows Dynamic Programming approach to check every possible path going via every possible node in order to calculate shortest distance between every pair of nodes.
A number is non-decreasing if every digit (except the first one) is greater than or equal to the previous digit. For example, 223, 4455567, 899, are non-decreasing numbers.
So, given the number of digits n, you are required to find the count of total non-decreasing numbers with n digits.
Examples:
Input: n = 1
Output: count = 10
Input: n = 2
Output: count = 55
The problem is to find the smallest power of 2 that is greater than or equal to a positive integer ‘n’. We must devise an algorithm to compute this value efficiently without using the power function. This can be useful in a variety of situations, including determining the appropriate size for data structures and optimizing algorithms.
Example:
Input: n = 5
Output: 8
Input: n = 17
Output: 32
Previously Asked Problems of Dynamic Programming on GATE:
Q1. [GATE-CS-2016]
The Floyd-Warshall algorithm for all-pair shortest paths computation is based on
(A) Greedy Paradigm
(B) Divide-and-Conquer Paradigm
(C) Dynamic Programming Paradigm
(D) Neither Greedy nor Divide-and- Conquer nor Dynamic Programming Paradigm
Ans: (C) Dynamic Programming Paradigm
Q2. [GATE-CS-2015]
List-I
A. Prim’s algorithm for minimum spanning tree
B. Floyd-Warshall algorithm for all pairs shortest paths
C. Mergesort
D. Hamiltonian circuit
List-II
1. Backtracking
2. Greedy method
3. Dynamic programming
4. Divide and conquer
Codes:
A B C D
(a) 3 2 4 1
(b) 1 2 4 3
(c) 2 3 4 1
(d) 2 1 3 4
Options:
(A): a
(B): b
(C): c
(D): d
Ans: (C)
Q3. [GATE-CS-2017]
Kadane algorithm is generally used to find out.
(A) Maximum sum subsequence present in an array
(B) Maximum sum subarray present in an array
(C) Maximum product subsequence present in an array
(D) Maximum product subarray present in an array
Ans: (B) Maximum sum subarray present in an array
Q4. [GATE-CS-2017]
Which of the standard algorithms shown below is not based on Dynamic Programming?
(A) Prim’s Minimum Spanning Tree
(B) Bellman-Ford Algorithm for single-source shortest path
(C) Floyd Warshall Algorithm for all-pairs shortest paths
(D) 0-1 Knapsack problem
Ans: (A) Prim’s Minimum Spanning Tree
Q5. [GATE-CS-2014]
Consider two strings A = \”qpqrr\” and B = \”pqprqrp\”. Let x be the length of the longest common subsequence (not necessarily contiguous) between A and B and let y be the number of such longest common subsequences between A and B. Then x + 10y = ___.
(A) 33
(B) 23
(C) 43
(D) 34
Ans: (D) 34
Share your thoughts in the comments
Please Login to comment...