Stack Notes for GATE Exam [2024]

Stacks, a fundamental data structure in computer science, are crucial for understanding algorithmic paradigms and solving complex computational problems. As candidates gear up for the GATE Exam 2024, a solid grasp of stack concepts is indispensable. These notes are designed to provide a concise yet comprehensive overview of stacks, covering key topics that are likely to be assessed in the GATE examination.

Introduction to Stack:

A stack is a linear data structure in which the insertion of a new element and removal of an existing element takes place at the same end represented as the top of the stack.

To implement the stack, it is required to maintain the pointer to the top of the stack, which is the last element to be inserted because we can access the elements only on the top of the stack.

LIFO (Last In First Out) in Stack:

This strategy states that the element that is inserted last will come out first. You can take a pile of plates kept on top of each other as a real-life example. The plate which we put last is on the top and since we remove the plate that is at the top, we can say that the plate that was put last comes out first.

Basic Operations on Stack

In order to make manipulations in a stack, certain operations are provided to us.

• push() to insert an element into the stack
• pop() to remove an element from the stack
• top() Returns the top element of the stack.
• isEmpty() returns true if the stack is empty else false.
• size() returns the size of the stack.

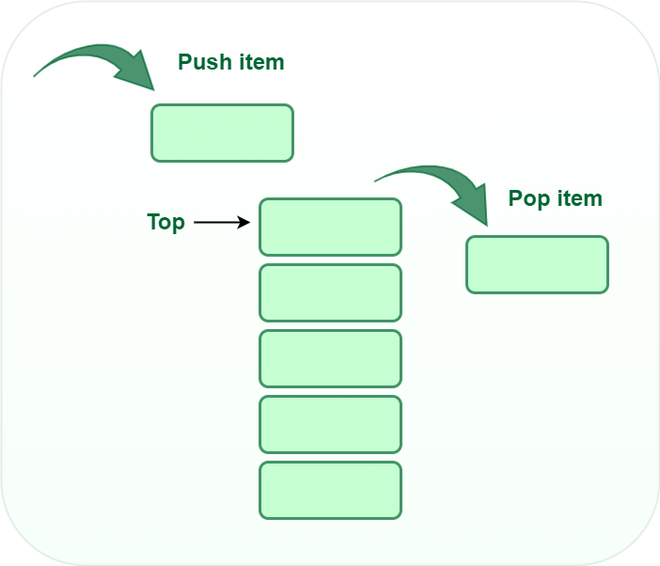
Stack

Time Complexity of Stack Operations:

Operations	Complexity
push()	O(1)
pop()	O(1)
isEmpty()	O(1)
size()	O(1)

Implementation of Stack using Singly Linked List:

To implement a stack using the singly linked list concept, all the singly linked list operations should be performed based on Stack operations LIFO(last in first out) and with the help of that knowledge, we are going to implement a stack using a singly linked list. 

So we need to follow a simple rule in the implementation of a stack which is last in first out and all the operations can be performed with the help of a top variable. Let us learn how to perform Pop, Push, Peek, and Display operations in the following article:

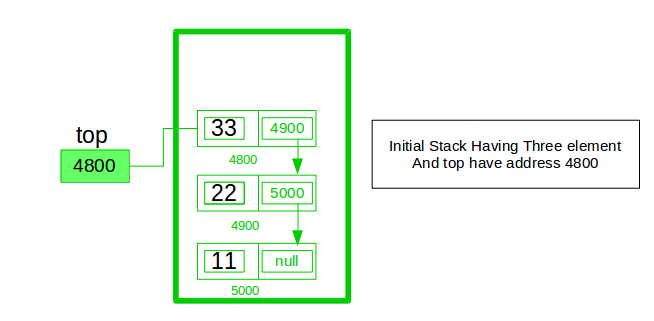
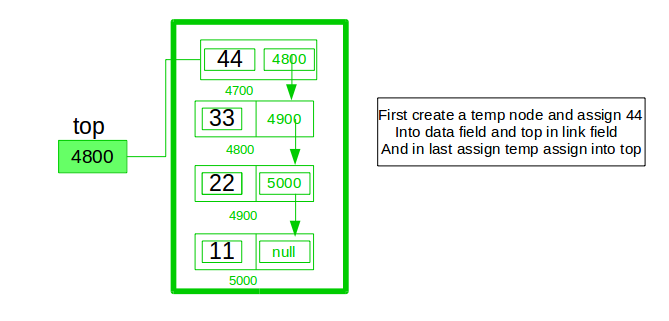
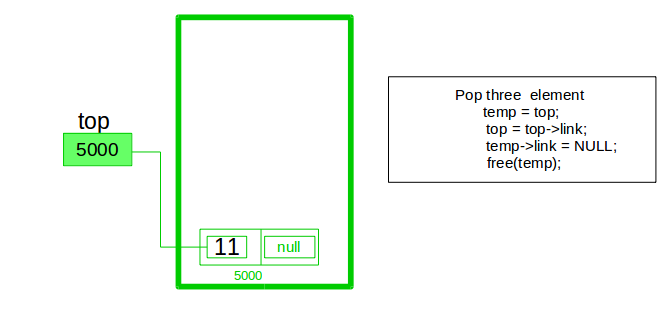
In the stack Implementation, a stack contains a top pointer. which is the “head” of the stack where pushing and popping items happens at the head of the list. The first node has a null in the link field and second node-link has the first node address in the link field and so on and the last node address is in the “top” pointer.

The main advantage of using a linked list over arrays is that it is possible to implement a stack that can shrink or grow as much as needed. Using an array will put a restriction on the maximum capacity of the array which can lead to stack overflow. Here each new node will be dynamically allocated. so overflow is not possible.

Push Operation:

• Initialise a node
• Update the value of that node by data i.e. node->data = data
• Now link this node to the top of the linked list
• And update top pointer to the current node

Pop Operation:

• First Check whether there is any node present in the linked list or not, if not then return
• Otherwise make pointer let say temp to the top node and move forward the top node by 1 step
• Now free this temp node

Peek Operation:

• Check if there is any node present or not, if not then return.
• Otherwise return the value of top node of the linked list

Display Operation:

• Take a temp node and initialize it with top pointer 
• Now start traversing temp till it encounters NULL
• Simultaneously print the value of the temp node

Applications, Advantages and Disadvantages of Stack:

Application of Stack Data Structure:

• Function calls and recursion: When a function is called, the current state of the program is pushed onto the stack. When the function returns, the state is popped from the stack to resume the previous function’s execution.
• Undo/Redo operations: The undo-redo feature in various applications uses stacks to keep track of the previous actions. Each time an action is performed, it is pushed onto the stack. To undo the action, the top element of the stack is popped, and the reverse operation is performed.
• Expression evaluation: Stack data structure is used to evaluate expressions in infix, postfix, and prefix notations. Operators and operands are pushed onto the stack, and operations are performed based on the stack’s top elements.
• Browser history: Web browsers use stacks to keep track of the web pages you visit. Each time you visit a new page, the URL is pushed onto the stack, and when you hit the back button, the previous URL is popped from the stack.
• Balanced Parentheses: Stack data structure is used to check if parentheses are balanced or not. An opening parenthesis is pushed onto the stack, and a closing parenthesis is popped from the stack. If the stack is empty at the end of the expression, the parentheses are balanced.
• Backtracking Algorithms: The backtracking algorithm uses stacks to keep track of the states of the problem-solving process. The current state is pushed onto the stack, and when the algorithm backtracks, the previous state is popped from the stack.

Advantages of Stack:

• Easy implementation: Stack data structure is easy to implement using arrays or linked lists, and its operations are simple to understand and implement.
• Efficient memory utilization: Stack uses a contiguous block of memory, making it more efficient in memory utilization as compared to other data structures.
• Fast access time: Stack data structure provides fast access time for adding and removing elements as the elements are added and removed from the top of the stack.
• Helps in function calls: Stack data structure is used to store function calls and their states, which helps in the efficient implementation of recursive function calls.
• Supports backtracking: Stack data structure supports backtracking algorithms, which are used in problem-solving to explore all possible solutions by storing the previous states.
• Used in Compiler Design: Stack data structure is used in compiler design for parsing and syntax analysis of programming languages.
• Enables undo/redo operations: Stack data structure is used to enable undo and redo operations in various applications like text editors, graphic design tools, and software development environments.

Disadvantages of Stack: 

• Limited capacity: Stack data structure has a limited capacity as it can only hold a fixed number of elements. If the stack becomes full, adding new elements may result in stack overflow, leading to the loss of data.
• No random access: Stack data structure does not allow for random access to its elements, and it only allows for adding and removing elements from the top of the stack. To access an element in the middle of the stack, all the elements above it must be removed.
• Memory management: Stack data structure uses a contiguous block of memory, which can result in memory fragmentation if elements are added and removed frequently.
• Not suitable for certain applications: Stack data structure is not suitable for applications that require accessing elements in the middle of the stack, like searching or sorting algorithms.
• Stack overflow and underflow: Stack data structure can result in stack overflow if too many elements are pushed onto the stack, and it can result in stack underflow if too many elements are popped from the stack.
• Recursive function calls limitations: While stack data structure supports recursive function calls, too many recursive function calls can lead to stack overflow, resulting in the termination of the program.

Infix to Postfix Operation in Stack:

To convert infix expression to postfix expression, use the stack data structure. Scan the infix expression from left to right. Whenever we get an operand, add it to the postfix expression and if we get an operator or parenthesis add it to the stack by maintaining their precedence.

Below are the steps to implement the above idea:

1. Scan the infix expression from left to right. 
2. If the scanned character is an operand, put it in the postfix expression. 
3. Otherwise, do the following
   • If the precedence and associativity of the scanned operator are greater than the precedence and associativity of the operator in the stack [or the stack is empty or the stack contains a ‘(‘ ], then push it in the stack. [‘^‘ operator is right associative and other operators like ‘+‘,’–‘,’*‘ and ‘/‘ are left-associative].
     • Check especially for a condition when the operator at the top of the stack and the scanned operator both are ‘^‘. In this condition, the precedence of the scanned operator is higher due to its right associativity. So it will be pushed into the operator stack. 
     • In all the other cases when the top of the operator stack is the same as the scanned operator, then pop the operator from the stack because of left associativity due to which the scanned operator has less precedence. 
   • Else, Pop all the operators from the stack which are greater than or equal to in precedence than that of the scanned operator.
     • After doing that Push the scanned operator to the stack. (If you encounter parenthesis while popping then stop there and push the scanned operator in the stack.) 
4. If the scanned character is a ‘(‘, push it to the stack. 
5. If the scanned character is a ‘)’, pop the stack and output it until a ‘(‘ is encountered, and discard both the parenthesis. 
6. Repeat steps 2-5 until the infix expression is scanned. 
7. Once the scanning is over, Pop the stack and add the operators in the postfix expression until it is not empty.
8. Finally, print the postfix expression.

Postfix Evaluation using Stack:

To evaluate a postfix expression we can use a stack.

Iterate the expression from left to right and keep on storing the operands into a stack. Once an operator is received, pop the two topmost elements and evaluate them and push the result in the stack again.

Towers of Hanoi using Stack:

Tower of Hanoi is a mathematical puzzle where we have three rods (A, B, and C) and N disks. Initially, all the disks are stacked in decreasing value of diameter i.e., the smallest disk is placed on the top and they are on rod A. The objective of the puzzle is to move the entire stack to another rod (here considered C), obeying the following simple rules: 

• Only one disk can be moved at a time.
• Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.
• No disk may be placed on top of a smaller disk.

Examples:

Input: 3
Output: Disk 1 moved from A to C
Disk 2 moved from A to B
Disk 1 moved from C to B
Disk 3 moved from A to C
Disk 1 moved from B to A
Disk 2 moved from B to C
Disk 1 moved from A to C

Tower of Hanoi using Recursion:

 The idea is to use the helper node to reach the destination using recursion. Below is the pattern for this problem:

• Shift ‘N-1’ disks from ‘A’ to ‘B’, using C.
• Shift last disk from ‘A’ to ‘C’.
• Shift ‘N-1’ disks from ‘B’ to ‘C’, using A.

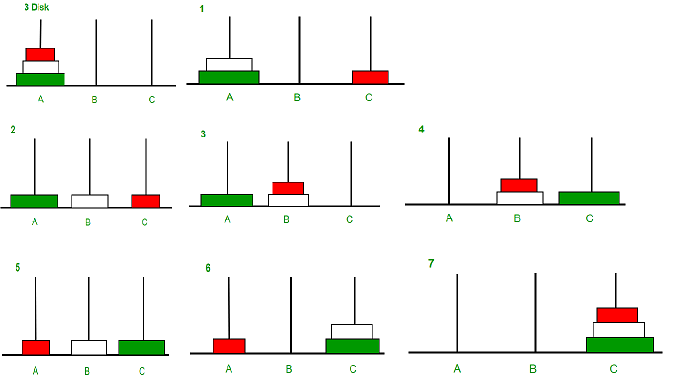
Tower of Hanoi

Follow the steps below to solve the problem:

• Create a function towerOfHanoi where pass the N (current number of disk), from_rod, to_rod, aux_rod.
• Make a function call for N – 1 th disk.
• Then print the current the disk along with from_rod and to_rod
• Again make a function call for N – 1 th disk.

Time complexity: O(2^N), There are two possibilities for every disk. Therefore, 2 * 2 * 2 * . . . * 2(N times) is 2^N
Auxiliary Space: O(N), Function call stack space

Fibonaaci Series using Stack:

The Fibonacci numbers are the numbers in the following integer sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ……..

Fibonacci Series.

Example:

Input  : n = 9

Output : 34

In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation: 

Previously Asked GATE Questions on Stack:

Question 1:

The end of a stack, traditionally known as the position where PUSH and POP operations performed, is known as:

1. FIFO
2. LIFO
3. FRONT
4. TOP

Answer: Option 4 : TOP
Explanation:The top of the stack refers to the end of the stack where operations are performed. This is where elements are added (pushed) and removed (popped). When an element is added to an empty stack, it becomes the top element. When additional elements are pushed onto the stack, they become the new top elements.

Question 2:

What is the equivalent infix expression of the following postfix expression?

M, N, O, +, *, P, /, Q, R, S, T, /, +, *, –

1. N*(M+Q)/Q-P*(S+R/T)
2. (((M*(N+O))/P)-(Q*(R+(S/T))))
3. O * (M + N)/P – Q * (R + S/T)
4. M * (N + O)/Q – P * (R/S + T)

Answer: Option 2 : (((M * (N + O)) / P) – (Q * (R + (S / T))))
Explanation:

Let’s apply this algorithm to the given postfix expression – M, N, O, +, *, P, /, Q, R, S, T, /, +, *, –

Step 1 – Push M, N, O onto the stack Stack – O, N, M

Step 2 – Pop O, N, M and concatenate them with + and * Stack – (M*(N+O))

Step 3 – Push P onto the stack Stack – P, (M*(N+O))

Step 4 – Pop P and concatenate it with / Stack – ((M*(N+O))/P)

Step 5 – Push Q, R, S, T onto the stack Stack – T, S, R, Q, ((M*(N+O))/P)

Step 6 – Pop T, S, R, Q and concatenate them with / and + and * Stack – ((Q*(R+(S/T))), ((M*(N+O))/P)

Step 7 – Pop the final expression from the stack after “-” Infix expression – (((M*(N+O))/P) – ((Q*(R+(S/T))))

Question 3:

What is the postfix representation of the following infix expression?

(A + B) * C – D * E / F

1. A B + C * D E * F – /
2. A B * C + D E * F / –
3. A B + C – D E * F / *
4. A B + C * D E * F / –

Answer: Option 4 : A B + C * D E * F / –
Explanation:

() has highest precedence

* and / has same precedence while + and – has same precedence

(* and /) and higher precedence than (+, -)

Associativity is left to right:

(A + B) * C – D * E / F

A B + * C – D * E / F

A B + C * – D * E / F

A B + C * – D E * / F

A B + C * – D E * F /

A B + C * D E * F / –

Question 4:

The result evaluating the postfix expression 10 5 + 60 6 / * 8 − is

1. 284
2. 213
3. 142
4. 71

Answer: Option 3 : 142

Question 5:

The five items P,Q,R,S and T are pushed in a stack, one after the other starting from P. The stack is popped four times and each element is inserted in a queue. Then two elements are deleted from the queue and pushed back on the stack. now one item is popped from the stack. The popped item is:  

1. P
2. R
3. Q
4. S

Answer: Option 4 : S

Question 6:

Consider the following postfix expression with single digit operands:

6 2 3 * / 4 2 * + 6 8 * –

The top two elements of the stack after second * is evaluated, are:

1. 6, 3
2. 8, 1
3. 8, 2
4. 6, 2

Answer: Option 2 : 8, 1

Question 7:

What is the outcome of the prefix expression +, -, *, 3, 2, /, 8, 4, 1?

1. 12
2. 5
3. 11
4. 4

Answer: Option 2 : 5

Question 8:

A stack is implemented with an array of ‘A [0..N – 1]’ and a variable ‘pos’. The push and pop operations are defined by the following code.

push(x)
                A[pos] ← x
                pos ← pos – 1
end push
pop( )
                pos ← pos + 1
                return A[pos]
end pop

Which of the following will initialize an empty stack with capacity N for the above implementation?

1. pos ← -1
2. pos ← 0
3. pos ← 1
4. pos ← N – 1

Answer: Option 4 : pos ← N – 1

Question 9:

A stack can be implemented using queue, but then we need to use atleast:

1. 3 queues
2. 2 queues
3. only one queue is sufficient
4. none of the options

Answer: Option 2 : 2 queues

Question 10:

Which of the following applications may use a stack?

(a) Parenthesis balancing program

(b) Process scheduling operating system

(c) Conversion of infix arithmetic expression to postfix form

• (a) and (b)
• (b) and (c)
• (a) and (c)
• (a), (b) and (c)

Answer: Option 3 : (a) and (c)