Trees Notes for GATE Exam [2024]

Trees are foundational structures in computer science, serving as the backbone for numerous algorithms and data representations. GATE aspirants should be well versed in tree structures to prepare for the GATE Exam in 2024. This article aims to provide a concise yet comprehensive overview of trees, exploring key concepts crucial for a comprehensive understanding of the topic. To help candidates understand tree-based problem-solving scenarios, these notes provide invaluable insights and knowledge essential to success in GATE.

Introduction to Tree:

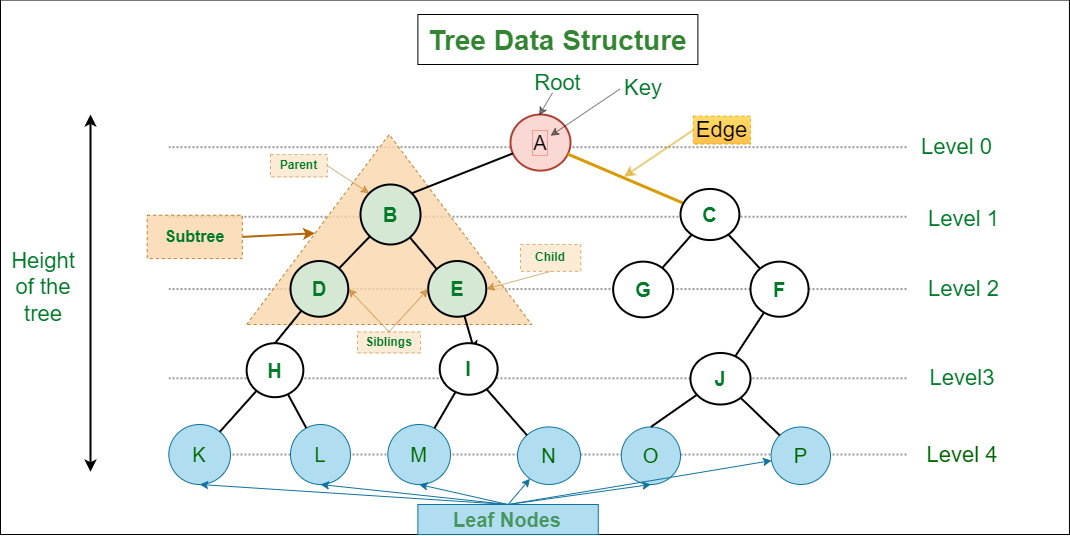
Tree Data Structure is a hierarchical data structure in which a collection of elements known as nodes are connected to each other via edges such that there exists exactly one path between any two nodes.

Basic Terminologies In Tree Data Structure:

• Parent Node: The node which is a predecessor of a node is called the parent node of that node. {B} is the parent node of {D, E}.
• Child Node: The node that is the immediate successor of a node is called the child node of that node. Examples: {D, E} are the child nodes of {B}.
• Root Node: The topmost node of a tree or the node that does not have any parent node is called the root node. {A} is the root node of the tree. A non-empty tree must contain exactly one root node and exactly one path from the root to all other nodes of the tree.
• Leaf Node or External Node: The nodes which do not have any child nodes are called leaf nodes. {K, L, M, N, O, P, G} are the leaf nodes of the tree.
• Ancestor of a Node: Any predecessor nodes on the path of the root to that node are called Ancestors of that node. {A,B} are the ancestor nodes of the node {E}
• Descendant: Any successor node on the path from the leaf node to that node. {E,I} are the descendants of the node {B}.
• Sibling: Children of the same parent node are called siblings. {D,E} are called siblings.
• Level of a node: The count of edges on the path from the root node to that node. The root node has level 0.
• Internal node: A node with at least one child is called Internal Node.
• Neighbour of a Node: Parent or child nodes of that node are called neighbors of that node.
• Subtree: Any node of the tree along with its descendant.

Tree Traversal Techniques:

1. Inorder Traversal:

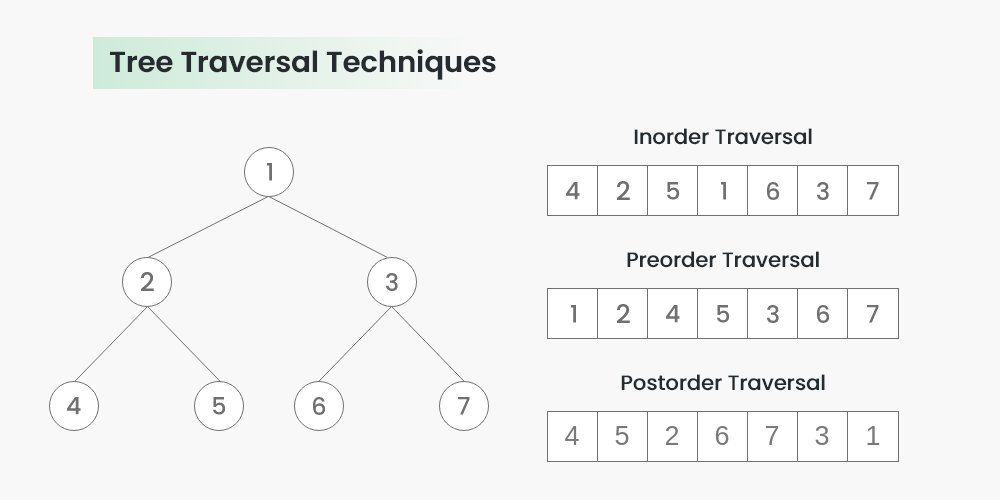
Algorithm Inorder(tree)

• Traverse the left subtree, i.e., call Inorder(left->subtree)
• Visit the root.
• Traverse the right subtree, i.e., call Inorder(right->subtree)

In the case of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order. To get nodes of BST in non-increasing order, a variation of Inorder traversal where Inorder traversal is reversed can be used.

2. Preorder Traversal:

Algorithm Preorder(tree)

• Visit the root.
• Traverse the left subtree, i.e., call Preorder(left->subtree)
• Traverse the right subtree, i.e., call Preorder(right->subtree) 

Preorder traversal is used to create a copy of the tree. Preorder traversal is also used to get prefix expressions on an expression tree.

3. Postorder Traversal:

Algorithm Postorder(tree)

• Traverse the left subtree, i.e., call Postorder(left->subtree)
• Traverse the right subtree, i.e., call Postorder(right->subtree)
• Visit the root

Postorder traversal is used to delete the tree. Postorder traversal is also useful to get the postfix expression of an expression tree

Types of Tree data structures:

Below are types of Tree data structure:

1. Binary Tree
2. Ternary Tree
3. N-ary Tree or Generic Tree
4. Binary Search Tree
5. AVL Tree
6. B-Tree

1. Binary Tree:

In a binary tree, each node can have a maximum of two children linked to it. Some common types of binary trees include full binary trees, complete binary trees, balanced binary trees, and degenerate binary trees.

Below are list of different Binary trees:

• Full Binary Tree: A Binary Tree is a full binary tree if every node has 0 or 2 children. The following are examples of a full binary tree. We can also say a full binary tree is a binary tree in which all nodes except leaf nodes have two children. A full Binary tree is a special type of binary tree in which every parent node/internal node has either two or no children. It is also known as a proper binary tree.
• Degenerate (or pathological) tree: A Tree where every internal node has one child. Such trees are performance-wise same as linked list. A degenerate or pathological tree is a tree having a single child either left or right.
• Skewed Binary Tree: A skewed binary tree is a pathological/degenerate tree in which the tree is either dominated by the left nodes or the right nodes. Thus, there are two types of skewed binary tree: left-skewed binary tree and right-skewed binary tree.
• Complete Binary Tree: A Binary Tree is a Complete Binary Tree if all the levels are completely filled except possibly the last level and the last level has all keys as left as possible.
• Perfect Binary Tree A Binary tree is a Perfect Binary Tree in which all the internal nodes have two children and all leaf nodes are at the same level. 
  Balanced Binary Tree A binary tree is balanced if the height of the tree is O(Log n) where n is the number of nodes. For Example, the AVL tree maintains O(Log n) height by making sure that the difference between the heights of the left and right subtrees is at most 1.

2. Ternary Tree:

A Ternary Tree is a tree data structure in which each node has at most three child nodes, usually distinguished as “left”, “mid” and “right”.

3. N-ary Tree or Generic Tree:

Generic trees are a collection of nodes where each node is a data structure that consists of records and a list of references to its children(duplicate references are not allowed). Unlike the linked list, each node stores the address of multiple node.

4. Binary Search Tree:

Binary Search Tree is a node-based binary tree data structure which has the following properties:

• The left subtree of a node contains only nodes with keys lesser than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• The left and right subtree each must also be a binary search tree.

Operations in an BST:

1. Insertion in BST:
2. Searching in BST:
3. Deletion in BST:

4.1 Insertion in BST:

A new key is always inserted at the leaf by maintaining the property of the binary search tree. We start searching for a key from the root until we hit a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node. The below steps are followed while we try to insert a node into a binary search tree:

• Check the value to be inserted (say X) with the value of the current node (say val) we are in:
  • If X is less than val move to the left subtree.
  • Otherwise, move to the right subtree.
• Once the leaf node is reached, insert X to its right or left based on the relation between X and the leaf node’s value.

Time Complexity: O(h) where h is the height of the Binary Search Tree. In the worst case, we may have to travel from the root to the deepest leaf node. The height of a skewed tree may become n and the time complexity of insertion operation may become O(n). 
Auxiliary Space: O(1), if we use a iterative approach, and (n), as we use recursive approach.

4.2 Searching in BST:

For searching a value in BST, consider it as a sorted array. Now we can easily perform search operation in BST using Binary Search Algorithm. Let’s say we want to search for the number X, We start at the root. Then:

• We compare the value to be searched with the value of the root. 
  • If it’s equal we are done with the search if it’s smaller we know that we need to go to the left subtree because in a binary search tree all the elements in the left subtree are smaller and all the elements in the right subtree are larger. 
• Repeat the above step till no more traversal is possible
• If at any iteration, key is found, return True. Else False.

Time Complexity: O(h), where h is the height of the BST.
Auxiliary Space:The auxiliary space complexity of searching in a binary search tree is O(1) if we use a iterative approach, and (n), as we use recursive approach.

4.3 Deletion in BST:

The task to delete a node in this BST, can be broken down into 3 scenarios:

Case 1. Delete a Leaf Node in BST

If the node to be deleted is a leaf node, it can simply be removed from the tree. The parent node of the deleted node must have its corresponding child pointer set to NULL to reflect the change in the tree.

Case 2. Delete a Node with Single Child in BST

If the node to be deleted has only one child, the child can be promoted to replace the deleted node. The parent node of the deleted node must have its corresponding child pointer updated to point to the promoted child.

Case 3. Delete a Node with Both Children in BST

If the node to be deleted has two children, the replacement node can be found by either selecting the minimum value from the right subtree or the maximum value from the left subtree of the node to be deleted. After finding the replacement node, it can be promoted to replace the deleted node. The left subtree of the replacement node (if it exists) must be attached to the left child of the promoted node, and the right subtree of the replacement node (if it exists) must be attached to the right child of the promoted node. The parent node of the deleted node must have its corresponding child pointer updated to point to the promoted node.

Time Complexity: O(h), where h is the height of the BST. 
Auxiliary Space: O(n).

6. AVL Tree

An AVL tree defined as a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees for any node cannot be more than one.

The difference between the heights of the left subtree and the right subtree for any node is known as the balance factor of the node.

Rotating the subtrees in an AVL Tree:

An AVL tree may rotate in one of the following four ways to keep itself balanced:

Left Rotation:

When a node is added into the right subtree of the right subtree, if the tree gets out of balance, we do a single left rotation.

Right Rotation:

If a node is added to the left subtree of the left subtree, the AVL tree may get out of balance, we do a single right rotation.

Left-Right Rotation:

A left-right rotation is a combination in which first left rotation takes place after that right rotation executes.

Right-Left Rotation:

A right-left rotation is a combination in which first right rotation takes place after that left rotation executes.

Operations in an AVL Tree:

• Insertion
• Deletion
• Searching

Previously Asked GATE Questions on Trees:

Question 1: Let LASTPOST, LASTIN and LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal. Respectively, of a complete binary tree. Which of the following is always true? (GATE CS 2000) 
(a) LASTIN = LASTPOST 
(b) LASTIN = LASTPRE 
(c) LASTPRE = LASTPOST 
(d) None of the above 

Answer: (d) 

Explanation: It is given that the given tree is complete binary tree. For a complete binary tree, the last visited node will always be same for inorder and preorder traversal. None of the above is true even for a complete binary tree. 

The option (a) is incorrect because the last node visited in Inorder traversal is right child and last node visited in Postorder traversal is root. 

The option (c) is incorrect because the last node visited in Preorder traversal is right child and last node visited in Postorder traversal is root. 

For option (b), see the following counter example.

     1
   /    \
  2      3
 / \    /
4   5  6  

Inorder traversal is 4 2 5 1 6 3
Preorder traversal is 1 2 4 5 3 6 

Question 2: The most appropriate matching for the following pairs is (GATE CS 2000): :

X: depth first search 1: heap
Y: breadth-first search 2: queue
Z: sorting 3: stack

(a) X—1 Y—2 Z-3 
(b) X—3 Y—1 Z-2 
(c) X—3 Y—2 Z-1 
(d) X—2 Y—3 Z-1 

Answer: (c) 

Explanation: Stack is used for Depth first Search 
Queue is used for Breadth First Search 
Heap is used for sorting 

Question 3: Consider the following nested representation of binary trees: (X Y Z) indicates Y and Z are the left and right sub stress, respectively, of node X. Note that Y and Z may be NULL, or further nested. Which of the following represents a valid binary tree? 
(a) (1 2 (4 5 6 7)) 
(b) (1 (2 3 4) 5 6) 7) 
(c) (1 (2 3 4)(5 6 7)) 
(d) (1 (2 3 NULL) (4 5)) 

Answer: (c) 

Question 4: Consider the label sequences obtained by the following pairs of traversals on a labeled binary tree. Which of these pairs identify a tree uniquely (GATE CS 2004)?
i) preorder and postorder
ii) inorder and postorder
iii) preorder and inorder
iv) level order and postorder

a) (i) only
b) (ii), (iii)
c) (iii) only
d) (iv) only

Answer: (b)

Question 5: The following numbers are inserted into an empty binary search tree in the given order: 10, 1, 3, 5, 15, 12, 16. What is the height of the binary search tree (the height is the maximum distance of a leaf node from the root)? (GATE CS 2004)
a) 2
b) 3
c) 4
d) 6

Answer: (b)
Explanation: Constructed binary search tree will be..

10
/ \
1 15
\ / \
3 12 16
\
5

Question 6: A data structure is required for storing a set of integers such that each of the following operations can be done in (log n) time, where n is the number of elements in the set.

o Deletion of the smallest element
o Insertion of an element if it is not already present in the set

Which of the following data structures can be used for this purpose?
(a) A heap can be used but not a balanced binary search tree
(b) A balanced binary search tree can be used but not a heap
(c) Both balanced binary search tree and heap can be used
(d) Neither balanced binary search tree nor heap can be used

Answer: (b)

Explanation: A self-balancing balancing binary search tree containing n items allows the lookup, insertion, and removal of an item in O(log n) worst-case time. Since it’s a self-balancing BST, we can easily find out minimum element in O(logn) time which is always the leftmost element (See Find the node with the minimum value in a Binary Search Tree).

Since Heap is a balanced binary tree (or almost complete binary tree), insertion complexity for heap is O(logn). Also, complexity to get minimum in a min heap is O(logn) because removal of root node causes a call to heapify (after removing the first element from the array) to maintain the heap tree property. But a heap cannot be used for the above purpose as the question says – insert an element if it is not already present. For a heap, we cannot find out in O(logn) if an element is present or not. Thanks to the game for providing the correct solution.

Question 7: The height of a binary tree is the maximum number of edges in any root to leaf path. The maximum number of nodes in a binary tree of height h is:
(a) 2^h -1
(b) 2^(h-1) – 1
(c) 2^(h+1) -1
(d) 2*(h+1)

Answer: (c)

Explanation: Maximum number of nodes will be there for a complete tree. Number of nodes in a complete tree of height h = 1 + 2 + 2^2 + 2*3 + …. 2^h = 2^(h+1) – 1

Question 8: The inorder and preorder traversal of a binary tree are d b e a f c g and a b d e c f g, respectively. The postorder traversal of the binary tree is:
(a) d e b f g c a
(b) e d b g f c a
(c) e d b f g c a
(d) d e f g b c a

Answer: (a)

Below is the given tree.

a

/ \

/ \

b c

/ \ / \

/ \ / \

d e f g

Question 9: A complete n-ary tree is a tree in which each node has n children or no children. Let I be the number of internal nodes and L be the number of leaves in a complete n-ary tree. If L = 41, and I = 10, what is the value of n? 
(a) 3 
(b) 4 
(c) 5 
(d) 6

Answer: (c) 
For an n-ary tree where each node has n children or no children, following relation holds 

L = (n-1)*I + 1

Where L is the number of leaf nodes and I is the number of internal nodes.
Let us find out the value of n for the given data. 

L = 41 , I = 10
41 = 10*(n-1) + 1
(n-1) = 4
n = 5

Question 10: What is the number of binary search trees with 20 nodes with elements 1, 2, 3,…..20 such that the root of tree is 12 and the root of left subtree is 7? 
(a) 2634240 
(b) 1243561 
(c) 350016 
(d) 2642640 

Answer: (d) 

Explanation:
Number of nodes in left subtree = 11 {1, 2, 3, 4….11} 
Number of nodes in the right subtree = 8 {13, 14, ….20} 
Since for the left subtree root is 7 
Number of elements in the left part of left subtree = 6 {1, 2, 3..6} 
Number of elements in the right part of left subtree = 4 {8, 9, 10, 11} 
We know number of Binary Search trees with n nodes = (C(2n,n)/n+1) 
Number of BST with 6 nodes = (C(12,6)/7) = 132 
Number of BST with 4 nodes = (C(8,4)/5) = 14 
Number of BST with 8 nodes = (C(16,8)/9) =1430 
Total number of BST = 2642640