Python | Mean Squared Error
Last Updated :
30 Jun, 2019
The
Mean Squared Error (MSE) or
Mean Squared Deviation (MSD) of an estimator measures the average of error squares i.e. the average squared difference between the estimated values and true value. It is a risk function, corresponding to the expected value of the squared error loss. It is always non – negative and values close to zero are better. The MSE is the second moment of the error (about the origin) and thus incorporates both the variance of the estimator and its bias.
Steps to find the MSE
- Find the equation for the regression line.
(1) 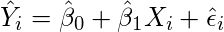
- Insert X values in the equation found in step 1 in order to get the respective Y values i.e.
(2) 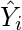
- Now subtract the new Y values (i.e.
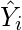 ) from the original Y values. Thus, found values are the error terms. It is also known as the vertical distance of the given point from the regression line.
) from the original Y values. Thus, found values are the error terms. It is also known as the vertical distance of the given point from the regression line.
(3) 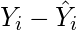
- Square the errors found in step 3.
(4) 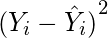
- Sum up all the squares.
(5) 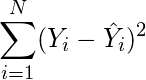
- Divide the value found in step 5 by the total number of observations.
(6) 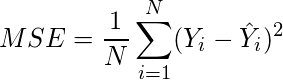
Example:
Consider the given data points: (1,1), (2,1), (3,2), (4,2), (5,4)
You can use
this online calculator to find the regression equation / line.
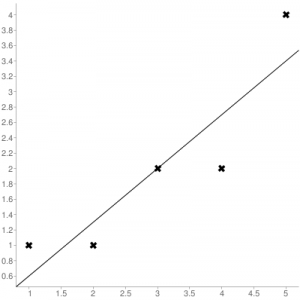 Regression line equation: Y = 0.7X – 0.1
Regression line equation: Y = 0.7X – 0.1
| X |
Y |
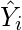 |
| 1 |
1 |
0.6 |
| 2 |
1 |
1.29 |
| 3 |
2 |
1.99 |
| 4 |
2 |
2.69 |
| 5 |
4 |
3.4 |
Now, using formula found for
MSE in step 6 above, we can get
MSE = 0.21606
MSE using scikit – learn:
from sklearn.metrics import mean_squared_error
Y_true = [1,1,2,2,4]
Y_pred = [0.6,1.29,1.99,2.69,3.4]
mean_squared_error(Y_true,Y_pred)
|
Output: 0.21606
MSE using Numpy module:
import numpy as np
Y_true = [1,1,2,2,4]
Y_pred = [0.6,1.29,1.99,2.69,3.4]
MSE = np.square(np.subtract(Y_true,Y_pred)).mean()
|
Output: 0.21606
Share your thoughts in the comments
Please Login to comment...