R-squared in Regression Analysis in Machine Learning
Last Updated :
10 May, 2023
The most important thing we do after making any model is evaluating the model. We have different evaluation matrices for evaluating the model. However, the choice of evaluation matrix to use for evaluating the model depends upon the type of problem we are solving whether it’s a regression, classification, or any other type of problem. In this article, we will explain R-Square for regression analysis problems.
What is R-Squared
R-squared is a statistical measure that represents the goodness of fit of a regression model. The value of R-square lies between 0 to 1. Where we get R-square equals 1 when the model perfectly fits the data and there is no difference between the predicted value and actual value. However, we get R-square equals 0 when the model does not predict any variability in the model and it does not learn any relationship between the dependent and independent variables.
How is R-Squared Calculated
R-squared also known as the coefficient of determination measures the variability in the dependent variable Y that is being explained by the independent variables Xi in the regression model.
We calculate R-Square in the following steps
- First, calculate the mean of the target/dependent variable y and we denote it by y̅
- Calculate the total sum of squares by subtracting each observation yi from y̅, then squaring it and summing these square differences across all the values. It is denoted by
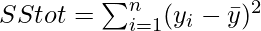
- We estimate the model parameter using a suitable regression model such as Linear Regression or SVM Regressor
- We calculate the Sum of squares due to regression which is denoted by SSR. This is calculated by subtracting each predicted value of y denoted by y_predi from yi squaring these differences and then summing all the n terms. SSR = \sum_{i=1}^{n} (\hat{ypred}_i – \bar{y})^2
- We calculate the sum of squares (SSres). It explains unaccounted variability in the dependent y after predicting these values from an independent variable in the model. SSres = \sum_{i=1}^n (y_i – {ypred}_i)^2
- we can then use either
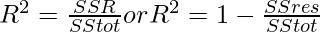
R-Squared Goodness Of Fit
R-square is a comparison of the residual sum of squares (SSres) with the total sum of squares(SStot). The total sum of squares is calculated by summation of squares of perpendicular distance between data points and the average line. 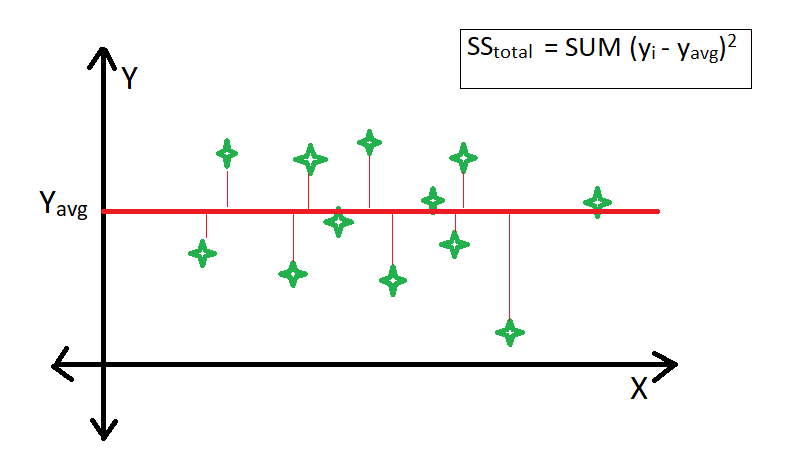
The residual sum of squares is calculated by the summation of squares of perpendicular distance between data points and the best-fitted line.
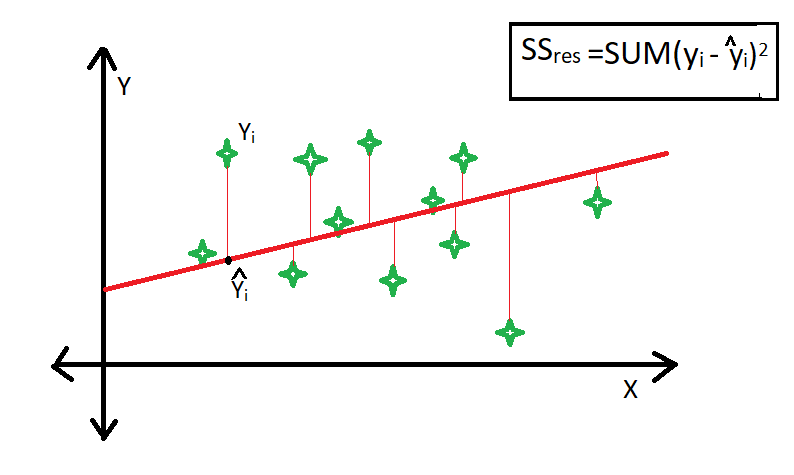
R square is calculated by using the following formula :
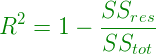
Where SSres is the residual sum of squares and SStot is the total sum of squares.
The goodness of fit of regression models can be analyzed on the basis of the R-square method. The more the value of the r-square near 1, the better the model is.
Note: The value of R-square can also be negative when the model fitted is worse than the average fitted model.
Limitation of using the R-square method –
- The value of r-square always increases or remains the same as new variables are added to the model, without detecting the significance of this newly added variable (i.e. the value of r-square never decreases on the addition of new attributes to the model). As a result, non-significant attributes can also be added to the model with an increase in the r-square value.
- This is because SStot is always constant and the regression model tries to decrease the value of SSres by finding some correlation with this new attribute hence the overall value of r-square increases, which can lead to a poor regression model.
R-Squared Vs Adjusted R-Squared
Adjusted R-Squared is an updated version of R-squared which takes account of the number of independent variables while calculating R-squared. The main problem with R-squared is that the R-Square value always increases with an increase in independent variables irrespective of the fact that where the independent variable is contributing to the model or not. This leads to the model having high variance if the model has a lot of independent variables.
Formula For Adjusted R-Squared
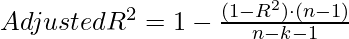
- Here R-square is the value that we calculate using the method explained above
- n is the total number of observations in the data
- k is the number of independent variables (predictors) in the regression model
Share your thoughts in the comments
Please Login to comment...