ML | Momentum-based Gradient Optimizer introduction

Gradient Descent is an optimization technique used in Machine Learning frameworks to train different models. The training process consists of an objective function (or the error function), which determines the error a Machine Learning model has on a given dataset. 
While training, the parameters of this algorithm are initialized to random values. As the algorithm iterates, the parameters are updated such that we reach closer and closer to the optimal value of the function.

However, Adaptive Optimization Algorithms are gaining popularity due to their ability to converge swiftly. All these algorithms, in contrast to the conventional Gradient Descent, use statistics from the previous iterations to robustify the process of convergence.

Momentum-based Gradient Optimizer is a technique used in optimization algorithms, such as Gradient Descent, to accelerate the convergence of the algorithm and overcome local minima. In the Momentum-based Gradient Optimizer, a fraction of the previous update is added to the current update, which creates a momentum effect that helps the algorithm to move faster towards the minimum.

The momentum term can be viewed as a moving average of the gradients. The larger the momentum term, the smoother the moving average, and the more resistant it is to changes in the gradients. The momentum term is typically set to a value between 0 and 1, with a higher value resulting in a more stable optimization process.

The update rule for the Momentum-based Gradient Optimizer can be expressed as follows:

makefile
v = beta * v - learning_rate * gradient
parameters = parameters + v

// Where v is the velocity vector, beta is the momentum term, 
// learning_rate is the step size, 
// gradient is the gradient of the cost function with respect to the parameters, 
// and parameters are the parameters of the model.

The Momentum-based Gradient Optimizer has several advantages over the basic Gradient Descent algorithm, including faster convergence, improved stability, and the ability to overcome local minima. It is widely used in deep learning applications and is an important optimization technique for training deep neural networks.

Momentum-based Optimization:

An Adaptive Optimization Algorithm uses exponentially weighted averages of gradients over previous iterations to stabilize the convergence, resulting in quicker optimization. For example, in most real-world applications of Deep Neural Networks, the training is carried out on noisy data. It is, therefore, necessary to reduce the effect of noise when the data are fed in batches during Optimization. This problem can be tackled using Exponentially Weighted Averages (or Exponentially Weighted Moving Averages).

Implementing Exponentially Weighted Averages:

In order to approximate the trends in a noisy dataset of size N: 
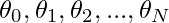, we maintain a set of parameters 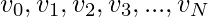. As we iterate through all the values in the dataset, we calculate the parameters below: 

On iteration t:
    Get next 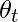[Tex]v_{\theta} = \beta v_{\theta} + (1 - \beta) \theta_{t}[/Tex]

This algorithm averages the value of 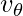over its values from previous 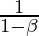iterations. This averaging ensures that only the trend is retained and the noise is averaged out. This method is used as a strategy in momentum-based gradient descent to make it robust against noise in data samples, resulting in faster training.

As an example, if you were to optimize a function on the parameter x, the following pseudo-code illustrates the algorithm:

On iteration t:
    On the current batch, compute [Tex]v := v + (1 - \beta) \frac{\partial f(x)}{\partial x}[/Tex]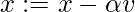

The HyperParameters for this Optimization Algorithm are 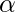, called the Learning Rate and, 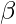, similar to acceleration in mechanics.

Implementation:

Following is an implementation of Momentum-based Gradient Descent on a function :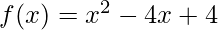  

Python3

import math

# HyperParameters of the optimization algorithm
alpha = 0.01
beta = 0.9

# Objective function


def obj_func(x):
    return x * x - 4 * x + 4

# Gradient of the objective function


def grad(x):
    return 2 * x - 4


# Parameter of the objective function
x = 0

# Number of iterations
iterations = 0

v = 0

while (1):
    iterations += 1
    v = beta * v + (1 - beta) * grad(x)

    x_prev = x

    x = x - alpha * v

    print("Value of objective function on iteration", iterations, "is", x)

    if x_prev == x:
        print("Done optimizing the objective function. ")
        break

Output

...999999938
Value of objective function on iteration 1261 is 1.999999999999994
Value of objective function on iteration 1262 is 1.9999999999999942
Value of objective function on iteration 1263 is 1.9999999999999944
Value of objective function on iteration 1264 is 1.9999999999999947
Value of objective function on iteration 1265 is 1.999999999999995
Value of objective function on iteration 1266 is 1.9999999999999951
Value of objective function on iteration 1267 is 1.9999999999999953
Value of objective function on iteration 1268 is 1.9999999999999956
Value of objective function on iteration 1269 is 1.9999999999999958
Value of objective function on iteration 1270 is 1.999999999999996
Value of objective function on iteration 1271 is 1.9999999999999962
Value of objective function on iteration 1272 is 1.9999999999999964
Value of objective function on iteration 1273 is 1.9999999999999967
Value of objective function on iteration 1274 is 1.9999999999999967
Done optimizing the objective function.