Moment of Inertia

Moment of inertia is the property of a body in rotational motion. It is similar to the inertia of any body in translational motion. Moment of Inertia is the property of the rotational bodies which tends to oppose the change in rotational motion of the body. Mathematically, the Moment of Inertia is given as the sum of the product of the mass of each particle and the square of the distance from the rotational axis. Let’s learn about the Moment of Inertia in detail in the article below.

Moment of Inertia Definition

Moment of Inertia is the tendency of a body in rotational motion which opposes the change in its rotational motion due to external forces. The Moment of Inertia behaves as angular mass and is called rotational inertia. Moment of Inertia is analogous to the mechanical Inertia of the body.

MOI is defined as the quantity expressed by the sum of the product of the mass of every particle with the square of its distance from the axis of rotation for any particle performing the rotational motion.

Unit of Moment of Inertia

Moment of Inertia is a scalar quantity and the SI unit of the Moment of Inertia is kgm².

Moment of Inertia Dimensional Formula

Since the Moment of Inertia is given as the product of mass and square of distance. Its dimensional formula is given by the product of the dimensional formula of mass and the square of the dimensional formula of length. The dimensional formula of the moment of inertia is, ML²

What is Inertia?

Inertia is the property of a matter by virtue of which it tends to resist the change in the state of its motion. This means a body in rest tries to remain at rest and resist any force trying to bring it into motion, and a body in motion tries to continue in motion and resist any force trying to bring it to change the magnitude of its motion. In terms of quantity, it is equal to the maximum force trying to change its state of motion.

Learn more about Inertia.

Moment of Inertia Formula

The Moment of Inertia is a scalar quantity. Mathematically, the product of the square of the mass of a particle and the distance from the axis of rotation is called the moment of inertia of the particle about the axis of rotation.

The general formula for finding the Moment of Inertia of any object is,

I = mr²

where,
m is the mass of the object’
r is the distance from the axis of rotation

For a body of consisting of continuous infinitesimally small particles, the Integral form of the Moment of Inertia is used to calculate the Moment of Inertia.

I = ∫dI

I =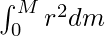 

Moment of Inertia of a System of Particles

Moment of Inertia of a system of particles is given by the formula,

I = ∑m_i r_i²

where,
r_i is the perpendicular distance of the i^th particle from the axis
m_i is the mass of i^th particle

The above Moment of Inertia equation tells that moment of inertia for a system of particles is equal to the sum of product of the mass of each and the square of the distance from the rotation axis of each particle.

For the figure given below,

Moment of inertia of first particle = m₁×r₁²

Moment of inertia of second particle = m₂×r₂²

Moment of inertia of third particle = m₃×r₃² 

Similarly, 

Moment of inertia of n^th particle = m_n×r_n²

Now the moment of inertia of the entire body about the axis of rotation AB will be equal to the sum of the moment of inertia of all the particles, so

I = m₁×r₁² + m₂×r₂² + m₃×r₃²  +……+m_n×r_n²

I = Σ m_i×r_i²

where,
I represent moment of inertia of the body about the axis of rotation
m_i is the mass of i^th particle,
r_i is the radius of i^th particle
Σ represents the sum. 

From the equation, we can say that the moment of inertia of a body about a fixed axis is equal to the sum of the product of the mass of each particle of that body and the square of its perpendicular distance from the fixed axis.

Factors Affecting Moment of Inertia

Moment of Inertia of any object depends on the following values:

• Shape and size of the object
• Density of the material of the object
• Axis of Rotation

How to Calculate Moment Of Inertia?

Several ways are used to calculate the moment of inertia of any rotating object. 

• For uniform objects, the moment of inertia is calculated by taking the product of its mass with the square of its distance from the axis of rotation (r²). 
• For non-uniform objects, we calculate the moment of inertia by taking the sum of the product of individual point masses at each different radius for this the formula used is

I = ∑m_ir_i²

Moment Of Inertia Formula for Different Shapes

This table discusses expressions for the moment of inertia for some symmetric objects along with their rotation axis:

Object	Axis	Expression of the Moment of Inertia
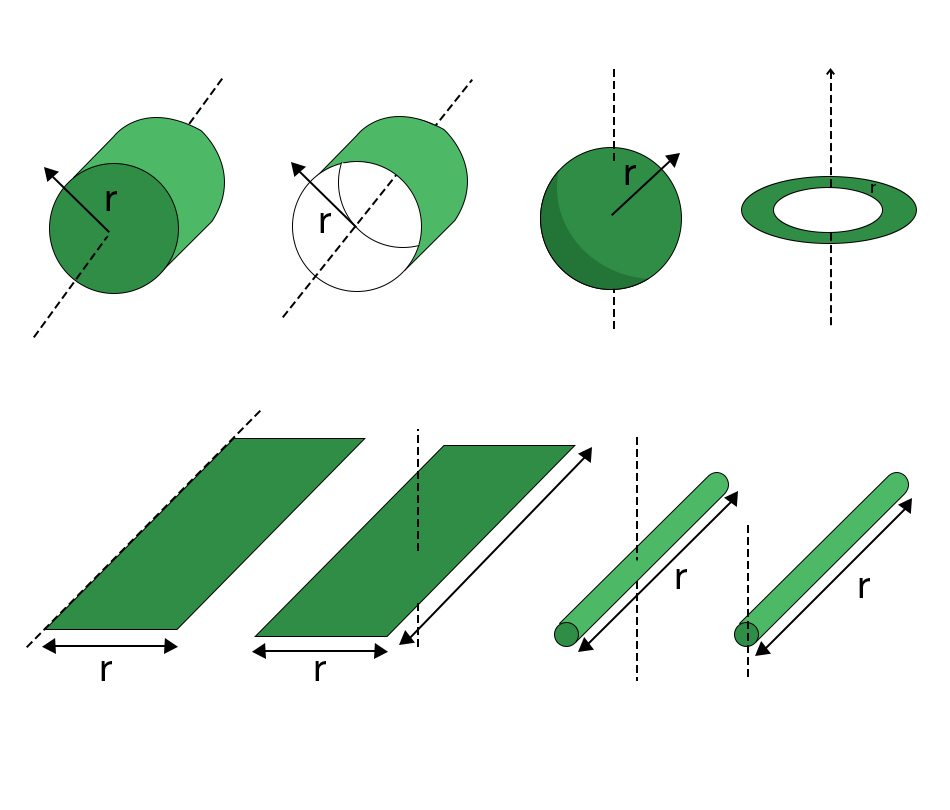
Hollow Cylinder Thin-walled	Central	I = Mr2
Thin Ring	Diameter	I = 1/2 Mr2
Annular Ring or Hollow Cylinder	Central	I = 1/2 M(r22 + r12)
Solid Cylinder	Central	I = 1/2 Mr2
Uniform Disc	Diameter	I = 1/4 Mr2
Hollow Sphere	Central	I = 2/3 Mr2
Solid Sphere	Central	I = 2/5 Mr2
Uniform Symmetric Spherical Shell	Central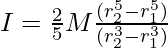
Uniform Plate or Rectangular Parallelepiped	Central	I = 1/12 M(a2 + b2)
Thin rod	Central	I = 1/12 Mr2
Thin rod	At the End of Rod	I = 1/3 Mr2

Radius of Gyration

The Radius of Gyration of a body is defined as the perpendicular distance from the axis of rotation to the point of mass whose mass is equal to the mass of the whole body and the Moment of Inertia is equal to the actual moment of inertia of the object as it has been assumed that total mass of the body is concentrated there. It is an imaginary distance. The Radius of Gyration is denoted by K.

If the mass and radius of gyration of the body are M and K respectively, then the moment of inertia of a body is

I = MK² ……(1)

Thus, the Radius of Gyration of a body is perpendicular to the axis of rotation whose square multiplied by the mass of that body gives the moment of inertia of that body about that axis.

Again by equation (1), K² = I/M

K = √(I/m)

Thus, the Radius of the Gyration of a body about an axis is equal to the square root of the ratio of the body about that axis.

Moment of Inertia Theorems

There are two types of theorems that are very important with respect to the Moment of Inertia:

• Parallel Axis Theorem
• Perpendicular Axis Theorem

Perpendicular Axis Theorem

The sum of the moment of inertia of a body about two mutually perpendicular axes situated in the plane of a body is equal to the moment of inertia of the body about the third axis which is perpendicular to the two axes and passes through their point of intersection.

In the above figure, OX and OY are two axes in the plane of the body which are perpendicular to each other. The third axis is OZ which is perpendicular to the plane of the body and passes through the point of intersection of the OX and OY axes. If I_x, I_y, and I_z are the moments of inertia of the body about the axis OX, OY, and OZ axes respectively, then according to this theorem

I_x + I_y = I_z

Parallel Axis Theorem

According to this theorem, the moment of inertia of a body about a given axis is the sum of the moment of inertia about an axis passing through the center of mass of that body and the product of the square of the mass of the body and the perpendicular distance between the two axes.

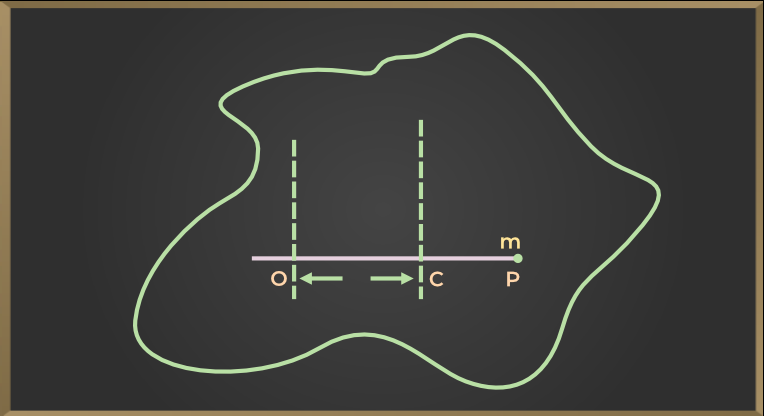
Let in the above figure, we have to find the moment of inertia of I_O of the body passing through the point O and about the axis perpendicular to the plane, while the moment of inertia of the body passing through the center of mass C and about an axis parallel to the given axis is I_C, then according to this theorem

I_O = I_C + Ml²

where 
M is the mass of the entire body
l is the perpendicular distance between two axes.

Moments of Inertia for Different Objects

Moment of Inertia of different objects is discussed below in this article

Moment of Inertia of a Rectangular Plate

If the mass of the plate is M, length l, and width b, then the moment of inertia passes through the center of gravity and about an axis perpendicular to the plane of the plate.

I = M(l² + b² / 12)

Moment of Inertia of a Disc

If the disc has a mass M and radius r, then the moment of inertia about the disc’s geometric axis is

I = 1/2(Mr²)

Moment of Inertia of a Rod

If the mass of the rod is M and the length is l, then the moment of inertia about the axis perpendicular to the length of the rod and passing through its center of gravity

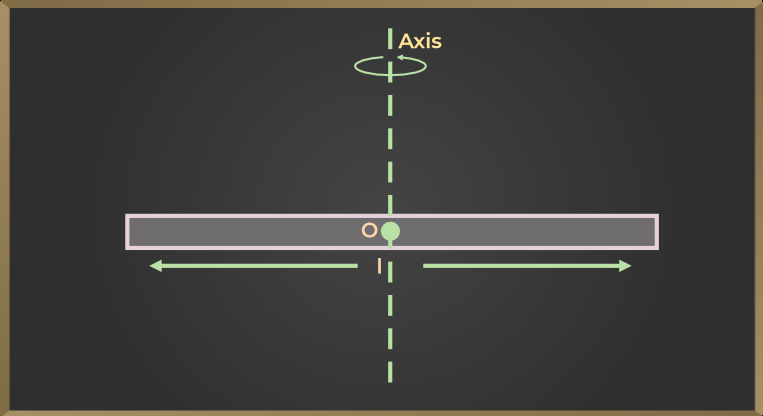
I = ML²/12

Moment of Inertia of a Circle

If the mass of the ring is M and the radius of the ring is r, then the moment of inertia about the axis passing through perpendicularly to the center of the ring is

I = Mr²

Moment of Inertia of a Sphere

If a Solid Sphere has a mass of M and a radius of r, then the moment of inertia about its diameter is

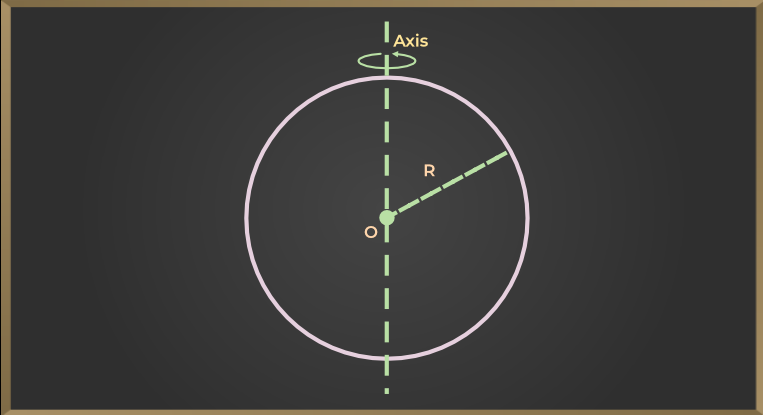
I = 2/5Mr²

Moment of Inertia of Solid Cylinder

The Moment of Inertia of a Solid Cylinder of Radius ‘R’ and mass M is given by

I = 1/2MR²

Moment of Inertia of Hollow Cylinder

A hollow cylinder has two radii namely internal radius and external radius. The Moment of Inertia of a Hollow Cylinder having mass M, external radius R₁, and internal radius R₂ is given as

I = 1/2M(R₁² + R₂²)

Moment of Inertia of Solid Sphere

The Moment of Inertia of a Solid Sphere of Mass ‘M’ and Radius ‘R’ is given as

I = 2/5MR²

Moment of Inertia of Hollow Sphere

The Moment of Inertia of a Hollow Sphere of Mass M and Radius ‘R’ is given as

I = 2/3MR²

Moment of Inertia of Ring

The Moment of Inertia of a Ring is given for two cases when the axis of rotation passes through center and when the axis of rotation passes through the diameter.

The Moment of Inertia of the Ring about the axis passing through the center is given by

I = MR²

The Moment of Inertia of the Ring about the axis passing through the diameter is given by

I = Mr²/2

Moment of Inertia of Square

The Moment of Inertia of the Square of side ‘a’ is given as

I = a⁴/12

The Moment of Inertia of a Square Plate of the Side of length ‘l’ and mass M is given as

I = 1/6ML²

Moment of Inertia of Triangle

The Moment of Inertia of a Triangle is given for 3 situations, first, when axis pass through the centre, second when axis pass through the base and third when axis is perpendicular to the base. Let’s see the formula for them one by one. For a triangle of base ‘b’ and height ‘h’, the formula for moment of inertia is given as follows

When axis pass though the Centroid

I = bh³/36

When axis pass through the Base

I = bh³/12

When axis is Perpendicular to the base

I = (hb/36)(b² – b₁b + b₁²)

Difference Between Moment of Inertia and Inertia

S.No.	Inertia	Moment of Inertia
1.	Its importance is in linear motion.	Its importance is in rotational motion.
2.	It is that property of an object which opposes the change of state of the object in linear motion.	The moment of inertia is that property of an object which opposes the change of state of the object in rotational motion.
3.	The inertia of an object depends only on its mass.	The moment of inertia of an object depends on its mass and its mass distribution relative to the axis of rotation.
4.	The inertia of an object is fixed.	The moment of inertia of an object varies with respect to different axes of rotation.

Kinetic Energy of Rotating Body

Let us assume a body of Mass ‘m’ rotating with velocity v at a distance ‘r’ from the axis of rotation. Its angular velocity is then given by ω = v/r then v = rω. Now we know that the Kinetic Energy of a body is given by

KE = 1/2mv²

⇒ KE = 1/2m(rω)²

⇒ KE = 1/2mr²ω²

⇒ KE = 1/2Iω²

Hence, the Kinetic Energy of a Rotating Body is given by half of the product of the Moment of Inertia and the angular velocity of the body.

KE = 1/2Iω²

The Moment of Inertia(I) is independent of the angular velocity of the body. It is a function of the mass of the rotating body and the distance of the body from the axis of rotation. Hence, we observe that angular motion is analogous to linear motion, this means that the significance of Moment of Inertia is that it gives an idea about how masses are distributed at different distances from the axis of rotation in a rotating body.

Application of Moment of Inertia

Moment of Inertia has various applications some of which are discussed below:

• Due to the greater moment of inertia, the earth is rotating on its axis with the same angular velocity.
• A small moving wheel is placed under the children’s play motor. After rubbing this wheel with the ground and leaving the motor, due to the moment of inertia of the wheel, the motor keeps running for some time.
• Each engine consists of a large and heavy wheel attached to its shaft, with most of its mass on its circumference. Therefore, its moment of inertia is high. This wheel is called a flywheel. The torque that drives the shaft of the engine keeps on increasing. Therefore, the rotation of the shaft may not be uniform, but due to the presence of a moving wheel with more inertia, the shaft continues to rotate at an almost uniform speed.
• In the wheel of bullock carts, rickshaws, scooters, cycles, etc., most of the mass is concentrated on its circle or rim. this hoop or routine is attached to the axis of the wheel by rigid spokes. By doing this its moment of inertia increases. Therefore, when the legs stop moving while cycling, the wheel continues to spin for some time.

Solved Examples on Moments of Inertia

Example 1: A body of mass 500 g is rotating about an axis. the distance of the center of mass of the body from the axis of rotation is 1.2 m. find the moment of inertia of the body about the axis of rotation.

Solution:

Given that M = 500 g = 0.5 kg, r = 1.2 m.

Obviously, the entire mass of a body can be assumed to be placed at its center of mass. Then the moment of inertia of the body about the axis of rotation.

I = Mr²

I = 0.5 × (1.2)²

I = 0.72 kg m²

Example 2: The radius of revolution about an axis 12 cm away from the center of mass of a body of mass 1.2 kg is 13 cm. Calculate the radius of revolution and moment of inertia about an axis passing through the center of mass.

Solution: 

Given that, M = 1.0 kg, K = 13 cm, l = 12 cm, K_CM = ?, I_CM = ?

From Theorem of Parallel Axis I = I_CM + Ml²

K² = K_CM2 + l²

or K_CM2 = K² – l²

K_CM2 = (13)² – (12)² = 25

K_CM = 5

Now, Moment of Inertia I_CM = MK_CM2

I_CM = 1.0 × (0.05)² = 2.5 × 10^-3 kg m²

Example 3: A body of mass 0.1 kg is rotating about an axis. if the distance of the center of mass of the body from the axis of rotation is 0.5 m, then find the moment of inertia of the body.

Solution:

Given that, M = 0.1 kg and r = 0.5 m

so I = Mr²

I = 0.1 × (0.5)²

I = 0.025 kg m²

Example 4: The moment of inertia of the rings about an axis passing through its center perpendicular to the plane of the circular ring is 200 gm cm². What will be the moment of inertia about its diameter?

Solution: 

Moment of Inertia of a circular ring about an axis passing through another center perpendicular to its plane

MR² = 200 gm cm²

Moment of inertia about to diameter

= 1/2 MR²

= 1/2 × 200 = 100 gm cm²

FAQs on Moments of Inertia

1. How to calculate the Moment of Inertia?

The basic formula for finding the moment of inertia of any uniform object is,

I = mr²

where,
m is the mass of the object’
r is the distance from the axis of rotation

2. How to calculate the Moment of Inertia of a Beam?

Moment of Inertia of a Beam along the center and axis horizontal to it is calculated using the formula,

I = ML² / 12

3. On what does the Moment of Inertia of a body depend?

The moment of inertia of any object depends on the factors given below:

• Mass of the Body,
• Axis of rotation
• Shape and size of the object

4. What is the Unit of Moment of Inertia?

The unit of Moment of Inertia is Kgm²

5. Can the Moment of Inertia be Negative?

No, the moment of inertia can never be negative.

6. What is Mass Moment of Inertia?

Mass Moment of Inertia is the measurement of a body’s resistance to change in its angular momentum or direction. The Mass Moment of Inertia for a point mass is given by I = mr² and for system of particles, the mass moment of inertia is given as I = Σ_im_ir_i²

7. What is Area Moment of Inertia?

Area Moment of Inertia is property of a 2D shape plane which shows how points are dispersed with respect to an arbitrary axis in a plane. Area Moment of Inertia is also known as Second Moment of Area or Quadratic Moment of Area. The formula for Area Moment of Inertia in xy plane is given as I_xy = ∫xy dxdxy = ∫xy dA