Relation between Angular Velocity and Linear Velocity
Last Updated :
12 Oct, 2021
Motion is described as a change in position over a period of time. In terms of physics and mechanics, this is called velocity. It is defined as the change in position over a period. Rotational Motion is concerned with the bodies which are moving around a fixed axis. These bodies in rotation motion often exhibit behaviors that are similar to the behaviors exhibited by them during translatory motion. For example, angular velocity and velocity in the translatory motion are analogous and so are torque-force and mass-moment of inertia.
Angular Rotation
Rotational motion is the circular motion around a fixed axis. While working on rotational motion problems, we try to draw similarities between translatory and rotational motion and use similar variables. The angle of rotation is defined by the angle covered by the body. It is denoted by the notation theta(). While doing rotational motion, the object does a circular motion. The arc length is the distance traveled by the object in rotational motion. This distance and angular rotation are related by the radius of curvature.

Let the arc length be denoted by “s” and the radius of curvature be denoted by “r”.
θ = s/r

Angular Velocity
Suppose a body is rotating around some fixed axis. Then the body changes its angle with time. Denoting the angle by θ, the angular velocity is defined as the rate of change of the angle of the body. Angular velocity is denoted by ω. If the body is rotating at a constant rate, the average angular velocity is used,
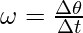
In the cases where the rotational motion is not constant, instantaneous angular velocity is calculated.
ω = dθ/dt

As shown in the figure, the angular velocity is directed towards the fixed axis.
Angular Velocity and Linear Velocity
Linear Velocity is the measure of how much distance an object covers per unit of time. For an object moving in a circular motion, the linear velocity is related to the angular velocity. The object covering an angle is also covering some distance in terms of a circular arc. Let us say that the linear velocity of a particle P rotating around a fixed axis is given by,

It is known that,
s = rθ
Substituting the value of “s” in the equation given above,
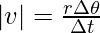
⇒ 
Substituting the values of angular velocity discusses in the previous section.
|v| = rω
Sample Problems
Question 1: Find the angular velocity of the ball traveling at a speed of 10 m/s in a 20m radius circle.
Answer:
The relation between angular and linear velocity of the ball is given by,
|v| = rω
Given:
v = 10 m/s
r = 20m
Find:
ω = ?
v = rω
⇒ 10 = (20)ω
⇒ 0.5 m/s = ω
Question 2: Find the angular velocity of the ball traveling at a speed of 100 m/s in a 5m radius circle.
Answer:
The relation between angular and linear velocity of the ball is given by,
|v| = rω
Given:
v = 100 m/s
r = 5m
Find:
ω = ?
v = rω
⇒ 100 = (5)ω
⇒ 20 m/s = ω
Question 3: Find covers a full circle in 20 seconds. Find the angular velocity of the particle.
Answer:
Angular Velocity is given by,
ω = (Angle Covered)/(Time)
Given:
Angular Covered = 360°
= 2π
Time “t” = 20 seconds.
Find:
ω = (Angle Covered)/(Time)
⇒ ω = 2π / 20
⇒ ω = π /10 rad /s.
Question 4: Find covers 270 degrees in 5 seconds. Find the angular velocity of the particle.
Answer:
Angular Velocity is given by,
ω = (Angle Covered)/(Time)
Given:
Angular Covered = 270°
= 3π/4
Time “t” = 5 seconds.
Find:
ω = (Angle Covered)/(Time)
⇒ ω = 3π / (4)(5)
⇒ ω = 3π /20 rad /s.
⇒ ω = 0.15π rad /s.
Question 5: A planet is moving around its sun in a circular manner. The angular velocity of the planet is 0.5 rad/s. The distance of the planet from its sun is estimated at 1,00,000 Km. Find out the linear velocity of the planet.
Answer:
The relation between angular and linear velocity of the ball is given by,
|v| = rω
Given:
ω = 0.5 rad/s
r = 105 Km
⇒ r = 108 m
Find:
v = ?
v = rω
⇒ v = (108)(0.5)
⇒ 5 × 107 m/s = v
Share your thoughts in the comments
Please Login to comment...