Humans learn early in life that all material items have a natural tendency to gravitate towards the earth. Anything thrown up falls to the ground, traveling uphill is much more exhausting than walking downhill, Rains from the clouds above fall to the ground, and there are several additional examples.
Earth’s satellites are celestial objects that orbit the earth. Their movement is similar to that of the planets’ orbits around the Sun, and hence The rules of planetary motion established by Kepler are equally valid and are applicable to them. Earth’s satellite orbits around the earth are circular or elliptic. The moon is the Earth’s only natural satellite. Many countries, including India, have been able to launch artificial earth satellites for use in areas such as telecommunications, geophysics, and meteorology because of technological advancements.
What is Gravitation?
Gravitation, or simply gravity, is the force that attracts two bodies together. All objects in the cosmos attract each other with a certain level of force, but due to the vast distances between the objects, the force is too faint to be noticed in most circumstances. Furthermore, while gravity’s range is infinite, the effect weakens as objects travel more away.
Gravitation potential energy: The energy stored in the body at a certain posture is known as potential energy. If a particle’s location changes as a result of forces operating on it, the change in its potential energy is equal to the amount of work the force does on the body. The gravitational potential energy is the potential energy of a body that arises from the force of gravity. The expression for the potential energy between satellite and the earth can be given as,
P.E = -GMm / r
Binding energy of Satellites or Energy of Orbiting Satellites
Binding Energy is the minimal amount of energy that must be delivered to the satellite in order to free of the planet’s gravitational attraction or the gravitational influence of the planet.
The term “binding energy” refers to the energy that binds the satellite to the Earth. The gravitational attraction between the satellite and the planet will be overcome by this binding energy.
Consider a satellite revolving in a circular path around the earth. The force of gravitational attraction between the earth and the satellite provides the necessary centripetal force to keep the satellite revolving in a stable circular orbit. There are two types of mechanical energies in the satellite as it orbits the planet. Due to its orbiting motion, the kinetic energy exists and due to its position in the gravitational field of the earth’s potential exists energy.
Derivation for the Binding Energy of the Satellites

A satellite above the surface of the earth.
Let, the mass of the earth is M, the mass of the satellite is m, the radius of the earth is R, the height of the satellite from the earth surface is h, the radius of the circular orbit of the satellite is r or (R+h), and the critical velocity of the satellite is v.
A centripetal force equal to gravitational force because it provides the necessary centripetal force which is required for the circular motion i.e.
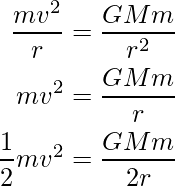
where G is the Universal gravitational constant.
So, the kinetic energy can be written as,
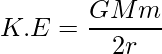
Now, the potential energy between satellite and the earth can be given as,
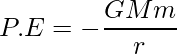
Here the negative sign represents the force that acts between the satellite and earth is attractive. . However, the magnitude of the K.E is half the P.E, so that the total E will be the sum of kinetic energy and potential energy.
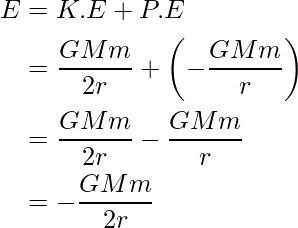
The above expression is the binding energy of the satellite revolving around the earth in a stable circular orbit.
Expression for the Binding Energy of the Satellite stationary on the earth’s surface.
Let, the mass of the stationary satellite is m, therefore the kinetic energy is equal to zero.
Now, the potential energy can be expressed as,
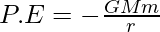
The total E will be the sum of kinetic energy and potential energy,
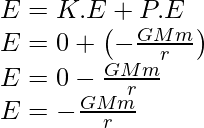
Here the negative sign represents the force that acts between the satellite and earth is attractive.
Earth Satellites
Earth satellites are celestial bodies that orbit the earth. The motion of the celestial bodies is much like the motion of planets that orbit the Sun and hence Kepler’s laws of planetary motion apply to them as well. In general earth’s satellite orbits are circular or elliptic. The moon is the earth’s only natural satellite with a nearly circular orbit and a time period of around 27.3 days, which is almost equivalent to the moon’s rotating period around its own axis.
Let a satellite in a circular orbit of a distance (RE + h) from the center of the earth, where RE is the radius of the earth. If m is the mass of the satellite then the speed of the satellite is given by
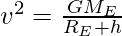
In every orbit, the satellite traverses a distance 2π(RE+ h) with speed V. Its time period T is given by
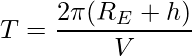
Substitute the value of V in the above expression,
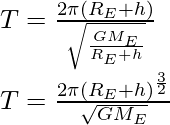
Weightlessness
The force with which the earth attracts an object is called its weight. When we stand on a surface, we are aware of our own weight because the surface exerts an opposing force to keep us at rest. When we use a spring balance suspended from a fixed position, such as the ceiling, to determine the weight of an object, the same principle applies. Unless it is subjected to a force that opposes gravity, the object will fall. The spring puts exactly this force on the object. This is because the object’s gravitational pull pulls the spring down a little, and the spring then exerts a force vertically upwards on the object.
Imagine that the top end of the balance is no longer attached to the room’s top ceiling. The object, as well as both ends of the spring, move at the same g acceleration. The spring is not extended, and it does not exert any upward force on the object, which is falling at g due to gravity. Because the spring is not extended at all, the reading in the spring balance is zero. Because there is no upward force on the object, if it were a human being, he or she would not feel his weight. As a result, when an object is in free fall, it is weightless, and this phenomenon is known as weightlessness.

Every portion and parcel of a satellite orbiting the earth has an acceleration towards the center of the earth equal to the value of the earth’s acceleration owing to gravity at that location. As a result, everything inside the satellite is in free fall. It’s as though a human falling from a great height towards the ground. As a result, humans within a satellite have no sense of gravity. Because gravity defines the vertical direction for humans, they have no horizontal or vertical directions; all directions are the same for them. This is demonstrated by images of astronauts floating in space in a satellite.
Sample questions
Problem 1: A 400 kg satellite is in a circular orbit of radius 2RE about the Earth. How much energy is required to transfer it to a circular orbit of radius 4RE ? What are the changes in the kinetic and potential energies?
Solution:
Given,
The mass of the satellite is 400 kg.
The initial radius of the orbit is 2RE.
The final radius of the orbit is 4RE.
The expression for the binding energy is,
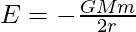 ,
,
So, the binding energy of the satellite at a radius of orbit 2RE is
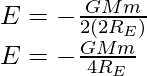
so, the binding energy of the satellite at a radius of orbit 4RE is
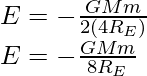
The change in the total energy binding energy is
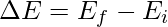
Substitute the initial and final energy in the above expression,
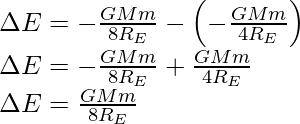
Rearrange the expression and substitute all the values,
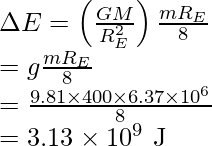
The kinetic energy is reduced and equal to minus of ∆E,
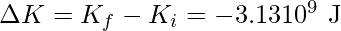
And the change in potential energy is twice the change in the binding energy,
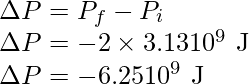
Problem 2: Define binding Energy of the satellite and derive its expression.
Solution:
Binding Energy is the minimal amount of energy that must be delivered to the satellite in order to free of the planet’s gravitational attraction or the gravitational influence of the planet. The term “binding energy” refers to the energy that binds the satellite to the Earth. This energy will overcome the gravitational force of attraction between the satellite and the Earth.
Let, the mass of the earth is M, the mass of the satellite is m, the radius of the earth is R, the height of the satellite from the earth surface is h, the radius of the circular orbit of the satellite is r or (R+h), and the critical velocity of the satellite is v.
The gravitational force provides the necessary centripetal force required for the circular motion. So, a centripetal force equal to gravitational force i.e.
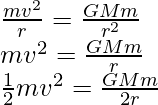
where G is the Universal gravitational constant.
So, the kinetic energy can be written as,
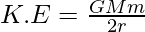
Now, the potential energy between satellite and the earth can be given as,
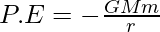
Here the negative sign represents the force that acts between the satellite and earth is attractive. . However, the magnitude of the K.E is half the P.E, so that the total E will be the sum of kinetic energy and potential energy.
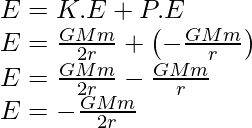
The above expression is the binding energy of the satellite revolving around the earth in a stable circular orbit.
Problem 3: What Is Newton’s Law Of Universal Gravitation?
Solution:
Every particle in the universe attracts all other particles with a force that is proportional to the product of their masses and inversely proportional to the square of their distance.
According to the law a force acting along the line connecting the two points attracts every other point mass, . The force is proportional to the product of the two masses, and it is inversely proportional to the square of their distance.
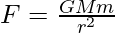
where F is the gravitational force acting between two objects, M and m are the masses of the objects, r is the distance between the centers of their masses, and G is the gravitational constant.
Problem 4: State Kepler’s laws of planetary motion.
Solution:
Kepler’s laws of planetary motion state that:
- The Sun is at one of the elliptical orbits’ focal points, which all planets follow.
- The radius vector drawn from the Sun to a planet covers the same area in the same amount of time. Because of this the gravitational force of the planet is central, so angular momentum is conserved.
- The square of a planet’s orbital period is proportional to the cube of the semimajor axis of the planet’s elliptical orbit. The period T and radius R of a planet’s circular orbit around the Sun are related by
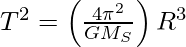
where Ms is the mass of the Sun. Most planets have nearly circular orbits about the Sun. For elliptical orbits, the above equation is valid if R is replaced by the semi-major axis, a.
Problem 5: The planet Mars has two moons, Phobos and Delmos. Phobos has a period of 7 hours, 39 minutes, and an orbital radius of 9.4 ×103 km. Calculate the mass of Mars.
Solution:
Given,
Time is equal to 7 hours, 39 minutes i.e. 459 min and this is equal to (459×60) sec.
An orbital radius is 9.4 ×103 km i.e. 9.4 ×106 m.
According to Kepler’s laws
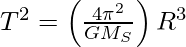
Rearrange the above expression,
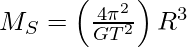
Substitute the values in the above expression,
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...