Kinematics of Rotational Motion
Last Updated :
14 Jul, 2021
It is not difficult to notice the analogous nature of rotational motion and kinematic motion. The terms of angular velocity and angular acceleration remind us of linear velocity and acceleration. So, similar to the kinematic equation of motion. Equations of rotational motion can also be defined. Such equations help us in calculating the parameters such as angle of rotation, angular velocity. Let’s look at these equations and see how they can be used in a similar context.
Kinematics Of Rotational Motion
Rotational quantities such as angle θ, angular velocity ω, and angular acceleration α. Let’s see how the equation of motion relates to the equations of rotational motion. Consider a wheel that starts spinning with angular acceleration and covers many revolutions. In terms of the formal notation, it can be said that a wheel having a large α ends up rotating at a large angle through a number of revolutions (θ). This situation is similar to a vehicle moving on a road with some acceleration and attaining some velocity. These parameters can be calculated using the kinematics of linear motion. A similar approach can be used in rotational motion. These equations are called kinematic equations of rotational motion. The table below represents some analogous quantities.
| Rotational | Translational |
| ω | v |
| θ | s |
| α | a |
| θ = ωt | s = vt |
Kinematic Equations of Motion
For an object moving with an acceleration “a”. Let’s say the time is denoted by “t”, present velocity by “v”, initial velocity by “u” and the distance covered by the object by “s”. The equations governing this motion are given below. Keep in mind that these equations are only for situations where acceleration “a” is constant and the object is moving in a straight line.
- v = u + at
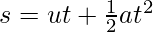
- v2 = u2 + 2as
Now, in the case of rotational motion, velocity(v) corresponds to the angular velocity(ω). Displacement “s” is analogous to angle of rotation(θ), acceleration(a) is analogous to angular acceleration(α).
Kinematic Equations for Rotational Motion
For an object rotating with an angular acceleration α. Let’s say the time is denoted by “t”, present angular velocity by ω, initial velocity by, and the angle covered by the object by θ. The equations governing this motion are given below. Keep in mind that these equations are only for situations where angular acceleration is constant.
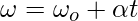
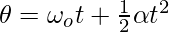
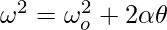
Sample Questions
Question 1: If a body is rotating at an angular velocity of 15rad/s, what would be the angular displacement in 5 seconds?
Answer:
Let 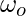 denote the initial angular velocity.
denote the initial angular velocity.
Given: 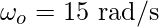
The goal is to find angular displacement 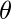
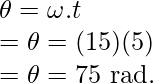
Question 2: If a body is rotating with an acceleration of 2 radians/s2. If the initial angular velocity was 15rad/s, what would be the speed in 5 seconds?
Answer:
Let 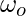 denote the initial angular velocity and
denote the initial angular velocity and 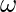 denote the final angular velocity.
denote the final angular velocity.
Given: 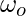 = 15,
= 15, 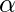 = 2 radians/s2
= 2 radians/s2
For finding out the value of “v”, the first equation of motion can be used.
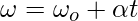
Plugging the values in this equation,
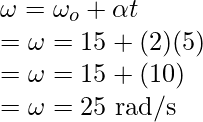
Question 3: If a body is rotating with an acceleration of -10 radians/s2. If the initial angular velocity was 30rad/s, what would be the speed in 5 seconds?
Answer:
Let 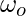 denote the initial angular velocity and
denote the initial angular velocity and 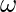 denote the final angular velocity.
denote the final angular velocity.
Given: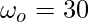 ,
, 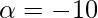 radians/s2
radians/s2
For finding out the value of “v”, the first equation of motion can be used.
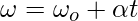
Plugging the values into this equation,
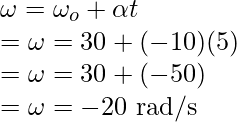
Question 4: If a body is moving at an angular acceleration of 5 rad/s2. If the initial speed was 40rad/s, what would be the angle covered in 3 seconds?
Answer:
Let u denote the initial velocity
Given: 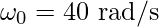 ,
, 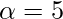 and t = 5
and t = 5
For finding out the value of “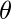 “, the first equation of motion can be used.
“, the first equation of motion can be used.
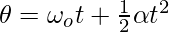
Plugging the values into this equation,
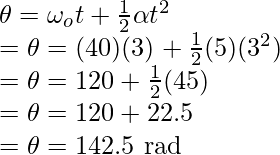
Question 5: If a body is moving at an angular acceleration of 2 rad/s2. If the initial speed was 10rad/s, what would be the angle covered in 10 seconds?
Answer:
Let u denote the initial velocity
Given: 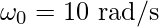 ,
, 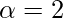 and t = 5
and t = 5
For finding out the value of “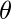 “, the first equation of motion can be used.
“, the first equation of motion can be used.
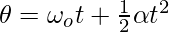
Plugging the values into this equation,
Question 6: The wheel of a racing car catches a speed of 20rad/s in 2 seconds. Find the angular displacement of the car wheel in the process.
Answer:
Let  denote the initial angular velocity and
denote the initial angular velocity and  denote the final angular velocity.
denote the final angular velocity.
Given: 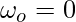 ,
, 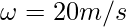 and t= 2.
and t= 2.
For finding out the value of “a”, the first equation of motion can be used.
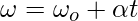
Plugging the values in this equation,
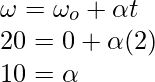
For finding out the distance, a third equation of motion will be used.
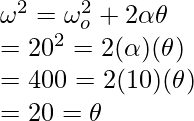
Question 7: The wheel of a racing car catches a speed of 40rad/s in 4 seconds. Find the angular displacement of the car wheel in the process.
Answer:
Let 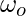 denote the initial angular velocity and
denote the initial angular velocity and 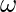 denote the final angular velocity.
denote the final angular velocity.
Given: 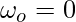 ,
,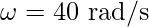 and t = 4.
and t = 4.
For finding out the value of “a”, the first equation of motion can be used.
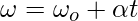
Plugging the values into this equation,
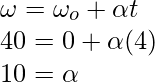
For finding out the distance, a third equation of motion will be used.
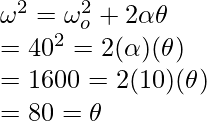
Share your thoughts in the comments
Please Login to comment...