Problems on Friction Formula
Last Updated :
14 Jul, 2021
Friction is a force that is present almost everywhere in daily life. This force allows us to walk, hold objects, etc. In short, it is essential for almost all physical actions in real life. When a ball is thrown on the floor with some velocity, it keeps moving for some time and then comes to a halt. In an ideal scenario, the ball should keep moving as there is no external force acting on the ball. But it comes to rest, which means that there is a force present that resists the motion. This force is called friction. Frictional force by nature opposes all sorts of motion between objects.
Friction
Frictional forces oppose the motion. While it usually generates heat and wears and tear objects, it is often helpful. It gives the necessary traction needed for walking and running without slipping. In automobiles, it is less desired as it accounts for 20% of energy loss. Friction depends upon the normal force acting on the surface. Frictional forces can be divided into two parts:
- Static Friction: This is a type of friction that prevents objects from sliding on a surface. The direction stops the objects from sliding against one another and is parallel to the surface.
- Kinetic Friction: This type of friction acts when an object slides on the surface. The direction is the same as static friction.
Laws of Friction:
- Friction of the moving object is proportional and perpendicular to the normal force applied on it.
- The friction experienced by the object depends on the nature of the surface it is in contact with.
- Friction is independent of the area of contact as long as there is an area of contact.
- Kinetic friction is independent of velocity.
- The coefficient of static friction is greater than the coefficient of kinetic friction.
Equations of Friction
When a force is applied to the object, let’s say FN is the force acting normally on the surface. The value of the static friction is given by Fs and 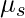 is the value of the coefficient of static friction. Then the equation governing the static force of friction is given by,
is the value of the coefficient of static friction. Then the equation governing the static force of friction is given by,

In the case where the object is moving, the kinetic force of the friction will be given by,

The coefficient of friction is given by,
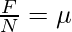
Here, F is the force of friction and N is the value of the normal force.
Let’s look at some problems related to these concepts.
Sample Problems
Question 1: Force of 60N is exerted on the box kept on the floor with the coefficient of static friction of 0.4. Find the friction force.
Answer:
Force of static friction is given by,
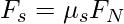
Here, 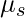 is the coefficient of static friction and N is the normal force.
is the coefficient of static friction and N is the normal force.
 and N = 60N
and N = 60N
Plugging the values in the equation,
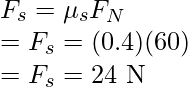
Question 2: Force of 100N is exerted on the box kept on the floor with the coefficient of static friction of 0.2. Find the friction force
Answer:
Force of static friction is given by,
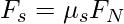
Here, 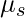 is the coefficient of static friction and N is the normal force.
is the coefficient of static friction and N is the normal force.
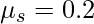 and N = 100N
and N = 100N
Plugging the values in the equation,
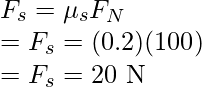
Question 3: Force of 100N is exerted at an angle of 30° on the box kept on the floor with the coefficient of static friction of 0.2. Find the friction force

Answer:
Force of static friction is given by,
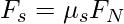
Here, 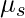 is the coefficient of static friction and N is the normal force.
is the coefficient of static friction and N is the normal force.
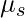 = 0.2,
= 0.2, 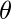 = 30° and F = 100N
= 30° and F = 100N
N = Fsin(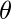 )
)
⇒N = (100)sin(30°)
⇒N = 50
Plugging the values in the equation,
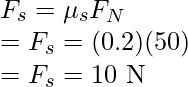
Question 4: Force of 200N is exerted at an angle of 30° on the box kept on the floor with the coefficient of static friction of 0.2. Find the friction force

Answer:
Force of static friction is given by,
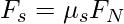
Here, 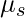 is the coefficient of static friction and N is the normal force.
is the coefficient of static friction and N is the normal force.
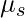 = 0.2,
= 0.2, 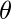 = 30° and F = 200N
= 30° and F = 200N
N = Fsin(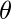 )
)
⇒N = (200)sin(30°)
⇒N = 100
Plugging the values in the equation,
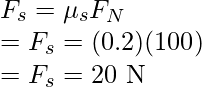
Question 5: Force of 60N is exerted horizontally on the box of 40Kg kept on the floor with the coefficient of static friction of 0.2. Find the friction force.
Answer:
Force of static friction is given by,
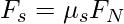
Here, 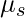 is the coefficient of static friction and N is the normal force.
is the coefficient of static friction and N is the normal force.
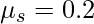 and N = mg
and N = mg
N = mg
⇒N = (40)(10)
⇒N = 400N
Static friction will be,
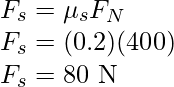
Now, the applied force is 60N and the maximum static friction is 80N. Since the applied force is less than the value of static friction, the box will not move and the frictional force will be equal to the applied force.
Question 6: Force of 50N is exerted horizontally on the box of 50Kg kept on the floor with the coefficient of static friction of 0.3. Find the friction force.
Answer:
Force of static friction is given by,
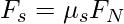
Here, 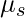 is the coefficient of static friction and N is the normal force.
is the coefficient of static friction and N is the normal force.
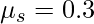 and N = mg
and N = mg
N = mg
⇒N = (50)(10)
⇒N = 500N
Static friction will be,

Now, the applied force is 100N and the maximum static friction is 150N. Since the applied force is less than the value of static friction, the box will not move and the frictional force will be equal to the applied force.
Question 7:A horizontal force of 40N is exerted on a box of 2Kg kept on the floor with the coefficient of static friction of 0.4 and a coefficient of kinetic friction is 0.2. Find the force of friction.
Answer:
Force of static friction is given by,
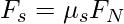
Here, 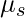 is the coefficient of static friction and N is the normal force.
is the coefficient of static friction and N is the normal force.
 and N = mg
and N = mg
N = mg
⇒N = (2)(10)
⇒N = 20N
Plugging the values in the equation,
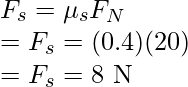
Now, since the maximum static friction is less than the force applied. The box will start moving and then the kinetic friction will act on the body.
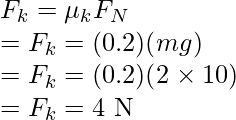
Question 8:A horizontal force of 50N is exerted on a box of 3Kg kept on the floor with the coefficient of static friction of 0.4 and a coefficient of kinetic friction is 0.2. Find the force of friction.
Answer:
Force of static friction is given by,
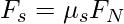
Here, 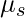 is the coefficient of static friction and N is the normal force.
is the coefficient of static friction and N is the normal force.
 and N = mg
and N = mg
N = mg
⇒N = (3)(10)
⇒N = 30N
Plugging the values in the equation,
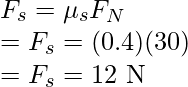
Now, since the maximum static friction is less than the force applied. The box will start moving and then the kinetic friction will act on the body.
Share your thoughts in the comments
Please Login to comment...