Pascal’s law establishes the relation between pressure and the height of static fluids. A static fluid is defined as a fluid that is not in motion. When the fluid is not flowing, it is said to be in hydrostatic equilibrium. For a fluid to be in hydrostatic equilibrium, the net force on the fluid must be zero. This law can be applied to a wide range of real-life applications and hydraulic machines are one of the widely used applications of this law. These hydraulic systems allow us to design shockers and heavy-lifting machines.
What is Pascal’s Law?
Pressure is defined as the ratio of the force applied and the cross-sectional area. In 1653, Blaise Pascal published his book The Physical Treatises of Pascal in which he discussed the principles of static fluids. He observed that pressure in a fluid at rest is the same at all points if these points are at the same depth and if we apply external pressure to this fluid, all the applied force is distributed throughout the liquid.
In other words, all the externally applied static pressure on a confined liquid is equally transmitted throughout the liquid in all directions.
Pascal’s Law Formula
Pressure is defined as the ratio of the Force and cross-sectional area on which that force is applied, mathematically we can represent the same as follows:
P = F/A
Where,
- P is pressure,
- F is applied force,
- and A is the cross-sectional area.
Difference of Pressure in Column
The figure shows a cylindrical element submerged in the fluid of density ρ, of area A and height h. Let the pressure at the top of the element be P1 and P2 at the bottom. Let us assume that the weight of the liquid is “mg” in this element. Then the difference in pressures between the two points is given by,
P1 – P2 = mg/A
Now, as the density of the liquid is “ρ”, then the mass of the liquid in the element will be,
m = ρ(A.h)
or
m = ρ.A.h
Plugging this value of m in the above equation for the pressure difference,
P1 – P2 = ρgh
This extra pressure with the height “h” is called gauge pressure.
Pascal’s Law Definition
Pascal’s law states that whenever external pressure is applied to any part of a liquid. This pressure gets distributed in all directions equally. A number of devices are based on this principle. The hydraulic lift is also an application of this law.
This law helps us design hydraulic machines which are very useful in industries. Consider a hydraulic lift as given in the figure below. The two pistons are separated by a space filled with liquid. A piston of small cross-section A1 is used to exert a force F1 directly on the liquid. F2 denotes the force that is felt on the second piston due to the force applied on the piston with cross-section A1.
The pressure that is exerted in the column is given by, P = F1/A1. This is transmitted throughout the liquid, which results in the pressure being applied on the other piston. The area of the other piston is A2, the force felt by this piston is given by,
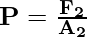
Now, as pressure throughout the liquid remains the same
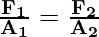
Or
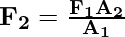
This tells us that the applied force is increased by the factor of A2/A1. This property helps in hydraulic systems for lifting very heavyweights.
Pascal’s Law Derivation
Let us consider a right-angled triangle(with sides p, q, and r) prism (height s) submerged in the liquid of density ρ, also assume the size of the submersed element is negligible with compare to the volume of the liquid, and all the points on the element experience the same gravitational force.
Now, the area of the faces PQRS, PSUT, and QRUT of the prism is ps, qs, and rs respectively. Also, assume the pressure applied by the liquid on these faces is P1, P2, and P3 respectively.
Exerted force by this pressure to the faces in the perpendicular inward direction is F1, F2, and F3.
Thus, F1 = P1 × Area of PQRS = P1 × ps
F2 = P2 × Area of PSUT = P2 × qs
F3 = P3 × Area of QRUT = P3 × rs
Now, in triangle PQT,
sin θ = p/r and cos θ = q/r
The net force on the prism will be zero since the prism is in equilibrium.
F3 sin θ = F1 and F3 cos θ = F2 (putting values of F1, F2, and F3 from the above values)
⇒ P3 × rs × p/r = P1 × ps and P3 × rs × q/r = P2 × qs
⇒ P3 = P1 and P3 = P2
Thus, P1 = P2 = P3
Therefore, pressure throughout the liquid remains the same.
Applications of Pascal’s Law
The application of Pascal’s Law can be seen throughout industries. Some of the applications are as follows:
- Hydraulic Lift
- Hydraulic Jack
Now let’s learn about them in detail.
Hydraulic Lift
By applying Pascal’s Law of transmission in real life, we can use it to lift heavy equipment such as cars, trucks, cargo containers, etc. As the ratio of force and the cross-sectional area remains constant throughout the liquid, applying a small force to the small cross-sectional area can exert higher force at a high cross-sectional area, so that ratio remains the same. The image added below shows a hydraulic lift lifting a vehicle.
Hydraulic Jack
Hydraulic Jacki is the less powerful version of the Hydraulic lift which can help us lift our cars or heavy motor vehicles partially for maintenance and other purposes. It uses the same principle but on a small scale. The hydraulic jack is shown in the image below.
Other than the above-mentioned use cases Hydraulic Braking Systems and Hydraulic Pumps also leverages the same principles to stop cars/heavy motor vehicles and pump water respectively.
Sample Problems on Pascal’s Law
Problem 1: Find the pressure difference that comes when someone goes 8m deep inside the water. Given, the density of water = 900Kg/m3.
Answer:
The difference between the pressures is given by,
P1 – P2 = dgh
Given: d = 900, g = 10 and h = 8
P1 – P2 = dgh
⇒P1 – P2 = (900)(10)(8)
⇒P1 – P2 = 72 × 103 Kg/m2
Problem 2: Find the pressure difference that comes when someone goes 5 m deep inside a liquid. Given the density of liquid = 100Kg/m3.
Answer:
The difference between the pressures is given by,
P1 – P2 = dgh
Given: d = 100, g = 10 and h = 5
P1 – P2 = dgh
⇒ P1 – P2 = (100)(10)(5)
⇒ P1 – P2 = 5 x 103 Kg/m2
Problem 3: A hydraulic system has pistons at its two ends. The area of the pistons is given by A1 = 1m2 and A2 = 0.2m2. A Force of 80N is applied on the piston with a smaller area. Find the force on the other end.
Answer:
In a hydraulic system, the force on the other end is given by,
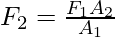
Given: A1 = 1m2 and A2 = 0.2m2. F1 = 80N
Plugging the values in the equation,
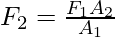
⇒ 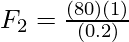
⇒ F2 = 400N
Problem 4: A hydraulic system has circular pistons at the two ends. The radius of these pistons is 30cm and 60cm. A 50 kg box is kept on the piston with a 40cm radius, find the force that should be applied at the other end.
Answer:
In a hydraulic system, the force on the other end is given by,
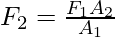
Given: A1 = 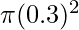 m2 and A2 =
m2 and A2 = 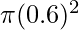 m2. F2 = 500N
m2. F2 = 500N
Plugging the values into the equation,
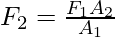
⇒ 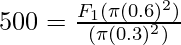
⇒ 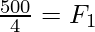
⇒ F1 = 125N
Problem 5: In a car wash, the hydraulic system has pistons at its two ends. The area of the pistons is given by A1 = 0.5m2 and A2 = 4m2. A Force of 80N is applied to the piston with a smaller area. Find the force on the other end.
Answer:
In a hydraulic system, the force on the other end is given by,
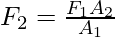
Given: A1 = 0.5m2 and A2 = 4m2. F1 = 80N
Plugging the values into the equation,
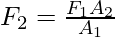
⇒ 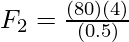
⇒ F2 = 640 N
Problem 6: A hydraulic piston has two ends of the area A1 = 0.4m2 and A2 = 0.1m2. The goal is to pick the 50 kg box kept on the piston with a 0.4 m2 area, find the force that should be applied at the other end.
Answer:
In a hydraulic system, the force on the other end is given by,
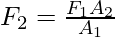
Given: A1 = 0.1m2 and A2 = 0.5m2. F2 = 500N
Plugging the values into the equation,
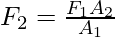
⇒ 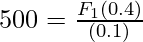
⇒ F1 = 125 N
Problem 7: A hydraulic piston has two ends of the area A1 = 0.4m2 and A2 = 0.1m2. The goal is to pick the 50Kg box kept on the piston with 0.4 m2 area. , find the force that should be applied at the other end.
Answer:
In a hydraulic system, the force on the other end is given by,
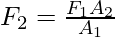
Given: A1 = 0.1m2 and A2 = 0.5m2. F2 = 500N
Plugging the values into the equation,
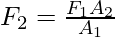
⇒ 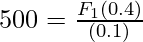
⇒ F1 = 125 N
Problem 8: A hydraulic system has circular pistons at the two ends. The radius of these pistons is 20cm and 40cm. A 100Kg box kept on the piston with a 40cm radius, find the force that should be applied at the other end.
Answer:
In a hydraulic system, the force on the other end is given by,
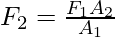
Given:
A1 = 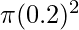 m2 and A2 =
m2 and A2 = 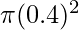 m2. F2 = 1000N
m2. F2 = 1000N
Plugging the values into the equation,
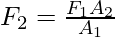
⇒ 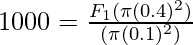
⇒ 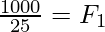
⇒ F1 = 40N
FAQs on Pascal’s Law
Q1: State Pascal’s Law.
Answer:
Pascal’s Law states that the externally applied static pressure on a confined liquid is equally distributed throughout the liquid in all directions.
Q2: Who stated Pascal’s Law?
Answer:
Blaise Pascal gave Pascal’s Law in 1653, he was a French mathematician cum philosopher.
Q3: What are the Applications of Pascal’s law?
Answer:
Applications of Pascal’s Law are Hydraulic lift, Hydraulic jack, Hydraulic pump and also Hydraulic Breaking System etc.
Q4: Is Pascal’s Law applicable to gas?
Answer:
Yes, Pascal’s Law is applicable to gas. It states that in a closed container, the pressure applied to one part of the container is transmitted to all parts equally.
Q5: How much is 1 Pascal?
Answer:
One Pascal in SI units is expressed as,
1 Pa = 1 N/m2
Q6: State Pascal’s Law of Transmission of Pressure.
Answer:
Pascal’s Law of Transmission states that whenever external pressure is applied to any part of a liquid. This pressure gets distributed in all directions equally.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...