Motion of a Rigid Body
Last Updated :
06 Oct, 2021
A rigid body is a solid body that has little to no deformation when a force is applied. When forces are applied to such bodies, they come to translational and rotational motion. These forces change the momentum of the system. Rigid bodies are found almost everywhere in real life, all the objects found in real life are rigid in nature. It becomes essential to study the motion and the effects different forces have on them to be able to predict their trajectories. These kinds of predictions are used while making video games, robots, and spacecraft. Let’s see these concepts in detail.
Rigid Body Dynamics
The concepts for rigid body dynamics were developed when classical mechanics was not able to solve motion and kinematic problems for bodies that did not point masses and were susceptible to rotation when forces were applied to them. A rigid body can have two types of motions when forces are applied to it:
- Translatory Motion.
- Rotational Motion.
Translational Motion
A body is said to be in translatory motion when all the particles on that body are moving the same distance in equal time intervals. This motion can be rectilinear or curvilinear. Some examples of translational motion include – a car moving in a straight line, a box sliding down a wedge. This kind of motion of governed by the equations of motion and Newton’s laws.
Let F1, F2, F3, … Fn be the vector forces that are acting on the body. These forces cause acceleration in the direction where their resultant lies. This motion is governed by Newton’s Law.
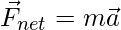
⇒ 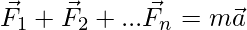
Where “m” is the mass of the system and a is the resultant acceleration of the body.
Rotational Motion
A body is said to be in rotational motion when all the particles constituting the body are moving around a common rotational axis in the same direction. It is a type of circular motion. The examples for rotational motions include – tires of a car moving on the road, a ball rolling down a wedge, etc. Similar to translational motion, this motion can also be described by extending the laws and equations used in translation motion.
Let 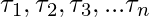 be the torques that are acting on the body. These torques cause angular acceleration in the direction where their resultant lies.
be the torques that are acting on the body. These torques cause angular acceleration in the direction where their resultant lies.
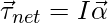
⇒ 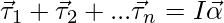
Where “I” is the moment of inertia of the system and α is the resultant acceleration of the body.
Conditions for Equilibrium
A rigid body is said to be in mechanical equilibrium if neither the angular momentum nor the linear momentum of the body is changing with time. This means that it is a condition when the body neither has linear acceleration nor angular acceleration. Let us consider a body of mass “m” and a moment of inertia “I”. Assume that a number of forces are acting on the body which also produces a torque on the body in different directions. If the body is in mechanical equilibrium, it will follow the above-mentioned conditions:

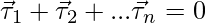
Sample Problems
Question 1: Find the torque of the force on a rigid body whose center of mass is located at the origin. The force is 5i + j + k while the position vector is given by i + k.
Answer:
Torque is given by,
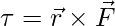
Given:
r = i + k
F = 5i + j + k
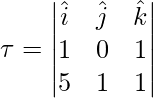
⇒ 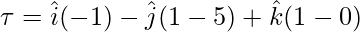
⇒ 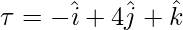
Question 2: Find the torque of the force on a rigid body whose center of mass is located at the origin. The force is i + j + k while the position vector is given by: k.
Answer:
Torque is given by,
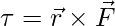
Given:
r = k
F = i + j + k
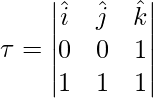
⇒ 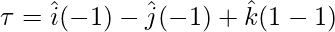
⇒ 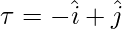
Question 3: Position vector and linear momentum of a body is given by r = 3i + 4j + k m and p = 5j Kg/s. Find the angular momentum.
Answer:
Angular Momentum is given by,
l = r × p
Given: r = 3i + 4j + k, p = 5j.

Question 4: Position vector and linear momentum of a body is given by r = i + j + k m and p = i + j Kg/s. Find the angular momentum.
Answer:
Angular Momentum is given by,
l = r × p
Given: r = i + j + k, p = i + j.
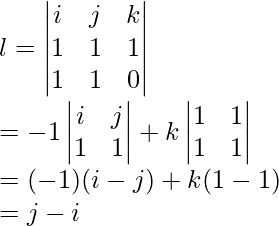
Question 5: A body is revolving around an axis in a circular motion with a radius of 0.1m, the momentum of the body is given by 50 Kgm/s. A torque is applied on the body for 4 seconds and the momentum becomes 100Kgm/s. Find the torque applied to the body.
Answer:
Angular momentum of a body is given by,
l = r × p
Where r is the perpendicular distance of the force from the rotational axis and p is the linear momentum.
Rate of Change in angular momentum gives us the torque.
Initial angular momentum
li = 0.1 × 50
li = 5
Final angular momentum
li = 0.1 × 100
li = 10
Rate of change of angular momentum = 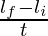
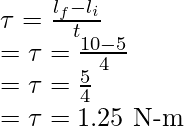
Question 6: A body is revolving around an axis in a circular motion with a radius of 0.2m, the momentum of the body is given by 70 Kg/s. A torque is applied on the body for 2 seconds and the momentum becomes 120Kgm/s. Find the torque applied to the body.
Answer:
Angular momentum of a body is given by,
l = r × p
Where r is the perpendicular distance of the force from the rotational axis and p is the linear momentum.
Rate of Change in angular momentum gives us the torque.
Initial angular momentum
li = 0.2 × 70
li = 14
Final angular momentum
li = 0.2 × 120
li = 24
Rate of change of angular momentum = 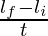
Share your thoughts in the comments
Please Login to comment...