A particle moving in a 1-dimensional space requires only one coordinate to specify its position. In two dimensions similarly, two coordinates are required. Three-dimensional motions are encountered at a lot of places in real life, to analyze these real-life situations. One needs to understand the motion and how to deal with these three coordinates mathematically to describe the trajectories of objects traveling in a three-dimensional plane. Let’s look at these concepts in detail.
Motion in a Three-Dimensional Space
Suppose a particle is moving between two points in a three-dimensional space. To describe the position of this particle, a position vector is required. These vectors are always with respect to the reference frame at the origin. The following parameters are required to fully describe the behavior of a particle moving in a plane,
- Position
- Velocity
- Acceleration
Position Vector
In a 3-d space, a particle can be anywhere, it cannot be described by just one coordinate. In this case, it is denoted with respect to the origin and it also constitutes the direction one should go in to find that point. That is why a vector is required to describe the position. The vector which denotes the position and direction of the particle’s position with respect to the origin is called the position vector. The position vector 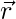 for a particle is given by,
for a particle is given by,
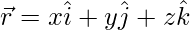
Where x, y, and z are their components along the x, y, and z-axis.

Velocity
The velocity of a particle traveling in the three-dimensional space can be described in two ways – average velocity and instantaneous velocity. When the particle is under acceleration, it changes its velocity every second. So, a single value cannot be assigned to a velocity. In such cases, the instantaneous velocity is preferred, it describes the velocity and its direction at a particular instant. It is given by,
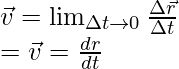
Velocity can also be expressed as,
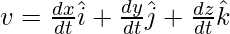
The average velocity is the ratio of total displacement over total time. Suppose a particle goes from 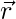 to
to 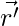 in a total time of
in a total time of 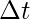
The velocity is given by,
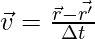
Acceleration
The acceleration of a body moving in a plane is given by the rate of change in its velocity. Similar to velocity, there can be two cases here too – average acceleration and instantaneous acceleration. Average acceleration is given by the ratio of the net change in the velocity of the object with the total time taken. Let initial and final velocities be denoted by 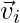 and
and 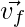
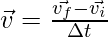
Instantaneous acceleration is used when the acceleration of the body is changing with time.
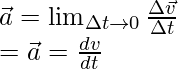
Decomposing this into its components,
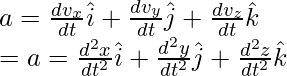
The magnitude of acceleration can also be calculated using the components of velocity,
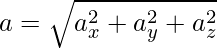
Relative Motion in Three Dimensions
Relative motion represents the velocity of some body as seen from one frame of reference. These concepts have been known in form of one-dimensional and second-dimensional spaces. But these concepts can be extended to three-dimensional spaces also. Given in the figure below, consider a particle P and reference frames S and S’. The position of the frame S’ as measured in S is rS’S, the position of the particle P as measured with respect to the frame S’ is given by rPS’ and the position of the particle P with respect to the frame of reference S is given by rPS,

Notice from the figure that,
rPS = rPS’ + rS’S
These vectors give us the formula for relative velocities too, differentiating the above equation,
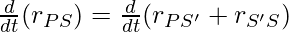
⇒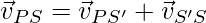
Intuitively speaking, the velocity of a particle with respect to S is equal to the velocity of S’ with respect to S plus the velocity of the particle with respect to S. Differentiating this equation again, the equation for the acceleration is given by,
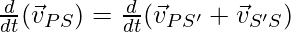
⇒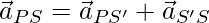
The acceleration of a particle with respect to S is equal to the acceleration of S’ with respect to S plus the acceleration of the particle with respect to S.
Sample Problems
Question 1: Find the velocity at t = 2, for the particle which is moving in a plane and whose position is given, r = t2i + t2j + tk
Answer:
Given: the initial and final position vectors,
r = t2i + t2j + tk
The velocity in this case is given by the formula,
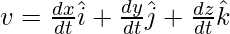
Here x(t) = t2 and y(t) = t2 and z(t) = t
Plugging these values into the equation,
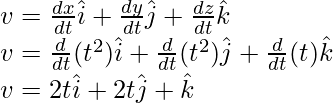
At t = 2,
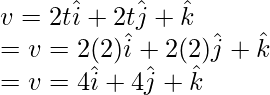
Question 2: Find the velocity at t = 0, for the particle which is moving in a plane and whose position is given, r = (t+2)i + (4t2+2)j + t2k
Answer:
Given: the initial and final position vectors,
r = (t+2)i + (4t2+2)j + t2k
The velocity in this case is given by the formula,
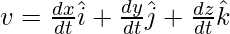
Here x(t) = (t + 2) and y(t) = 4t2 + 2and z(t) = t2
Plugging these values into the equation,
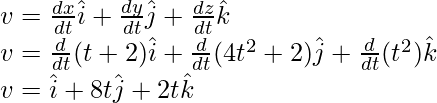
At t = 0,
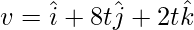
⇒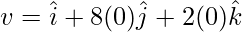
⇒ v = i
Question 3: Find the average acceleration between t = 0 and t = 3, for the particle which is moving in a plane and whose position is given, v = 3ti + 3t3j + k
Answer:
Given: velocity as a function of time.
v = 3ti + 3t3j + k
The velocity vector changes with time. The average acceleration is given by the formula,
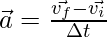
At t = 0
vi = 0i + 0j + k
At t = 3
vf = 9i + 81j + k
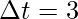
Plugging the values into the above equation,
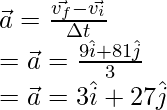
Question 4: Find the average acceleration between t = 0 and t = 2, for the particle which is moving in a plane and whose position is given, v = ti + 3tj + 2k
Answer:
Given: velocity as a function of time.
v = ti + 3tj + 2k
The velocity vector changes with time. The average acceleration is given by the formula,
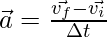
At t = 0
vi = 0i + 0j + 2k
At t = 2
vf = 2i + 6j + 2k
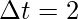
Plugging the values into the above equation,
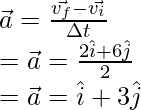
Question 5: Find the instantaneous acceleration at t = 1, for the particle which is moving in a plane and whose position is given, v = 2ti + 5t3j + tk
Answer:
Given: velocity as a function of time.
v = 2ti + 5t3j + tk
The velocity vector changes with time. The instantaneous acceleration is given by the formula,
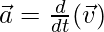
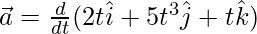
⇒ 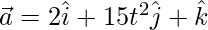
at t = 1,
⇒ 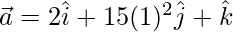
⇒ 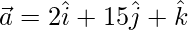
Share your thoughts in the comments
Please Login to comment...