For a rigid body, motion is generally both rotational and translation. If the body is fixed at one point, the motion is usually rotational. It is known that force is needed to change the translatory state of the body and to provide it with linear acceleration. Torque and angular momentum are rotational equivalents of force and momentum. These entities help us change the rotational state of the body. Torques and angular momentum are very useful and are encountered almost everywhere in daily life. The power of the engine and motors is measured by torque. So, while studying any rigid body, it is essential to understand the concepts of torque and angular momentum. Let’s look at these concepts in detail.
Torque
Torque is analogous to the force in the case of rotational motion. Consider an example of a door. The position of the door is fixed, it can only rotate around its axis. Then what causes the door to rotate? Force is required, but the force applied to the hinge of the door does not work. So, it is not the force alone, the position to which it is applied matters too.
In rotational motion, the analogous force is torque. This is also called the moment of force. This causes angular acceleration in the body, which means forcing to change the rotational state of the body. Let a particle P be located far from the origin at a point whose position vector is given by 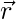 . If the force F is acting on the particle, the moment of force is given by,
. If the force F is acting on the particle, the moment of force is given by,
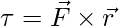
Since the cross-product is involved, it is a vector quantity. The magnitude of the torque is given by,
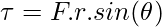
Here, “r” is the magnitude of the position vector, and θ is the angle between the position vector and force. In the formula, the part “rsinθ” is the perpendicular distance of the force from the axis of the rigid body.

Dimensions of torque are given by ML2T-2. These are also dimensions of energy but, these quantities should not be confused as similar. They are very different quantities.The unit of torque is N-m.
Angular Momentum of Particle
It has been mentioned that torque is analogous to force. In the same way, angular momentum is analogous to linear momentum. This is also a vector product similar to its counterpart torque. Consider a particle P with the linear momentum “p” and a position vector with respect to the origin O. The angular momentum of the particle is denoted by “L”,
L = r × p
The magnitude of angular momentum will be given by,
L = rpsinθ
Where r and p are the magnitudes of the position vector and linear momentum respectively. The angle θ is the angle between the position vector and the linear momentum. Here also “rsin(θ)” is the perpendicular angle between the momentum and the position vector.
Relationship between Angular Momentum and Torque
The relationship between the angular momentum and torque is similar to the relationship between the force and the momentum. Force is the change in momentum of the particle. Similarly, torque is the change in angular momentum of the particle. Differentiating the formula for the angular momentum,
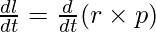
Applying the product rule for differentiation,
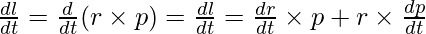
Now, 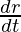 is the velocity of the particle, but since it is in the same direction as the momentum,
is the velocity of the particle, but since it is in the same direction as the momentum,
r x 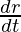 = 0
= 0
So, now the equation becomes,
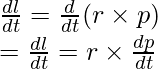
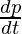 represents the force F,
represents the force F,
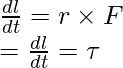
Thus, this proves that the rate of change of angular momentum is given by torque.
Sample Problems
Question 1: Find out the torque on the door if a force of 10N is applied on the door 0.5m from the hinge.
Answer:
Torque is given by,
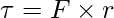
Where r is the perpendicular distance of the force from the rotational axis.
Given: r = 0.5m and F = 10N.
Plugging the values in the equation,
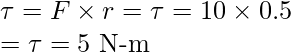
Question 2: Find out the torque on the door if a force of 20N is applied on the door 0.3m from the hinge.
Answer:
Torque is given by,
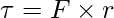
Where r is the perpendicular distance of the force from the rotational axis.
Given: r = 0.3m and F = 20N.
Plugging the values in the equation,
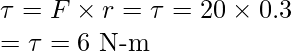
Question 3: A body is revolving around an axis in a circular motion with a radius of 0.1m, the momentum of the body is given by 50 Kgm/s. Find the angular momentum of the body.
Answer:
Angular momentum of a body is given by,
l = r × p
Where r is the perpendicular distance of the force from the rotational axis and p is the linear momentum.
Given: r = 0.3m and p = 50Kgm/s.
Plugging the values in the equation,
l = r xp
⇒l =0.3 × 50
⇒l = 15
Question 4: A body is revolving around an axis in a circular motion with a radius of 0.2m, the momentum of the body is given by 70 Kg/s. Find the angular momentum of the body.
Answer:
Angular momentum of a body is given by,
l = r × p
Where r is the perpendicular distance of the force from the rotational axis and p is the linear momentum.
Given: r = 0.2m and p =70 Kg/s.
Plugging the values in the equation,
l = r × p
⇒l =0.2 × 70
⇒l = 14
Question 5: A body is revolving around an axis in a circular motion with a radius of 0.2m, the momentum of the body is given by 70 Kg/s. A torque is applied on the body for 2 seconds and the momentum becomes 120Kgm/s. Find the torque applied to the body.
Answer:
Angular momentum of a body is given by,
l = r × p
Where r is the perpendicular distance of the force from the rotational axis and p is the linear momentum.
Rate of Change in angular momentum gives us the torque.
Initial angular momentum
li = 0. 2 × 70
li = 14
Final angular momentum
li = 0. 2 × 120
li = 24
Rate of change of angular momentum = 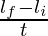
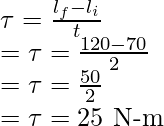
Question 6: A body is revolving around an axis in a circular motion with a radius of 0.1m, the momentum of the body is given by 50 Kgm/s. A torque is applied on the body for 4 seconds and the momentum becomes 100Kgm/s. Find the torque applied to the body.
Answer:
Angular momentum of a body is given by,
l = r × p
Where r is the perpendicular distance of the force from the rotational axis and p is the linear momentum.
Rate of Change in angular momentum gives us the torque.
Initial angular momentum
li = 0. 1 × 50
li = 5
Final angular momentum
li = 0. 1 × 100
li = 10
Rate of change of angular momentum = 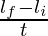
Share your thoughts in the comments
Please Login to comment...