Equations of Motion was given by Sir Issac Newton; who is considered the father of mechanics. He was the first to give the fundamental physical laws that deal with objects and their motion. He formulated three equations of motion of an object and published them in his book Philosophiae Naturalis Principia Mathematica, which is considered the starting point in the history of classical mechanics.
What are Equations of Motion?
In the year 1687, Sir Issac Newton published his book, and in his book, he wrote about his understanding of motion in the physical world as Newton’s Law of Motion. These laws alongside the Equations published gave the world an understanding of the motion of objects as well as their intersection with each other.
Definition of Equations of Motion
Equations of motion are mathematical equations that explain how a physical system behaves over time. Equations of Motion are used to describe the motion of objects and systems in terms of dynamic variables. In simpler terms, equations of motion use mathematical functions to describe how a physical system behaves.
Sir Isaac Newton gave three equations of motion. These equations are commonly known as the first, second, and third equations of motion, and they are described in detail below.
- First Equation of Motion
- Second Equation of Motion
- Third Equation of Motion
First Equation of Motion
The first equation of motion; which provides the relationship between the initial and final velocity, time, and acceleration, is as follows:
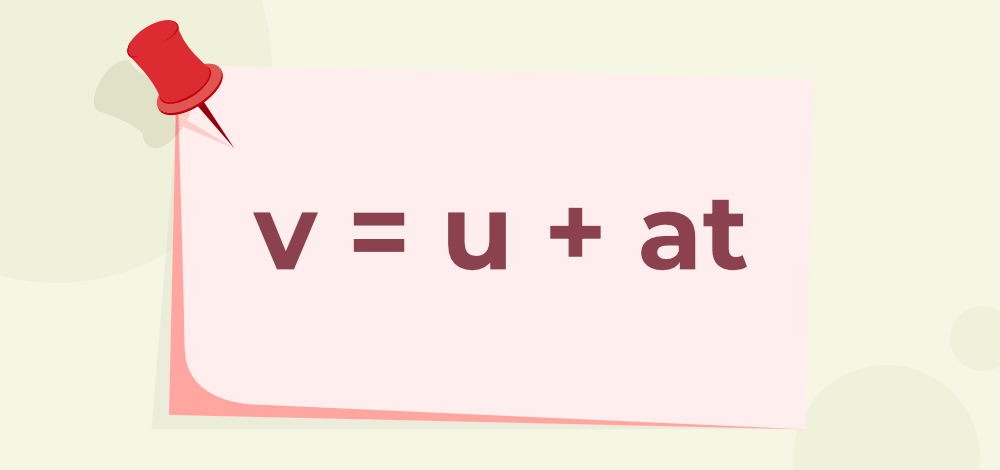
Second Equation of Motion
The second equation of motion; which provides the relationship between displacement, time, acceleration, and initial velocity, is as follows:
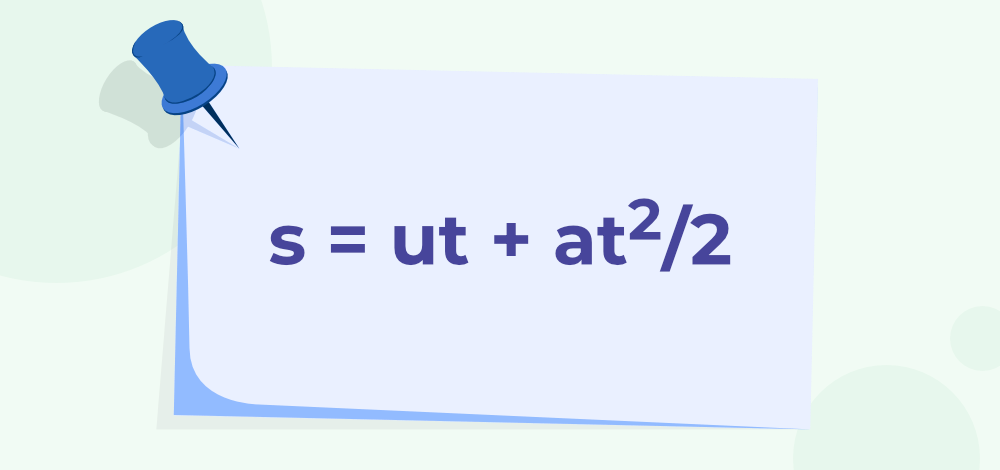
Third Equation of Motion
The Third equation of motion; which provides the relationship between initial and final velocity, acceleration, and displacement, is as follows:
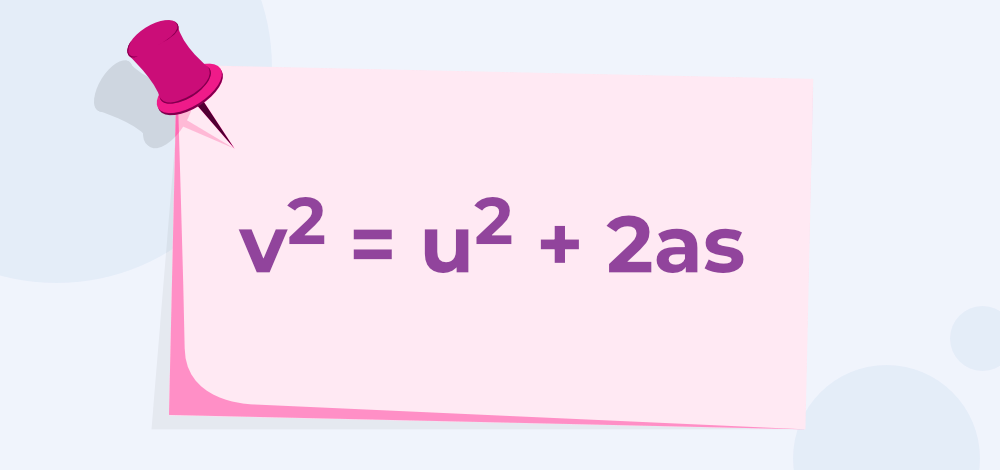
In the above equations, v is the final velocity (unit- meter per second), u is the initial velocity (unit- meter per second), a is the acceleration (unit- meter per second2), and s is the displacement (unit- meters) and t is the time (unit- second).
Derivation of Equations of Motion
We can derive the equation of motion by using three methods, which are as follows:
- Graphical Method
- Algebraic Method
- Calculus Method
Derivation of First Equation of Motion
The derivation of first equation of motion by different methods is mentioned below:
By Graphical Method
Read, Equations of Motion by Graphical Method

As slope of velocity-time graph represents acceleration.
Slope of graph = AB/BC
According to graph,
AB = v-u, and BC = t
⇒ a = (v-u)/t
⇒ at = v-u
⇒ v = u+at
By Algebraic Method
As we know the acceleration is defined as rate change of velocity, so if velocity changes from u to v in time t, then
a = change in velocity/time taken
⇒ a = (v-u)/t
⇒ at = v-u
⇒ v = u + at
By Calculus Method
By the definition of acceleration, it is defined as the rate of change in velocity.
Mathematically it can be expressed as :
a = dv/dt
Multiply dt on both sides,
⇒ adt = dv
Integrating on both sides, we get (the limit of dv is u to v and limit of dt is 0 to t)
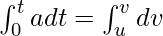
⇒ at = v – u
⇒ v = u + at
Derivation of Second Equation of Motion
The derivation of second equation of motion by different methods is mentioned below:
By Graphical Method
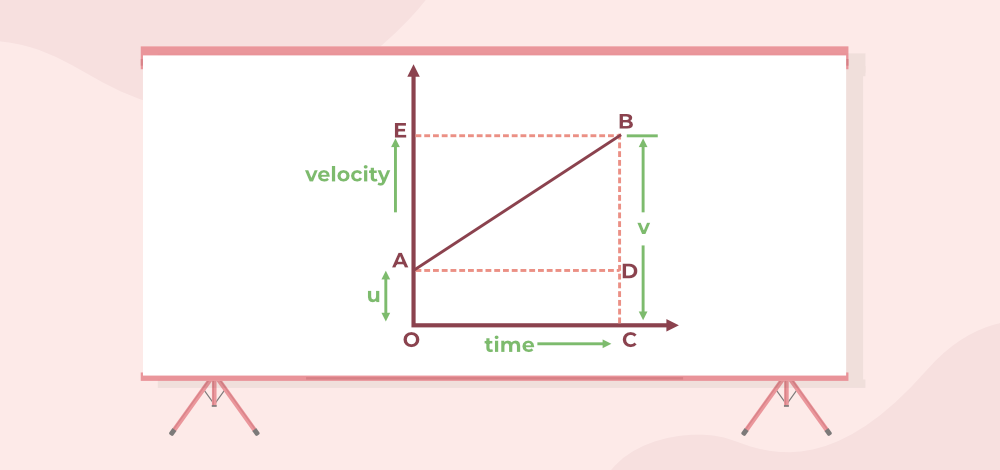
The area under the graph is the displacement of the body.
Distance travelled (s) = Area of OADC= Area of OADC + Area of ABD
⇒ s = (AD × BD × 1/2) + (OA × OC)
According to the graph
OA = u, OC = t, AD = t, BD = v-u
⇒ s = (t × at × 1/2) + ut
⇒ s = ut + at/2
By Algebraic Method
As displacement is the shortest distance between final and initial position, and given by the product of avrage velocity and time taken
that can be mathematically represented as, s = (u+v)/2×t . . .(i)
From first equation of motion, v=u+at
Equation (i) become,
s = (u+u+at)/2×t
⇒ s = (2u+at)/2×t
⇒ s = ut+at2/2
By Calculus Method
As velocity is known as the rate of change of displacement,
v=ds/dt
Multiply dt on both sides,
⇒ ds = vdt
From first equation of motion, Substituting v=u+at
ds = (u+at)dt
⇒ ds = udt+atdt
Integrating both sides,(limit of ds is 0 to s and limit of dt is 0 to t)
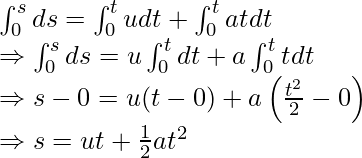
Derivation of Third Equation of Motion
The derivation of third equation of motion by different methods is mentioned below:
By Graphical Method

The area under the Graph is the displacement of the body.
Area under the Graph = Area of the trapezium OABC
⇒ s = (1/2) × ((Sum of Parallel Sides) × Height
⇒s = 1/2 × (OA + CB) × OC
From the Graph
OA = u, CB = v, OC = t
⇒ s = 1/2 × (u + v) × t
We know from the first equation of motion, t = (v – u)/ a
⇒ s = 1/2 × ((u + v) × (v – u))/a
⇒ s = 1/2 × (v + u) × (v – u)/a
⇒ s = (v2 – u2)/2a
⇒ 2as = v2– u2
⇒ v2= u2+2as
By Algebraic Method
As displacement is the shortest distance between final and initial position, and given by the product of avrage velocity and time taken
that can be mathematically represented as, s = (u+v)/2×t . . .(i)
As rearranging the first equation of motion, we get t = (v-u)/a
Substituting, t = (v-u)/a in equation (i), we get
s = (u+v)/2 × (v-u)/a
⇒ 2as = (v+u)(v-u)
⇒ 2as = v2-u2
⇒ v2=u2+2as
By Calculus Method
As velocity is known as the rate of change of displacement,
v=ds/dt . . .(i)
and acceleration is defined as the rate of change in velocity.
a = dv/dt . . .(ii)
From (i) and (ii), we get
a ds/dt = v dv/dt
⇒ a ds = v dv
Integrating both sides, we get( limit of ds is 0 to s and limit of dv is u to v)
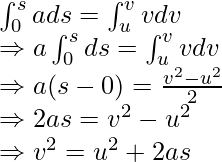
Solved Examples on Equations of Motion
Example 1: Mahesh throws the ball in the horizontal direction. If the ball travels 60 meters in 4 seconds they calculate the acceleration.
Solution:
As the body is thrown that means the initial velocity is zero.
⇒ u = 0
The distance traveled by the ball is displacement.
⇒ s = 80 meters
The time period is t = 4 s.
By using the equation, s = ut + at2/2
⇒ 80 = 0(4) + a(4)2/2
⇒ 80 = 8a
⇒ a=10 m/s2
Therefore the acceleration of the body after is 10 m/s2.
Example 2: A body is moving with a constant acceleration of 10 m/s2. If the initial velocity of the body is 5 m/s then what will be its velocity after 2 seconds?
Solution:
The acceleration of the body is 10 m/s2
⇒ a = 10 m/s2
The initial velocity is 5 m/s.
⇒ u = 5 m/s
The time period is 2 sec.
⇒ t = 2 sec
By using the equation, v = u + at
⇒ v = 5 + 10(2)
⇒ v = 5 + 20
⇒ v = 25 m/s
Therefore the velocity of the body after 2 seconds is 25 m/s.
Example 3: A body is moving with a constant acceleration of 10 m/s2. If the initial velocity of the body is 5 m/s and the final velocity is 105 m/s then what will be its displacement?
Solution:
The acceleration of the body is 10 m/s2.
⇒ a = 10
The initial velocity is 5 m/s.
⇒ u = 5 m/s
The final velocity is 105 m/s.
⇒ v = 105 m/s
By using the equation, v2 – u2 = 2as
⇒ 1052 – 52 = 2(10)(s)
⇒ s = (11025 – 25)/20
⇒ s = 550 sec
Therefore the time period is 550 seconds.
Example 4: What will be the displacement of a body if the initial and final velocities are 20 and 70 m/s respectively in 5 seconds?
Solution:
The initial velocity is 20 m/s.
⇒ u = 20 m/s
The final velocity is 170 m/s.
⇒ v = 70 m/s
The time period is 5 sec.
⇒ t = 5 sec
By using the equation, s = (1/2) (v + u)t
⇒ s = (0.5) (70 + 20)(5)
⇒ s = 550 meters
Therefore the displacement of a body is 550 meters.
Example 5: A car is moving with a velocity of 50 m/s when the driver sees a person crossing the road applies brakes and the car stops after 4 seconds. Calculate the distance traveled by car.
Solution:
The initial velocity is 50 m/s.
⇒ u = 50 m/s
The final velocity is 0 m/s.
⇒ v = 0 m/s
The time period is 4 seconds.
⇒ t = 4s
By using the equation, s = (1/2)(v + u)t
⇒ s = (0.5)(50 + 0)(4)
⇒ s = 100 meters
Therefore the displacement of the body is 100 m.
Example 6: A car is decelerating at 6m/s2. What is the distance traveled by the car if the initial speed is 20 m/s and the time taken to stop the car is 3 seconds?
Solution:
The deceleration of the body is 6 m/s2
⇒ a = 6
The initial velocity is 20 m/s.
⇒ u= 20 m/s
The time period is 3 sec.
⇒ t = 3 sec
By using the equation, s = ut – at2/2
⇒ s = 20(3) + 6(3)2/2
⇒ s = 60+27
⇒ s = 87 m
Therefore the displacement of the body is 87 m.
Numericals on Equations of Motion
1. An object starts from rest and accelerates at 2 m/s² for 5 seconds. Calculate its final velocity.
2. A car accelerates from 20 m/s to 30 m/s in 4 seconds. What is its acceleration?
3. A stone is dropped from a height of 100 meters. Calculate the time it takes to reach the ground.
4. A train is moving at a constant speed of 72 km/h. How long will it take to cover a distance of 360 kilometers?
5. A rocket accelerates from rest at a rate of 30 m/s² for 10 seconds. What is the final velocity of the rocket, and how far has it traveled during this time?
6. An object is thrown vertically upward with an initial velocity of 15 m/s. Calculate the time it takes for the object to reach its maximum height.
FAQs on Equations of Motion
1. What are the Equations of Motion?
The three equations,
- v=u+at
- s = ut + at2/2
- v2 – u2 = 2as
are combinedly called equations of motion.
2. What does the Area under the Velocity-Time Graph represent?
Area under the velocity-time graph represents the acceleration of the object for which the graph is drawn.
3. What does the Area under the Displacement-Time Graph represent?
Area under the displacement-time graph represents the magnitude of displacement of the object for which the graph is drawn.
4. What does the Slope of the Displacement-Time Graph represent?
Slope of the displacement-time graph represents the velocity of the object for which the graph is drawn.
5. What does the Slope of the Velocity-Time Graph represent?
Slope of the velocity-time graph represents the acceleration of the object for which the graph is drawn.
6. What is the First Equation of Motion?
The first equation of motion is given as:
v = u + at
Where,
v = final velocity
u = initial velocity
a = acceleration
t = time taken
7. What is the Second Equation of Motion?
The first equation of motion is given as:
S = ut + 1/2at2
Where,
v = final velocity
u = initial velocity
a = acceleration
t = time taken
8. What is the Third Equation of Motion?
The first equation of motion is given as:
v2 = u2 + 2as
Where,
v = final velocity
u = initial velocity
a = acceleration
t = time taken
9. Is Equation of Motion important for Class 9?
Yes, Equations of Motion is a very important topic for class 8 and class 9.
Share your thoughts in the comments
Please Login to comment...