Law of Conservation of Energy is the most fundamental law of physics which states that “Energy can neither be created nor be destroyed it can only change from one form of the energy to another form of the energy.” It is the fundamental law of Physics that governs various processes in our environment.
Before learning deeply about the Law of Conservation of Energy we must know about Energy. Energy is the capacity of the object to do work, It is a physical quantity that allows an object to do different types of work.
Let’s learn more about the Law of Conservation of Energy, and others in detail in this article.
What is Energy?
Energy is that ability that helps in applying force in order to do some work. It is simply that force that causes things to move. The capacity to do work is known as Energy. One very important fact about energy to note is that even though, energy occurs in many forms and has so many types, from kinetic energy to potential energy to solar energy, etc. The SI Unit of energy is Joules. Apart from joules, other units of Energy are ⇢ Calories, Horsepower, Kilowatt (kW)-Power, and Kilowatt-hour (kWh). There are many different forms of energy, following list shows and describes some of the important aspects of mechanical energy:
- Kinetic Energy: Kinetic Energy is the energy that is possessed by the objects in motion. Work must be done on an object to change its kinetic energy. It is usually expressed in the form of the equation 1/2mv2.
- Potential Energy: Potential energy is defined as the energy that is possessed by an object by virtue of its position. The potential energy is denoted by “mgh” where “h” is the height of the object.
- Mechanical Energy: This energy is the total energy associated with the position and velocity that is stored in the object. Hence, mechanical energy is the sum of kinetic energy and potential energy.
- Chemical Energy: Chemical energy is defined as the energy that is stored inside the bonds in the materials. This energy is involved in the formation or destruction of chemical bonds.
- Nuclear Energy: This energy is defined as the energy that is produced or consumed in the processes where nuclei of atoms are involved.
Energy Conservation
From the above examples, it is clear that the total energy of the system is always conserved it can only be converted from one form to another. It wastes lots of our energy by converting one form of energy into another form. So we must use our energy resources widely this is called energy conservation.
What is the Law of Conservation of Energy?
It’s known that the total mechanical energy of the system remains constant if the forces working on the system are conservative in nature. Potential energy and kinetic energies keep interchanging with each other. In the case of non-conservative forces, these energies are converted to some other energy such as heat, noise, etc. In the case of a system that is isolated from the outside world, the total energy remains constant.
In an isolated system, energy can neither be created nor be destroyed. Total energy remains constant. It can be converted from one form to another form.
The principles of conservation of energy cannot be proved however no violation of this law has ever been observed. So, it is widely accepted with proof.
For an isolated system, the loss of energy in some part is followed by a gain of an equal amount of energy in some other part of the system. This principle is not yet proven but no exception of this principle is yet encountered by physicists so it is considered to be true.
The law of conservation of energy can easily be understood by the following example, here in the image given below the total energy of the cyclist at the bottom of the hill is in the form of Kinetic Energy only, and at the top of the hill is in form of potential energy.
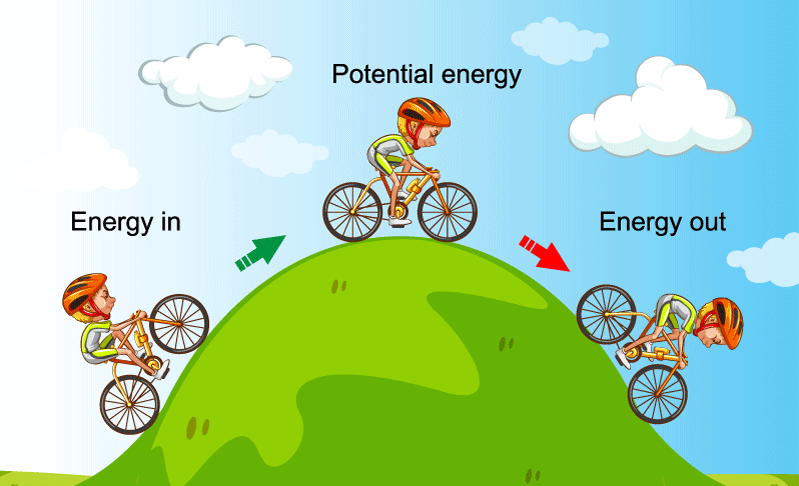
The total amount of energy in any system is calculated using the following equation:
UT = Ui + W + Q
Where,
- UT is total energy of a system,
- Ui is initial energy of a system,
- Q is heat added or removed from the system, and
- W is work done by or on the system.
Also, change in the internal energy of the system is calculated using,
ΔU = W + Q
Law of Conservation of Energy Derivation
Law of Conservation of Energy can be derived with the help of the following example, take a ball falling from the height H and the initial velocity is zero, also the potential energy at the surface of the earth is zero.
Now at the height H from the ground,
Etotal = Epotential + Ekinetic
⇒ Etotal = 1/2mv2 + mgH
⇒ Etotal = 1/2m(0)2 + mgH
⇒ Etotal = mgH…(A)
As the ball falls to the ground, its potential energy decreases, and kinetic energy increases.
At any point B, which is at a height X from the ground, it has speed ‘v’ as it reaches point B. So, at this point, it has both kinetic and potential energy.
Etotal = Epotential + Ekinetic…(1)
and Epotential = mgX…(2)
According to the third equation of motion,
v2 = 2g(H-X)
⇒ 1/2mv2 = 1/2m×2g(H-X)
⇒ 1/2mv2 = mg(H-X)
⇒ Ekinetic = mg(H-X)…(2)
Using (1), (2), and (3)
E = mg(H – X) + mgX
⇒ E = mg(H – X + X)
⇒ E = mgH…(B)
Also, at point C, at the ground,
Etotal = Epotential + Ekinetic…(a)
⇒ Epotential = 0…(b) (as height is zero)
According to the third equation of motion,
v2 = 2g(H-0)
⇒ 1/2mv2 = 1/2m×2g(H)
⇒ 1/2mv2 = mg(H)
⇒ Ekinetic = mg(H)…(c)
Using (a), (b), and (c)
E = mg(H) + 0
⇒ E = mgH…(C)
Thus, from A, B, and C it is clear that the total energy at any point of the falling of the ball is constant (mgH).
Law of Conservation of Energy Examples
Various events or examples we see in our daily life support the Law of Conservation of Energy. Some of the examples to prove the law of Conservation of Energy are discussed below in this article.
- Engines convert chemical energy into mechanical energy.
- An electric motor converts electrical energy into mechanical energy.
- Electric bulb converts electric energy into light and heat energy.
- Hydroelectric power plants convert the potential energy of water into the kinetic energy of the turbine, which is further converted into electrical energy.
- Loudspeaker converts electrical energy into sound energy and some portion of the energy is dissipated in the form of heat.
- An electrochemical cell converts chemical energy into electric energy and vice versa.
Application of Conservation of Energy
There are various applications for the conservation of Energy as it is widely used in various processes which we observed in our daily life. Some of the processes in which conservation of energy is applied are,
- A car engine converts the chemical energy of the fuel into mechanical energy and enables the car to run.
- The energy we get from the food we eat is an example of conservation of energy as the chemical energy of the food is changed into various forms of energy by our body to do various life processes.
- A hydroelectric power dam uses the potential energy of the water to rotate its turbine which in turn produces electrical energy.
- A moving car hits another car at rest transfers its energy to the other car and the other car gains some motion.
- A player hitting a ball from his bat uses his mechanical energy to give kinetic energy to the ball.
- An electric generator uses the chemical energy of the fuel to run its engine which in turn rotates a coil that produces electric energy.
In all the above examples the conservation of energy holds true as the energy in all the cases is neither created nor gets destroyed it only changes its form.
Why Can Perpetual Motion Machines Never Work?
We can create a machine that when given some energy must run for infinity only changing its form of energy. These types of machines are called perpetual machines and theoretically, they can run forever but the second law of thermodynamics does not allow for the making of these machines as every time the energy changes its form some of the energy gets wasted.
For, example if we create a Perpetual Motion Machines that take the potential energy of the water stored at some height and allow it to change that energy into mechanical energy which in turn uses this mechanical energy to store water again at that height, and this loop is continued till infinity. This is true in theoretical case but in reality, this machine loses some energy in the form of friction, air drag, and other, and in every cycle, a significant amount of energy gets wasted which in turn cause the machine to stop after some time.
Thus perpetual motion machines never work for infinite cycles and they only work for a finite cycle.
Also, Check
Solved Examples on Conservation of Energy
Example 1: Find the work done when a force of F = x + 3 produces a displacement of 3 m.
Solution:
Work done by a variable force is given by,
W = ∫Fdx
F(x) = x + 3
Calculating the work done.
W = [Tex]\int^{x}_{0}Fdx \\ = \int^{x}_{0}(x + 3)dx \\ = [\frac{x^2}{2} + 3x]^{x}_{0} \\ = \frac{x^2}{2} + 3x
[/Tex]
Here, the displacement is x = 3
W = x2/3 + 4x (at x = 3)
⇒ W = 32/3 + 4(3)
⇒ W = 15 J
Example 2: The work being done on a system is given by the following equation, W = 3t2
Calculate the instantaneous power at t = 4.
Solution:
Instantaneous power is given by,
P = dW/dt
Given: W = 3t2
Calculating power, P = dW/dt
[Tex]P = \frac{d(3t^2)}{dt}
[/Tex]
⇒ P = 6t
At, t = 4
P = 6(4)
⇒ P = 24 J
Example 3: The work being done on a system is given by the following equation, W = t3 + 5t + 10
Calculate the instantaneous power at t = 2.
Solution:
Instantaneous power is given by,
P = dW/dt
Given:
W = t3 + 5t + 10
Calculating power,
P = dW/dt
⇒ [Tex]P = \frac{d(t^3 + 5t + 10)}{dt}
[/Tex]
⇒ P = 3t2 + 5
At, t = 2
P = 3(t2) + 5
⇒ P = 3(22) + 5 J
⇒ P = 3(4) + 5
⇒ P = 17 J
Example 4: An object is kept at a height of 20m. It starts falling towards the ground. Find the velocity of the object just before it touches the ground.
Solution:
Potential energy at the start will be equal to the kinetic energy just before touching the ground.
P. E = K. E
mgh = 1/2mv2
Given:
g = 10
h = 20 m
Plugging the values inside the equation,
mgh = 1/2mv2
⇒ 2gh = v2
⇒ v = [Tex]\sqrt{2gh}
[/Tex]
⇒ v = [Tex]\sqrt{2 \times 10 \times 20}
[/Tex]
⇒ v = 20 m/s.
Law of Conservation of Energy – FAQs
What is Energy?
The ability of a body to do work is called energy.
State the Law of Conservation of Energy?
Law of conservation of energy states, that foe a closed system the total energy of the system is always conserved.
What are some Examples of the Law of Conservation of Energy?
Various examples explaining the law of conservation of energy include,
- Hydroelectric power plants convert potential energy to electrical energy.
- The loudspeaker converts electrical energy into sound energy.
- An electric motor converts electric energy into mechanical energy, etc.
Who Discovered the Law of Conservation of Energy?
Julius Robert Mayer was credited with the discovery of the law of conservation of energy.
Which Types of Energy can be seen when a Block Slides Down a Slope?
When a block slides down a slope, potential energy is converted into kinetic energy.
Give an Example where Potential Energy is Converted into Kinetic Energy.
In rocket propulsion, the chemical potential energy of the fuel is converted into kinetic energy of the exhasust gases which provide the required upthrust to the rocket.
Share your thoughts in the comments
Please Login to comment...