Count set bits in an integer
Last Updated :
11 Apr, 2023
Write an efficient program to count the number of 1s in the binary representation of an integer.
Examples :
Input : n = 6
Output : 2
Binary representation of 6 is 110 and has 2 set bits
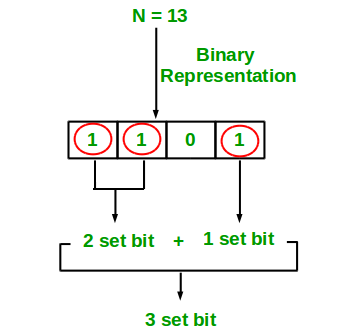
Input : n = 13
Output : 3
Binary representation of 13 is 1101 and has 3 set bits
1. Simple Method Loop through all bits in an integer, check if a bit is set and if it is, then increment the set bit count. See the program below.
C++
#include <bits/stdc++.h>
using namespace std;
unsigned int countSetBits(unsigned int n)
{
unsigned int count = 0;
while (n) {
count += n & 1;
n >>= 1;
}
return count;
}
int main()
{
int i = 9;
cout << countSetBits(i);
return 0;
}
|
C
#include <stdio.h>
unsigned int countSetBits(unsigned int n)
{
unsigned int count = 0;
while (n) {
count += n & 1;
n >>= 1;
}
return count;
}
int main()
{
int i = 9;
printf("%d", countSetBits(i));
return 0;
}
|
Java
import java.io.*;
class countSetBits {
static int countSetBits(int n)
{
int count = 0;
while (n > 0) {
count += n & 1;
n >>= 1;
}
return count;
}
public static void main(String args[])
{
int i = 9;
System.out.println(countSetBits(i));
}
}
|
Python3
def countSetBits(n):
count = 0
while (n):
count += n & 1
n >>= 1
return count
i = 9
print(countSetBits(i))
|
C#
using System;
class GFG {
static int countSetBits(int n)
{
int count = 0;
while (n > 0) {
count += n & 1;
n >>= 1;
}
return count;
}
public static void Main()
{
int i = 9;
Console.Write(countSetBits(i));
}
}
|
PHP
<?php
function countSetBits($n)
{
$count = 0;
while ($n)
{
$count += $n & 1;
$n >>= 1;
}
return $count;
}
$i = 9;
echo countSetBits($i);
?>
|
Javascript
<script>
function countSetBits(n)
{
var count = 0;
while (n)
{
count += n & 1;
n >>= 1;
}
return count;
}
var i = 9;
document.write(countSetBits(i));
</script>
|
Time Complexity: O(log n)
Auxiliary Space: O(1)
Recursive Approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countSetBits(int n)
{
if (n == 0)
return 0;
else
return (n & 1) + countSetBits(n >> 1);
}
int main()
{
int n = 9;
cout << countSetBits(n);
return 0;
}
|
C
#include <stdio.h>
int countSetBits(int n)
{
if (n == 0)
return 0;
else
return (n & 1) + countSetBits(n >> 1);
}
int main()
{
int n = 9;
printf("%d", countSetBits(n));
return 0;
}
|
Java
import java.io.*;
class GFG {
public static int countSetBits(int n)
{
if (n == 0)
return 0;
else
return (n & 1) + countSetBits(n >> 1);
}
public static void main(String[] args)
{
int n = 9;
System.out.println(countSetBits(n));
}
}
|
Python3
def countSetBits( n):
if (n == 0):
return 0
else:
return (n & 1) + countSetBits(n >> 1)
n = 9
print( countSetBits(n))
|
C#
using System;
class GFG {
public static int countSetBits(int n)
{
if (n == 0)
return 0;
else
return (n & 1) + countSetBits(n >> 1);
}
static public void Main()
{
int n = 9;
Console.WriteLine(countSetBits(n));
}
}
|
PHP
<?php
function countSetBits($n)
{
if ($n == 0)
return 0;
else
return ($n & 1) +
countSetBits($n >> 1);
}
$n = 9;
echo countSetBits($n);
?>
|
Javascript
<script>
function countSetBits(n)
{
if (n == 0)
return 0;
else
return (n & 1) + countSetBits(n >> 1);
}
let n = 9;
document.write(countSetBits(n));
</script>
|
Time Complexity: O(log n)
Auxiliary Space: O(log n) for recursive stack space
2. Brian Kernighan’s Algorithm:
Subtracting 1 from a decimal number flips all the bits after the rightmost set bit(which is 1) including the rightmost set bit.
for example :
10 in binary is 00001010
9 in binary is 00001001
8 in binary is 00001000
7 in binary is 00000111
So if we subtract a number by 1 and do it bitwise & with itself (n & (n-1)), we unset the rightmost set bit. If we do n & (n-1) in a loop and count the number of times the loop executes, we get the set bit count.
The beauty of this solution is the number of times it loops is equal to the number of set bits in a given integer.
1 Initialize count: = 0
2 If integer n is not zero
(a) Do bitwise & with (n-1) and assign the value back to n
n: = n&(n-1)
(b) Increment count by 1
(c) go to step 2
3 Else return count
Example for Brian Kernighan’s Algorithm:
n = 9 (1001)
count = 0
Since 9 > 0, subtract by 1 and do bitwise & with (9-1)
n = 9&8 (1001 & 1000)
n = 8
count = 1
Since 8 > 0, subtract by 1 and do bitwise & with (8-1)
n = 8&7 (1000 & 0111)
n = 0
count = 2
Since n = 0, return count which is 2 now.
Implementation of Brian Kernighan’s Algorithm:
C++
#include <iostream>
using namespace std;
class gfg {
public:
unsigned int countSetBits(int n)
{
unsigned int count = 0;
while (n) {
n &= (n - 1);
count++;
}
return count;
}
};
int main()
{
gfg g;
int i = 9;
cout << g.countSetBits(i);
return 0;
}
|
C
#include <stdio.h>
unsigned int countSetBits(int n)
{
unsigned int count = 0;
while (n) {
n &= (n - 1);
count++;
}
return count;
}
int main()
{
int i = 9;
printf("%d", countSetBits(i));
getchar();
return 0;
}
|
Java
import java.io.*;
class countSetBits {
static int countSetBits(int n)
{
int count = 0;
while (n > 0) {
n &= (n - 1);
count++;
}
return count;
}
public static void main(String args[])
{
int i = 9;
System.out.println(countSetBits(i));
}
}
|
Python3
def countSetBits(n):
count = 0
while (n):
n &= (n-1)
count+= 1
return count
i = 9
print(countSetBits(i))
|
C#
using System;
class GFG {
static int countSetBits(int n)
{
int count = 0;
while (n > 0) {
n &= (n - 1);
count++;
}
return count;
}
static public void Main()
{
int i = 9;
Console.WriteLine(countSetBits(i));
}
}
|
PHP
<?php
function countSetBits($n)
{
$count = 0;
while ($n)
{
$n &= ($n - 1) ;
$count++;
}
return $count;
}
$i = 9;
echo countSetBits($i);
?>
|
Javascript
<script>
function countSetBits(n)
{
var count = 0;
while (n > 0)
{
n &= (n - 1);
count++;
}
return count;
}
var i = 9;
document.write(countSetBits(i));
</script>
|
Time Complexity: O(log n)
Auxiliary Space: O(1)
Recursive Approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countSetBits(int n)
{
if (n == 0)
return 0;
else
return 1 + countSetBits(n & (n - 1));
}
int main()
{
int n = 9;
cout << countSetBits(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
public static int countSetBits(int n)
{
if (n == 0)
return 0;
else
return 1 + countSetBits(n & (n - 1));
}
public static void main(String[] args)
{
int n = 9;
System.out.println(countSetBits(n));
}
}
|
Python3
def countSetBits(n):
if (n == 0):
return 0
else:
return 1 + countSetBits(n & (n - 1))
n = 9
print(countSetBits(n))
|
C#
using System;
class GFG {
public static int countSetBits(int n)
{
if (n == 0)
return 0;
else
return 1 + countSetBits(n & (n - 1));
}
static public void Main()
{
int n = 9;
Console.WriteLine(countSetBits(n));
}
}
|
PHP
<?php
function countSetBits($n)
{
if ($n == 0)
return 0;
else
return 1 +
countSetBits($n &
($n - 1));
}
$n = 9;
echo countSetBits($n);
?>
|
Javascript
<script>
function countSetBits(n)
{
if (n == 0)
return 0;
else
return 1 + countSetBits(n & (n - 1));
}
var n = 9;
document.write(countSetBits(n));
</script>
|
Time Complexity: O(log n)
Auxiliary Space: O(log n)
3. Using Lookup table: We can count bits in O(1) time using the lookup table.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int BitsSetTable256[256];
void initialize()
{
BitsSetTable256[0] = 0;
for (int i = 0; i < 256; i++)
{
BitsSetTable256[i] = (i & 1) +
BitsSetTable256[i / 2];
}
}
int countSetBits(int n)
{
return (BitsSetTable256[n & 0xff] +
BitsSetTable256[(n >> 8) & 0xff] +
BitsSetTable256[(n >> 16) & 0xff] +
BitsSetTable256[n >> 24]);
}
int main()
{
initialize();
int n = 9;
cout << countSetBits(n);
}
|
Java
import java.util.*;
class GFG {
static int[] BitsSetTable256 = new int[256];
public static void initialize()
{
BitsSetTable256[0] = 0;
for (int i = 0; i < 256; i++) {
BitsSetTable256[i] = (i & 1) + BitsSetTable256[i / 2];
}
}
public static int countSetBits(int n)
{
return (BitsSetTable256[n & 0xff]
+ BitsSetTable256[(n >> 8) & 0xff]
+ BitsSetTable256[(n >> 16) & 0xff]
+ BitsSetTable256[n >> 24]);
}
public static void main(String[] args)
{
initialize();
int n = 9;
System.out.print(countSetBits(n));
}
}
|
Python
BitsSetTable256 = [0] * 256
def initialize():
BitsSetTable256[0] = 0
for i in range(256):
BitsSetTable256[i] = (i & 1) + BitsSetTable256[i // 2]
def countSetBits(n):
return (BitsSetTable256[n & 0xff] +
BitsSetTable256[(n >> 8) & 0xff] +
BitsSetTable256[(n >> 16) & 0xff] +
BitsSetTable256[n >> 24])
initialize()
n = 9
print(countSetBits(n))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int[] BitsSetTable256 = new int[256];
public static void initialize()
{
BitsSetTable256[0] = 0;
for (int i = 0; i < 256; i++)
{
BitsSetTable256[i] = (i & 1) + BitsSetTable256[i / 2];
}
}
public static int countSetBits(int n)
{
return (BitsSetTable256[n & 0xff]
+ BitsSetTable256[(n >> 8) & 0xff]
+ BitsSetTable256[(n >> 16) & 0xff]
+ BitsSetTable256[n >> 24]);
}
public static void Main(String[] args)
{
initialize();
int n = 9;
Console.Write(countSetBits(n));
}
}
|
Javascript
<script>
var BitsSetTable256 = Array.from({length: 256}, (_, i) => 0);
function initialize()
{
BitsSetTable256[0] = 0;
for (var i = 0; i < 256; i++) {
BitsSetTable256[i] = (i & 1) +
BitsSetTable256[parseInt(i / 2)];
}
}
function countSetBits(n)
{
return (BitsSetTable256[n & 0xff]
+ BitsSetTable256[(n >> 8) & 0xff]
+ BitsSetTable256[(n >> 16) & 0xff]
+ BitsSetTable256[n >> 24]);
}
initialize();
var n = 9;
document.write(countSetBits(n));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
We can find one use of counting set bits at Count number of bits to be flipped to convert A to B
Note: In GCC, we can directly count set bits using __builtin_popcount(). So we can avoid a separate function for counting set bits.
C++
#include <iostream>
using namespace std;
int main()
{
cout << __builtin_popcount(4) << endl;
cout << __builtin_popcount(15);
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
System.out.println(Integer.bitCount(4));
System.out.println(Integer.bitCount(15));
}
}
|
Python3
print(bin(4).count('1'));
print(bin(15).count('1'));
|
C#
using System;
class Program
{
static void Main(string[] args)
{
Console.WriteLine(Convert.ToString(4, 2).Replace("0", "").Length);
Console.WriteLine(Convert.ToString(15, 2).Replace("0", "").Length);
}
}
|
PHP
<?php
$t = log10(4);
$x = log(15, 2);
$tt = ceil($t);
$xx = ceil($x);
echo ($tt), "\n";
echo ($xx), "\n";
?>
|
Javascript
<script>
document.write((4).toString(2).split('').
filter(x => x == '1').length + "<br>");
document.write((15).toString(2).split('').
filter(x => x == '1').length);
</script>
|
Time complexity: O(1)
Auxiliary space: O(1)
4. Mapping numbers with the bit. It simply maintains a map(or array) of numbers to bits for a nibble. A Nibble contains 4 bits. So we need an array of up to 15.
int num_to_bits[16] = {0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4};
Now we just need to get nibbles of a given long/int/word etc recursively.
C++
#include <bits/stdc++.h>
using namespace std;
int num_to_bits[16] = { 0, 1, 1, 2, 1, 2, 2, 3,
1, 2, 2, 3, 2, 3, 3, 4 };
unsigned int countSetBitsRec(unsigned int num)
{
int nibble = 0;
if (0 == num)
return num_to_bits[0];
nibble = num & 0xf;
return num_to_bits[nibble] + countSetBitsRec(num >> 4);
}
int main()
{
int num = 31;
cout << countSetBitsRec(num);
return 0;
}
|
C
#include <stdio.h>
int num_to_bits[16] = { 0, 1, 1, 2, 1, 2, 2, 3,
1, 2, 2, 3, 2, 3, 3, 4 };
unsigned int countSetBitsRec(unsigned int num)
{
int nibble = 0;
if (0 == num)
return num_to_bits[0];
nibble = num & 0xf;
return num_to_bits[nibble] + countSetBitsRec(num >> 4);
}
int main()
{
int num = 31;
printf("%d\n", countSetBitsRec(num));
}
|
Java
import java.util.*;
class GFG {
static int[] num_to_bits = new int[] { 0, 1, 1, 2, 1, 2, 2,
3, 1, 2, 2, 3, 2, 3, 3, 4 };
static int countSetBitsRec(int num)
{
int nibble = 0;
if (0 == num)
return num_to_bits[0];
nibble = num & 0xf;
return num_to_bits[nibble] + countSetBitsRec(num >> 4);
}
public static void main(String[] args)
{
int num = 31;
System.out.println(countSetBitsRec(num));
}
}
|
Python3
num_to_bits =[0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4];
def countSetBitsRec(num):
nibble = 0;
if(0 == num):
return num_to_bits[0];
nibble = num & 0xf;
return num_to_bits[nibble] + countSetBitsRec(num >> 4);
num = 31;
print(countSetBitsRec(num));
|
C#
class GFG {
static int[] num_to_bits = new int[16] { 0, 1, 1, 2, 1, 2, 2,
3, 1, 2, 2, 3, 2, 3, 3, 4 };
static int countSetBitsRec(int num)
{
int nibble = 0;
if (0 == num)
return num_to_bits[0];
nibble = num & 0xf;
return num_to_bits[nibble] + countSetBitsRec(num >> 4);
}
static void Main()
{
int num = 31;
System.Console.WriteLine(countSetBitsRec(num));
}
}
|
PHP
<?php
$num_to_bits = array(0, 1, 1, 2, 1, 2, 2, 3,
1, 2, 2, 3, 2, 3, 3, 4);
function countSetBitsRec( $num)
{
global $num_to_bits;
$nibble = 0;
if (0 == $num)
return $num_to_bits[0];
$nibble = $num & 0xf;
return $num_to_bits[$nibble] +
countSetBitsRec($num >> 4);
}
$num = 31;
echo (countSetBitsRec($num));
?>
|
Javascript
<script>
var num_to_bits =[ 0, 1, 1, 2, 1, 2, 2,
3, 1, 2, 2, 3, 2, 3, 3, 4 ];
function countSetBitsRec(num)
{
var nibble = 0;
if (0 == num)
return num_to_bits[0];
nibble = num & 0xf;
return num_to_bits[nibble] + countSetBitsRec(num >> 4);
}
var num = 31;
document.write(countSetBitsRec(num));
</script>
|
Time Complexity: O(log n), because we have log(16, n) levels of recursion.
Storage Complexity: O(1) Whether the given number is short, int, long, or long long we require an array of 16 sizes only, which is constant.
5. Checking each bit in a number:
Each bit in the number is checked for whether it is set or not. The number is bitwise AND with powers of 2, so if the result is not equal to zero, we come to know that the particular bit in the position is set.
C
#include <stdio.h>
int countSetBits(int N)
{
int count = 0;
for (int i = 0; i < sizeof(int) * 8; i++) {
if (N & (1 << i))
count++;
}
return count;
}
int main()
{
int N = 15;
printf("%d", countSetBits(N));
return 0;
}
|
C++
#include <iostream>
using namespace std;
int countSetBits(int N)
{
int count = 0;
for (int i = 0; i < sizeof(int) * 8; i++) {
if (N & (1 << i))
count++;
}
return count;
}
int main()
{
int N = 15;
cout << countSetBits(N) << endl;
return 0;
}
|
Java
import java.util.*;
public class GFG
{
static int countSetBits(int N)
{
int count = 0;
for (int i = 0; i < 4 * 8; i++)
{
if ((N & (1 << i)) != 0)
count++;
}
return count;
}
public static void main(String[] args)
{
int N = 15;
System.out.println(countSetBits(N));
}
}
|
Python3
def countSetBits(N):
count = 0
for i in range(4*8):
if(N & (1 << i)):
count += 1
return count
N = 15
print(countSetBits(N))
|
C#
using System;
class GFG
{
static int countSetBits(int N)
{
int count = 0;
for (int i = 0; i < 4 * 8; i++)
{
if ((N & (1 << i)) != 0)
count++;
}
return count;
}
static void Main()
{
int N = 15;
Console.WriteLine(countSetBits(N));
}
}
|
Javascript
<script>
function countSetBits(N)
{
var count = 0;
for (i = 0; i < 4 * 8; i++)
{
if ((N & (1 << i)) != 0)
count++;
}
return count;
}
var N = 15;
document.write(countSetBits(N));
</script>
|
Time complexity: O(log n)
Auxiliary space: O(1)
6. Using power of 2:(efficient method to find for large value also)
Iterate from k to 0 , where k is the largest power of 2 such that pow(2, k) <= num . And check if the Bitwise AND of num and pow(2, i) is greater than zero or not. If it is greater than zero , Then i-th bit is set ,then increase the count by 1.
C++
#include <bits/stdc++.h>
using namespace std;
int findk(int n)
{ int k; int i=0; int val=pow(2,i);
while(val<=n)
{
k=i; i++;
val=pow(2,i);
}
return k;
}
int countSetBits(int N)
{
int count = 0;
int k=findk(N);
int val , x;
for (int i = k; i >= 0; i--)
{
val=pow(2,i);
x=val & N;
if(x > 0)
{ count++;
}
}
return count;
}
int main()
{
int N = 15;
cout << countSetBits(N) << endl;
return 0;
}
|
Java
import java.io.*;
public class GFG {
static int findk(int n)
{
int k = 0;
int i = 0;
int val = (int)Math.pow(2, i);
while (val <= n) {
k = i;
i++;
val = (int)Math.pow(2, i);
}
return k;
}
static int countSetBits(int N)
{
int count = 0;
int k = findk(N);
int val, x;
for (int i = k; i >= 0; i--) {
val = (int)Math.pow(2, i);
x = val
& N;
if (x > 0) {
count++;
}
}
return count;
}
public static void main(String[] args)
{
int N = 15;
System.out.println(countSetBits(N));
}
}
|
Python3
import math
def findk(n):
i = 0
val = math.pow(2, i)
while val <= n:
k = i
i += 1
val = math.pow(2, i)
return k
def countSetBits(N):
count = 0
k = findk(N)
for i in range(k, -1, -1):
val = int(math.pow(2, i))
x = val & N
if x > 0:
count += 1
return count
if __name__ == '__main__':
N = 15
print(countSetBits(N))
|
C#
using System;
class Program
{
static int FindK(int n)
{
int k = 0;
int i = 0;
int val = (int)Math.Pow(2, i);
while (val <= n)
{
k = i;
i++;
val = (int)Math.Pow(2, i);
}
return k;
}
static int CountSetBits(int N)
{
int count = 0;
int k = FindK(N);
int val, x;
for (int i = k; i >= 0; i--)
{
val = (int)Math.Pow(2, i);
x = val & N;
if (x > 0)
{
count++;
}
}
return count;
}
static void Main()
{
int N = 15;
Console.WriteLine(CountSetBits(N));
}
}
|
Javascript
function findk(n){
let k;
let i = 0;
let val = Math.pow(2,i);
while(val <= n){
k=i;
i++;
val = Math.pow(2,i);
}
return k;
}
function countSetBits(N){
let count = 0;
let k = findk(N);
let val;
let x;
for(let i = k; i>=0; i--){
val = Math.pow(2,i);
x = val & N;
if(x > 0) count++;
}
return count;
}
let N = 15;
console.log(countSetBits(N));
|
Time Complexity: O(logn)
Auxiliary Space: O(1)
Count set bits in an integer Using Lookup Table
Share your thoughts in the comments
Please Login to comment...