Solovay-Strassen method of Primality Test

We have already been introduced to primality testing in the previous articles in this series. 

• Introduction to Primality Test and School Method
• Fermat Method of Primality Test
• Primality Test | Set 3 (Miller–Rabin)

The Solovay–Strassen primality test is a probabilistic test to determine if a number is composite or probably prime. 
Before diving into the code we will need to understand some key terms and concepts to be able to code this algorithm.

Background:
Legendre Symbol: This symbol is defined as a pair of integers a and p such that p is prime. It is denoted by (a/p) and calculated as: 

      = 0    if a%p = 0
(a/p) = 1    if there exists an integer k such that k2 = a(mod p)
      = -1   otherwise.

Euler proved that: 

 (a/p) = a((p-1)/2)%p Condition (i)

Jacobian Symbol: This symbol is a generalization of the Legendre Symbol, where p is replaced by n where n is

n = p1k1 * .. * pnkn

, then the Jacobian symbol is defined as: 

(a/n) = ((a/p1)k1) * ((a/p2)k2) *.....* ((a/pn)kn)

If n is taken as a prime number, then the Jacobian is equal to the Legendre symbol. These symbols have certain properties – 
1) (a/n) = 0 if gcd(a,n) != 1, Hence (0/n) = 0. This is because if gcd(a,n) != 1, then there must be some prime pi such that pi divides both a and n. In that case (a/pi) = 0 [by definition of the Legendre Symbol]. 
2) (ab/n) = (a/n) * (b/n). It can be easily derived from the fact (ab/p) = (a/p)(b/p) (here (a/p) is the Legendry Symbol). 
3) If a is even, then (a/n) = (2/n)*((a/2)/n). It can be shown that: 

      = 1 if n = 1 ( mod 8 ) or n = 7 ( mod 8 )
(2/n) = -1 if n = 3 ( mod 8 ) or n = 5 ( mod 8 )
      = 0 otherwise

4) (a/n) = (n/a) * (-1)((a - 1)(n - 1) / 4)  if a and n are both odd.

The Algorithm:
We select a number n to test for its primality and a random number a which lies in the range of [2, n-1] and compute its Jacobian (a/n), if n is a prime number, then the Jacobian will be equal to the Legendre and it will satisfy the condition (i) given by Euler. If it does not satisfy the given condition, then n is composite and the program will stop. Just like every other Probabilistic Primality Test, its accuracy is also directly proportional to the number of iterations. So we ran the test for several iterations to get more accurate results.

Note: We are not interested in calculating the Jacobian of even numbers as we already know that they are not prime except 2.

Pseudocode:

Algorithm for Jacobian:
Step 1    //base cases omitted
Step 2     if a>n then
Step 3         return (a mod n)/n
Step 4     else

Step 5         return (-1)((a - 1)/2)((n - 1)/2)(a/n)
Step 6     endif

Algorithm for Solovay-Strassen:
Step 1    Pick a random element a < n
Step 2    if gcd(a, n) > 1 then
Step 3        return COMPOSITE
Step 4    end if
Step 5    Compute a(n - 1)/2 using repeated squaring
          and (a/n) using Jacobian algorithm.
Step 6    if (a/n) not equal to a(n - 1)/2 then
Step 7        return composite
Step 8    else
Step 9        return prime
Step 10   endif

Implementation:

C++

// C++ program to implement Solovay-Strassen
// Primality Test
#include <bits/stdc++.h>
using namespace std;

// modulo function to perform binary exponentiation
long long modulo(long long base, long long exponent,
                                      long long mod)
{
    long long x = 1;
    long long y = base;
    while (exponent > 0)
    {
        if (exponent % 2 == 1)
            x = (x * y) % mod;

        y = (y * y) % mod;
        exponent = exponent / 2;
    }

    return x % mod;
}

// To calculate Jacobian symbol of a given number
int calculateJacobian(long long a, long long n)
{
    if (!a)
        return 0;// (0/n) = 0

    int ans = 1;
    if (a < 0)
    {
        a = -a; // (a/n) = (-a/n)*(-1/n)
        if (n % 4 == 3)
            ans = -ans; // (-1/n) = -1 if n = 3 (mod 4)
    }

    if (a == 1)
        return ans;// (1/n) = 1

    while (a)
    {
        if (a < 0)
        {
            a = -a;// (a/n) = (-a/n)*(-1/n)
            if (n % 4 == 3)
                ans = -ans;// (-1/n) = -1 if n = 3 (mod 4)
        }

        while (a % 2 == 0)
        {
            a = a / 2;
            if (n % 8 == 3 || n % 8 == 5)
                ans = -ans;

        }

        swap(a, n);

        if (a % 4 == 3 && n % 4 == 3)
            ans = -ans;
        a = a % n;

        if (a > n / 2)
            a = a - n;

    }

    if (n == 1)
        return ans;

    return 0;
}

// To perform the Solovay-Strassen Primality Test
bool solovoyStrassen(long long p, int iterations)
{
    if (p < 2)
        return false;
    if (p != 2 && p % 2 == 0)
        return false;

    for (int i = 0; i < iterations; i++)
    {
        // Generate a random number a
        long long a = rand() % (p - 1) + 1;
        long long jacobian = (p + calculateJacobian(a, p)) % p;
        long long mod = modulo(a, (p - 1) / 2, p);

        if (!jacobian || mod != jacobian)
            return false;
    }
    return true;
}

// Driver Code
int main()
{
    int iterations = 50;
    long long num1 = 15;
    long long num2 = 13;

    if (solovoyStrassen(num1, iterations))
        printf("%d is prime\n",num1);
    else
        printf("%d is composite\n",num1);

    if (solovoyStrassen(num2, iterations))
        printf("%d is prime\n",num2);
    else
        printf("%d is composite\n",num2);

    return 0;
}

Java

// Java program to implement Solovay-Strassen
// Primality Test
import java.util.Scanner;
import java.util.Random;

class GFG{

// Modulo function to perform
// binary exponentiation
static long modulo(long base,
                   long exponent,
                   long mod)
{
    long x = 1;
    long y = base;

    while (exponent > 0)
    {
        if (exponent % 2 == 1)
            x = (x * y) % mod;

        y = (y * y) % mod;
        exponent = exponent / 2;

    }
    return x % mod;
}

// To calculate Jacobian symbol of
// a given number
static long calculateJacobian(long a, long n)
{
    if (n <= 0 || n % 2 == 0)
        return 0;

    long ans = 1L;

    if (a < 0)
    {
        a = -a; // (a/n) = (-a/n)*(-1/n)
        if (n % 4 == 3)
            ans = -ans; // (-1/n) = -1 if n = 3 (mod 4)
    }

    if (a == 1)
        return ans; // (1/n) = 1

    while (a != 0)
    {
        if (a < 0)
        {
            a = -a; // (a/n) = (-a/n)*(-1/n)
            if (n % 4 == 3)
                ans = -ans; // (-1/n) = -1 if n = 3 (mod 4)
        }

        while (a % 2 == 0)
        {
            a /= 2;
            if (n % 8 == 3 || n % 8 == 5)
                ans = -ans;
        }

        long temp = a;
        a = n;
        n = temp;

        if (a % 4 == 3 && n % 4 == 3)
            ans = -ans;

        a %= n;
        if (a > n / 2)
            a = a - n;
    }

    if (n == 1)
        return ans;

    return 0;
}

// To perform the Solovay-Strassen Primality Test
static boolean solovoyStrassen(long p,
                               int iteration)
{
    if (p < 2)
        return false;
    if (p != 2 && p % 2 == 0)
        return false;

    // Create Object for Random Class
    Random rand = new Random();
    for(int i = 0; i < iteration; i++)
    {

        // Generate a random number r
        long r = Math.abs(rand.nextLong());
        long a = r % (p - 1) + 1;
        long jacobian = (p + calculateJacobian(a, p)) % p;
        long mod = modulo(a, (p - 1) / 2, p);

        if (jacobian == 0 || mod != jacobian)
            return false;
    }
    return true;
}

// Driver code
public static void main (String[] args)
{
    int iter = 50;
    long num1 = 15;
    long num2 = 13;

    if (solovoyStrassen(num1, iter))
        System.out.println(num1 + " is prime");
    else
        System.out.println(num1 + " is composite");

     if (solovoyStrassen(num2,iter))
        System.out.println(num2 + " is prime");
    else
        System.out.println(num2 + " is composite");
}
}

// This code is contributed by Srishtik Dutta

Python3

# Python3 program to implement Solovay-Strassen
# Primality Test
import random

# modulo function to perform binary
# exponentiation
def modulo(base, exponent, mod):
    x = 1;
    y = base;
    while (exponent > 0):
        if (exponent % 2 == 1):
            x = (x * y) % mod;

        y = (y * y) % mod;
        exponent = exponent // 2;

    return x % mod;

# To calculate Jacobian symbol of a
# given number
def calculateJacobian(a, n):

    if (a == 0):
        return 0;# (0/n) = 0

    ans = 1;
    if (a < 0):

        # (a/n) = (-a/n)*(-1/n)
        a = -a;
        if (n % 4 == 3):

            # (-1/n) = -1 if n = 3 (mod 4)
            ans = -ans;

    if (a == 1):
        return ans; # (1/n) = 1

    while (a):
        if (a < 0):

            # (a/n) = (-a/n)*(-1/n)
            a = -a;
            if (n % 4 == 3):

                # (-1/n) = -1 if n = 3 (mod 4)
                ans = -ans;

        while (a % 2 == 0):
            a = a // 2;
            if (n % 8 == 3 or n % 8 == 5):
                ans = -ans;

        # swap
        a, n = n, a;

        if (a % 4 == 3 and n % 4 == 3):
            ans = -ans;
        a = a % n;

        if (a > n // 2):
            a = a - n;

    if (n == 1):
        return ans;

    return 0;

# To perform the Solovay- Strassen
# Primality Test
def solovoyStrassen(p, iterations):

    if (p < 2):
        return False;
    if (p != 2 and p % 2 == 0):
        return False;

    for i in range(iterations):

        # Generate a random number a
        a = random.randrange(p - 1) + 1;
        jacobian = (p + calculateJacobian(a, p)) % p;
        mod = modulo(a, (p - 1) / 2, p);

        if (jacobian == 0 or mod != jacobian):
            return False;

    return True;

# Driver Code
iterations = 50;
num1 = 15;
num2 = 13;

if (solovoyStrassen(num1, iterations)):
    print(num1, "is prime ");
else:
    print(num1, "is composite");

if (solovoyStrassen(num2, iterations)):
    print(num2, "is prime");
else:
    print(num2, "is composite");

# This code is contributed by mits

C#

/// C# program to implement Solovay-Strassen
// Primality Test
using System;
using System.Collections.Generic;
class GFG {

    // Modulo function to perform
    // binary exponentiation
    static long modulo(long Base, long exponent, long mod)
    {
        long x = 1;
        long y = Base;

        while (exponent > 0)
        {
            if (exponent % 2 == 1)
                x = (x * y) % mod;

            y = (y * y) % mod;
            exponent = exponent / 2;

        }
        return x % mod;
    }

    // To calculate Jacobian symbol of
    // a given number
    static long calculateJacobian(long a, long n)
    {
        if (n <= 0 || n % 2 == 0)
            return 0;

        long ans = 1L;

        if (a < 0)
        {
            a = -a; // (a/n) = (-a/n)*(-1/n)
            if (n % 4 == 3)
                ans = -ans; // (-1/n) = -1 if n = 3 (mod 4)
        }

        if (a == 1)
            return ans; // (1/n) = 1

        while (a != 0)
        {
            if (a < 0)
            {
                a = -a; // (a/n) = (-a/n)*(-1/n)
                if (n % 4 == 3)
                    ans = -ans; // (-1/n) = -1 if n = 3 (mod 4)
            }

            while (a % 2 == 0)
            {
                a /= 2;
                if (n % 8 == 3 || n % 8 == 5)
                    ans = -ans;
            }

            long temp = a;
            a = n;
            n = temp;

            if (a % 4 == 3 && n % 4 == 3)
                ans = -ans;

            a %= n;
            if (a > n / 2)
                a = a - n;
        }

        if (n == 1)
            return ans;

        return 0;
    }

    // To perform the Solovay-Strassen Primality Test
    static bool solovoyStrassen(long p, int iteration)
    {
        if (p < 2)
            return false;
        if (p != 2 && p % 2 == 0)
            return false;

        // Create Object for Random Class
        Random rand = new Random();
        for(int i = 0; i < iteration; i++)
        {

            // Generate a random number r
            long r = Math.Abs(rand.Next());
            long a = r % (p - 1) + 1;
            long jacobian = (p + calculateJacobian(a, p)) % p;
            long mod = modulo(a, (p - 1) / 2, p);

            if (jacobian == 0 || mod != jacobian)
                return false;
        }
        return true;
    }

  // Driver code
  static void Main()
  {
        int iter = 50;
        long num1 = 15;
        long num2 = 13;

        if (solovoyStrassen(num1, iter))
            Console.WriteLine(num1 + " is prime");
        else
            Console.WriteLine(num1 + " is composite");

         if (solovoyStrassen(num2,iter))
            Console.WriteLine(num2 + " is prime");
        else
            Console.WriteLine(num2 + " is composite");
  }
}

// This code is contributed by divyeshrabadiya07

PHP

<?php
// PHP program to implement
// Solovay-Strassen Primality Test

// modulo function to perform
// binary exponentiation
function modulo($base, $exponent, $mod)
{
    $x = 1;
    $y = $base;
    while ($exponent > 0)
    {
        if ($exponent % 2 == 1)
            $x = ($x * $y) % $mod;

        $y = ($y * $y) % $mod;
        $exponent = $exponent / 2;
    }

    return $x % $mod;
}

// To calculate Jacobian
// symbol of a given number
function calculateJacobian($a, $n)
{
    if (!$a)
        return 0;// (0/n) = 0

    $ans = 1;
    if ($a < 0)
    {
        // (a/n) = (-a/n)*(-1/n)
        $a = -$a;
        if ($n % 4 == 3)

            // (-1/n) = -1 if n = 3 (mod 4)
            $ans = -$ans;
    }

    if ($a == 1)
        return $ans;// (1/n) = 1

    while ($a)
    {
        if ($a < 0)
        {
            // (a/n) = (-a/n)*(-1/n)
            $a = -$a;
            if ($n % 4 == 3)

                // (-1/n) = -1 if n = 3 (mod 4)
                $ans = -$ans;
        }

        while ($a % 2 == 0)
        {
            $a = $a / 2;
            if ($n % 8 == 3 || $n % 8 == 5)
                $ans = -$ans;

        }
        //swap
        list($a, $n) = array($n, $a);

        if ($a % 4 == 3 && $n % 4 == 3)
            $ans = -$ans;
        $a = $a % $n;

        if ($a > $n / 2)
            $a = $a - $n;

    }

    if ($n == 1)
        return $ans;

    return 0;
}

// To perform the Solovay-
// Strassen Primality Test
function solovoyStrassen($p, $iterations)
{
    if ($p < 2)
        return false;
    if ($p != 2 && $p % 2 == 0)
        return false;

    for ($i = 0; $i < $iterations; $i++)
    {
        // Generate a random number a
        $a = rand() % ($p - 1) + 1;
        $jacobian = ($p +
                     calculateJacobian($a,
                                       $p)) % $p;
        $mod = modulo($a, ($p - 1) / 2, $p);

        if (!$jacobian || $mod != $jacobian)
            return false;
    }
    return true;
}

// Driver Code
$iterations = 50;
$num1 = 15;
$num2 = 13;

if (solovoyStrassen($num1, $iterations))
    echo $num1," is prime ","\n";
else
    echo $num1," is composite\n";

if (solovoyStrassen($num2, $iterations))
    echo $num2," is prime\n";
else
    echo $num2," is composite\n";

// This code is contributed by ajit
?>

Javascript

<script>

// Javascript program to implement Solovay-Strassen
// Primality Test


// Modulo function to perform
// binary exponentiation
function modulo( base, exponent,mod)
{
    let x = 1;
    let y = base;

    while (exponent > 0)
    {
        if (exponent % 2 == 1)
            x = (x * y) % mod;

        y = (y * y) % mod;
        exponent = Math.floor(exponent / 2);

    }
    return x % mod;
}

// To calculate Jacobian symbol of
// a given number
function calculateJacobian( a, n)
{
    if (n <= 0 || n % 2 == 0)
        return 0;

    let ans = 1;

    if (a < 0)
    {
        a = -a; // (a/n) = (-a/n)*(-1/n)
        if (n % 4 == 3)
            ans = -ans; // (-1/n) = -1 if n = 3 (mod 4)
    }

    if (a == 1)
        return ans; // (1/n) = 1

    while (a != 0)
    {
        if (a < 0)
        {
            a = -a; // (a/n) = (-a/n)*(-1/n)
            if (n % 4 == 3)
                ans = -ans; // (-1/n) = -1 if n = 3 (mod 4)
        }

        while (a % 2 == 0)
        {
            a = Math.floor(a/2);
            if (n % 8 == 3 || n % 8 == 5)
                ans = -ans;
        }

        let temp= a;
        a = n;
        n = temp;

        if (a % 4 == 3 && n % 4 == 3)
            ans = -ans;

        a %= n;
        if (a > Math.floor(n / 2))
            a = a - n;
    }

    if (n == 1)
        return ans;

    return 0;
}

// To perform the Solovay-Strassen Primality Test
function solovoyStrassen( p, iteration)
{
    if (p < 2)
        return false;
    if (p != 2 && p % 2 == 0)
        return false;


    for(let i = 0; i < iteration; i++)
    {

        // Generate a random number r
        let r = Math.floor(Math.random()* (Number.MAX_VALUE, 2) );
        let a = r % (p - 1) + 1;
        let jacobian = (p + calculateJacobian(a, p)) % p;
        let mod = modulo(a, Math.floor((p - 1) / 2), p);

        if (jacobian == 0 || mod != jacobian)
            return false;
    }
    return true;
}


// Driver Code

let iter = 50;
let num1 = 15;
let num2 = 13;

if (solovoyStrassen(num1, iter))
    document.write(num1 + " is prime"+ "</br>");
else
    document.write(num1 + " is composite" + "</br>");

if (solovoyStrassen(num2,iter))
    document.write(num2 + " is prime"+ "</br>");
else
    document.write(num2 + " is composite"+ "</br>");

</script>

Output :

15 is composite
13 is prime

Running Time: Using fast algorithms for modular exponentiation, the running time of this algorithm is O(k·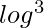n), where k is the number of different values we test.
Auxiliary Space: O(1) as it is using constant space for variables

Accuracy: It is possible for the algorithm to return an incorrect answer. If the input n is indeed prime, then the output will always probably be correctly prime. However, if the input n is composite, then it is possible for the output to probably be incorrect prime. The number n is then called an Euler-Jacobi pseudoprime.
This article is contributed by Palash Nigam . If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.