Count of cyclic permutations having XOR with other binary string as 0
Given two binary strings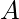 
and 
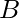. Let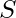 
be set of all the cyclic permutations of string 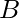. The task is to find how many strings in set 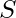when XORed with 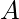give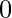 
as result.
Examples:
Input: A = “101”, B = “101”
Output: 1
S = {“101”, “011”, “110”}
Only “101” XOR “101” = 0Input: A = “111”, B = “111”
Output: 3
Approach: Concatenate 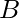with 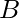so that it contains all of it’s cyclic permutations as sub-strings. Now the problem is reduced to find the number of occurrences of pattern 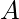in string 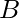which can be solved using Z algorithm (for linear time pattern searching).
Below is the implementation of the above approach:
C++
// C++ program to find bitwise XOR between binary // string A and all the cyclic permutations // of binary string B #include <bits/stdc++.h> using namespace std; // Implementation of Z-algorithm // for linear time pattern searching void compute_z(string s, int z[]) { int l = 0, r = 0; int n = s.length(); for (int i = 1; i <= n - 1; i++) { if (i > r) { l = i, r = i; while (r < n && s[r - l] == s[r]) r++; z[i] = r - l; r--; } else { int k = i - l; if (z[k] < r - i + 1) { z[i] = z[k]; } else { l = i; while (r < n && s[r - l] == s[r]) r++; z[i] = r - l; r--; } } } } // Function to get the count of the cyclic // permutations of b that given 0 when XORed with a int countPermutation(string a, string b) { // concatenate b with b b = b + b; // new b now contains all the cyclic // permutations of old b as it's sub-strings b = b.substr(0, b.size() - 1); // concatenate pattern with text int ans = 0; string s = a + "$" + b; int n = s.length(); // Fill z array used in Z algorithm int z[n]; compute_z(s, z); for (int i = 1; i <= n - 1; i++) { // pattern occurs at index i since // z value of i equals pattern length if (z[i] == a.length()) ans++; } return ans; } // Driver code int main() { string a = "101"; string b = "101"; cout << countPermutation(a, b) << endl; return 0; } |
Java
// Java program to find bitwise XOR between binary // string A and all the cyclic permutations // of binary string B public class GFG{ // Implementation of Z-algorithm // for linear time pattern searching static void compute_z(String s, int z[]) { int l = 0, r = 0; int n = s.length(); for (int i = 1; i <= n - 1; i++) { if (i > r) { l = i; r = i; while (r < n && s.charAt(r - l) == s.charAt(r)) r++; z[i] = r - l; r--; } else { int k = i - l; if (z[k] < r - i + 1) { z[i] = z[k]; } else { l = i; while (r < n && s.charAt(r - l) == s.charAt(r)) r++; z[i] = r - l; r--; } } } } // Function to get the count of the cyclic // permutations of b that given 0 when XORed with a static int countPermutation(String a, String b) { // concatenate b with b b = b + b; // new b now contains all the cyclic // permutations of old b as it's sub-strings b = b.substring(0, b.length() - 1); // concatenate pattern with text int ans = 0; String s = a + "$" + b; int n = s.length(); // Fill z array used in Z algorithm int z[] = new int[n]; compute_z(s, z); for (int i = 1; i <= n - 1; i++) { // pattern occurs at index i since // z value of i equals pattern length if (z[i] == a.length()) ans++; } return ans; } // Driver Code public static void main(String []args){ String a = "101"; String b = "101"; System.out.println(countPermutation(a, b)) ; } // This code is contributed by ANKITRAI1 } |
Python3
# Python 3 program to find bitwise XOR # between binary string A and all the # cyclic permutations of binary string B # Implementation of Z-algorithm # for linear time pattern searching def compute_z(s, z): l = 0 r = 0 n = len(s) for i in range(1, n, 1): if (i > r): l = i r = i while (r < n and s[r - l] == s[r]): r += 1 z[i] = r - l r -= 1 else: k = i - l if (z[k] < r - i + 1): z[i] = z[k] else: l = i while (r < n and s[r - l] == s[r]): r += 1 z[i] = r - l r -= 1 # Function to get the count of the cyclic # permutations of b that given 0 when XORed with a def countPermutation(a, b): # concatenate b with b b = b + b # new b now contains all the cyclic # permutations of old b as it's sub-strings b = b[0:len(b) - 1] # concatenate pattern with text ans = 0 s = a + "$" + b n = len(s) # Fill z array used in Z algorithm z = [0 for i in range(n)] compute_z(s, z) for i in range(1, n, 1): # pattern occurs at index i since # z value of i equals pattern length if (z[i] == len(a)): ans += 1 return ans # Driver code if __name__ == '__main__': a = "101" b = "101" print(countPermutation(a, b)) # This code is contributed by # Surendra_Gangwar |
C#
// C# program to find bitwise XOR between // binary string A and all the cyclic // permutations of binary string B using System; class GFG { // Implementation of Z-algorithm // for linear time pattern searching public static void compute_z(string s, int[] z) { int l = 0, r = 0; int n = s.Length; for (int i = 1; i <= n - 1; i++) { if (i > r) { l = i; r = i; while (r < n && s[r - l] == s[r]) { r++; } z[i] = r - l; r--; } else { int k = i - l; if (z[k] < r - i + 1) { z[i] = z[k]; } else { l = i; while (r < n && s[r - l] == s[r]) { r++; } z[i] = r - l; r--; } } } } // Function to get the count of the // cyclic permutations of b that // given 0 when XORed with a public static int countPermutation(string a, string b) { // concatenate b with b b = b + b; // new b now contains all the cyclic // permutations of old b as it's sub-strings b = b.Substring(0, b.Length - 1); // concatenate pattern with text int ans = 0; string s = a + "$" + b; int n = s.Length; // Fill z array used in Z algorithm int[] z = new int[n]; compute_z(s, z); for (int i = 1; i <= n - 1; i++) { // pattern occurs at index i since // z value of i equals pattern length if (z[i] == a.Length) { ans++; } } return ans; } // Driver Code public static void Main(string[] args) { string a = "101"; string b = "101"; Console.WriteLine(countPermutation(a, b)); } } // This code is contributed by Shrikant13 |
Output:
1
Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.
