Bit Manipulation for Competitive Programming
Last Updated :
26 Apr, 2024
Bit manipulation is a technique in competitive programming that involves the manipulation of individual bits in binary representations of numbers. It is a valuable technique in competitive programming because it allows you to solve problems efficiently, often reducing time complexity and memory usage.
Bitwise Operators:
Bitwise Operators are used to perform operations on individual bits in binary representations of numbers. Some common bitwise operators that are used in competitive programming:-
- Bitwise AND (&): It is a bitwise operator that takes two numbers as operands and performs logical AND on corresponding bits of two numbers. When both bits in the compared position are 1, the bit in the resulting binary representation is 1, otherwise, the result is 0.
- Bitwise OR (|): This bitwise operator takes two numbers as operands and performs a logical OR operation on their corresponding bits. When at least one of the bits in the compared position is 1, the bit in the resulting binary representation is 1, otherwise, the result is 0.
- Bitwise XOR (^): The bitwise XOR operator also takes two numbers as operands and performs an exclusive OR operation on their corresponding bits. When exactly one of the bits in the compared position is 1, the bit in the resulting binary representation is 1, otherwise, the result is 0.
- Bitwise NOT (~): The bitwise NOT is a unary operator operates on a single number and flips (inverts) all its bits. It changes 0s to 1s and 1s to 0s, effectively creating the one’s complement of the input number.
- Left Shift (<<): The left shift operator takes two operands, the number to be shifted and the number of places to move it to the left. It shifts the bits of the first operand to the left by the number of places specified in the second operand. This is actually multiplying a number by 2 raised to the power of shift counts. For example: 5 << 2 =20, the binary representation of 5 (0101) is shifted left by 2 positions, resulting in 20 (10100) in decimal.
- Right Shift (>>): The right shift operator also takes two operands, the number to be shifted and the number of places to move it to the right. It shifts the bits of the first operand to the right by the number of places specified in the second operand. This is equivalent to dividing a number by 2 raised to the power of the shift count (integer division). For example: 20 >> 2 = 5, where the binary representation of 20 (10100) is shifted right by 2 positions, resulting in 5 (00101) in decimal.
Useful Bitwise Tricks for Competitive Programming:
This can be done by left-shifting the value 1 by ‘pos‘ positions (1<< pos) and performing a bitwise OR operation with number n. This operation effectively turns on the bit at the specified position.
C++
// n=number
// pos=It is the position at which we want to set the bit
void set(int & n, int pos)
{
n |= (1 << pos);
}
public class GFG {
// Function to set a bit at a given position
// in a number
static int setBit(int n, int pos)
{
return n | (1 << pos);
}
}
# n = number
# pos = It is the position at which we want to set the bit
def set_bit(n, pos):
n |= (1 << pos)
// Function to set a bit at the specified position in an
// integer n: reference to the number pos: the position at
// which the bit should be set
static void Set(ref int n, int pos)
{
// Use bitwise left shift (1 << pos) to create a mask
// with a 1 at the specified position Use bitwise OR
// assignment (|=) to set the bit at the specified
// position in the number
n |= (1 << pos);
}
// n = number
// pos = It is the position at which we want to set the bit
function set(n, pos) {
n |= (1 << pos);
}
//this code is contributed by Adarsh
This can be done by left-shifting the value 1 by pos positions (1<< pos) and then use bitwise NOT operator ‘~’ to unset this shifted 1, making the bit at position pos to 0 and then use Bitwise AND with the number n that will unset bit at desired positoon of number n.
C++
// Unset (clear) a bit at position pos in number n
void unset(int &n, int pos) {
return ( n &= ~(1 << pos));
}
// Unset (clear) a bit at position pos in number n
void unset(int[] n, int pos) {
return (n &= ~(1 << pos));
}
# Unset (clear) a bit at position pos in number n
def unset_bit(n, pos):
return( n &= ~(1 << pos))
Use the bitwise XOR (^) operator to toggle (flip) the bit at the given position. If the bit is 0, it becomes 1, and if it’s 1, it becomes 0.
C++
// Flip (toggle) a bit at position pos in number n
void flip(int &n, int pos) {
n ^= (1 << pos);
}
# Flip (toggle) a bit at position pos in number n
def flip_bit(n, pos):
n ^= (1 << pos)
This can be done by performing a bitwise AND operation with a mask having only that bit set. If the result is non-zero, the bit is set; otherwise, it’s unset.
C++
// Check if the bit at position pos in number n is set (1) or unset (0)
bool isBitSet(int n, int pos) {
return ((n & (1 << pos)) != 0);
}
# Check if the bit at position pos in number n is set (1) or unset (0)
def is_bit_set(n, pos):
return (n & (1 << pos)) != 0
A power of two is a number with only one bit set in its binary representation, while the number just before it has that bit unset and all the following bits set. Consequently, when you perform a bitwise AND operation between a number and its predecessor, the result will always be 0.
C++
// Check if n is a power of two
bool isPowerOfTwo(int n) {
return ((n & (n - 1)) == 0);
}
# Check if n is a power of two
def is_power_of_two(n):
return (n & (n - 1)) == 0
Prefix Sum and Bit Manipulation Technique:
Suppose you are given an array a of n numbers and q queries and each query is of the form (l,r). The task is to compute Bitwise AND of the numbers from index l to r i.e., (al & al+1 ….. & ar-1 & ar).
A simple approach will be for each query travese from index l to r and compute Bitwise AND. By this we will be able to answer each query in O(n) time in worst case.
But to answer each query in constant time prefix sum can be a useful method.
1. How to compute Bitwise AND for a range using Prefix Sum Technique:
- Storing Bit Information: To start, we want to determine whether a specific bit (let’s call it the “j-th bit”) in the binary representation of a number at a given index (let’s call it “i”) is set (1) or unset (0). We accomplish this by creating a 2D array called “temp,” with dimensions “n x 32” (assuming 32-bit integers), where “n” is the number of elements in our array. Each cell “temp[i][j]” stores this information for the i-th number’s j-th bit.
- Computing Prefix Sums: Next, we calculate prefix sums for each bit position (from 0 to 31, assuming 32-bit integers) in our “temp” array. This “prefix sum” array, let’s call it “psum,” keeps track of the count of numbers up to a certain index that have their j-th bit set.
- Determining the Bitwise AND for a Range: Now, let’s focus on finding the Bitwise AND of numbers within a specific range, say from index “l” to “r.” To determine whether the j-th bit of the result should be set to 1, we compare the number of elements with the j-th bit set in the range [l, r]. This can be done using prefix sum array psum. psum[i][j] will denote numbers of elements till index i, which have their jth bit set and
psum[r][j]-psum[l-1][j] will give number of indexes from l to r which have their jth bit set. - Setting the Result Bit: If the count of numbers with the j-th bit set in the range [l, r] is equal to the range size (r – l + 1), it means that all numbers in that range have their j-th bit set. In this case, we set the j-th bit of the result to 1. Otherwise, if not all numbers in the range have the j-th bit set, we set it to 0.
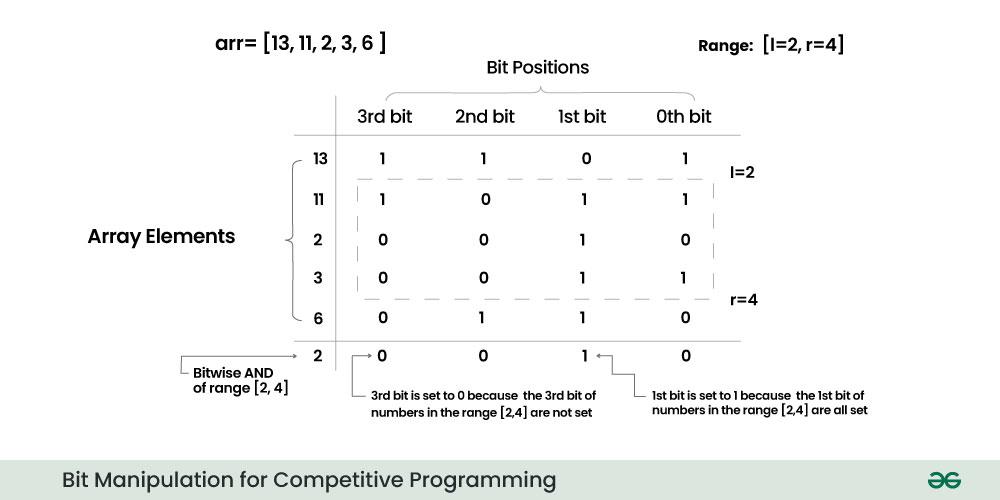
Bit Manipulation for Competitive Programming
Below is the code for above approach:
C++
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> prefixsumBit(vector<int>& nums) {
int n = nums.size();
// Step 1: Store bit information in 'temp'
vector<vector<int>> temp(n + 1, vector<int>(32, 0));
for (int i = 1; i <= n; ++i) {
int num = nums[i - 1]; // Fix indexing error
for (int j = 0; j < 32; ++j) {
// Check if the j-th bit of nums[i] is set
if (((1 << j) & num) != 0) { // Fix indexing error
temp[i][j] = 1;
}
}
}
// Step 2: Compute prefix sums
vector<vector<int>> psum(n + 1, vector<int>(32, 0));
for (int j = 0; j < 32; ++j) {
for (int i = 1; i <= n; ++i) {
// Calculate prefix sum for each bit
psum[i][j] = psum[i - 1][j] + temp[i][j];
}
}
return psum;
}
int rangeBitwiseAND(vector<vector<int>>& psum, int l, int r) {
int result = 0;
for (int j = 0; j < 32; ++j) {
// Calculate the count of elements with j-th bit set
// in the range [l, r]
int count = psum[r][j] - psum[l - 1][j];
if (count == r - l + 1) {
// If all elements in the range have j-th bit
// set, add it to the result
result = result + (1 << j);
}
}
return result;
}
// driver's code
int main() {
// Input Array
vector<int> nums = { 13, 11, 2, 3, 6 };
// Range
int l = 2, r = 4;
// 2D prefix sum
vector<vector<int>> psum = prefixsumBit(nums);
cout << "Bitwise AND of range [2,4] is: " << rangeBitwiseAND(psum, l, r);
return 0;
}
// Java program for the above approach
import java.util.*;
public class GFG {
public static List<List<Integer> >
prefixsumBit(List<Integer> nums)
{
int n = nums.size();
// Step 1: Store bit information in 'temp'
List<List<Integer> > temp = new ArrayList<>();
for (int i = 0; i <= n; ++i) {
temp.add(new ArrayList<>(
Collections.nCopies(32, 0)));
}
for (int i = 1; i <= n; ++i) {
int num = nums.get(i - 1);
for (int j = 0; j < 32; ++j) {
// Check if the j-th bit of nums[i] is set
if (((1 << j) & num) != 0) {
temp.get(i).set(j, 1);
}
}
}
// Step 2: Compute prefix sums
List<List<Integer> > psum = new ArrayList<>();
for (int i = 0; i <= n; ++i) {
psum.add(new ArrayList<>(
Collections.nCopies(32, 0)));
}
for (int j = 0; j < 32; ++j) {
for (int i = 1; i <= n; ++i) {
// Calculate prefix sum for each bit
psum.get(i).set(j,
psum.get(i - 1).get(j)
+ temp.get(i).get(j));
}
}
return psum;
}
public static int
rangeBitwiseAND(List<List<Integer> > psum, int l, int r)
{
int result = 0;
for (int j = 0; j < 32; ++j) {
// Calculate the count of elements with j-th bit
// set in the range [l, r]
int count = psum.get(r).get(j)
- psum.get(l - 1).get(j);
if (count == r - l + 1) {
// If all elements in the range have j-th
// bit set, add it to the result
result = result + (1 << j);
}
}
return result;
}
public static void main(String[] args)
{
// Input Array
List<Integer> nums = new ArrayList<>(
Arrays.asList(13, 11, 2, 3, 6));
// Range
int l = 2, r = 4;
// 2D prefix sum
List<List<Integer> > psum = prefixsumBit(nums);
System.out.println(
"Bitwise AND of range [2,4] is : "
+ rangeBitwiseAND(psum, l, r));
}
}
// This code is contributed by Susobhan Akhuli
def prefixsumBit(nums):
n = len(nums)
temp = [[0] * 32 for _ in range(n + 1)]
# Step 1: Store bit information in 'temp'
for i in range(1, n + 1):
num = nums[i - 1]
for j in range(32):
# Check if the j-th bit of nums[i] is set
if ((1 << j) & num) != 0:
temp[i][j] = 1
# Step 2: Compute prefix sums
psum = [[0] * 32 for _ in range(n + 1)]
for j in range(32):
for i in range(1, n + 1):
# Calculate prefix sum for each bit
psum[i][j] = psum[i - 1][j] + temp[i][j]
return psum
def rangeBitwiseAND(psum, l, r):
result = 0
for j in range(32):
# Calculate the count of elements with j-th bit set
# in the range [l, r]
count = psum[r][j] - psum[l - 1][j]
if count == r - l + 1:
# If all elements in the range have j-th bit
# set, add it to the result
result += (1 << j)
return result
# driver's code
if __name__ == "__main__":
# Input Array
nums = [13, 11, 2, 3, 6]
# Range
l, r = 2, 4
# 2D prefix sum
psum = prefixsumBit(nums)
print("Bitwise AND of range [2,4] is:", rangeBitwiseAND(psum, l, r))
function GFG(nums) {
const n = nums.length;
// Step 1: Store bit information in 'temp'
const temp = new Array(n + 1).fill(0).map(() => new Array(32).fill(0));
for (let i = 1; i <= n; ++i) {
let num = nums[i - 1];
for (let j = 0; j < 32; ++j) {
// Check if the j-th bit of the nums[i] is set
if (((1 << j) & num) !== 0) {
temp[i][j] = 1;
}
}
}
// Step 2: Compute prefix sums
const psum = new Array(n + 1).fill(0).map(() => new Array(32).fill(0));
for (let j = 0; j < 32; ++j) {
for (let i = 1; i <= n; ++i) {
// Calculate prefix sum for the each bit
psum[i][j] = psum[i - 1][j] + temp[i][j];
}
}
return psum;
}
// Function to compute bitwise AND of range [l, r]
function rangeBitwiseAND(psum, l, r) {
let result = 0;
for (let j = 0; j < 32; ++j) {
// Calculate the count of elements with j-th bit set
// in the range [l, r]
const count = psum[r][j] - psum[l - 1][j];
if (count === r - l + 1) {
result += (1 << j);
}
}
return result;
}
// Main function
function main() {
// Input Array
const nums = [13, 11, 2, 3, 6];
const l = 2, r = 4;
const psum = GFG(nums);
console.log(`Bitwise AND of range [${l},${r}] is : ${rangeBitwiseAND(psum, l, r)}`);
}
// Invoke main function
main();
OutputBitwise AND of range [2,4] is: 2
Note- When you increase the range for Bitwise AND, the result will never increase; it will either stay the same or decrease. This is a useful property and we can apply Binary search on answer we are given to determine the largest range whose Bitwise AND is greater than or equal to a given number.
2. Determining the Bitwise OR for a Range:
Bitwise OR can be computed in a similar way. WE will make temp and psum array in a similar way,
- To determine whether the j-th bit of the result should be set to 1, we compare the number of elements with the j-th bit set in the range [l, r].
- Use the prefix sum array, psum, we can get count of numbers with the jth bit set in range [l,r] from psum[r][j]-psum[l-1][j].
- If the count of numbers with the j-th bit set in the range [l, r] is greater than 0, it means at least one number in that range has the j-th bit set. In this case, we set the j-th bit of the result to 1. Otherwise, if no numbers in the range have the j-th bit set, we set it to 0.
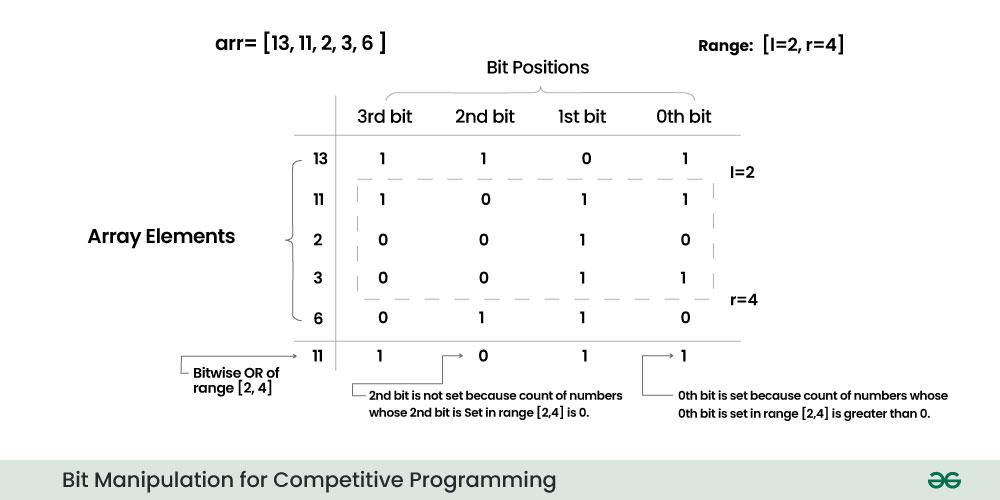
Bit Manipulation for Competitive Programming
Below is the code for above approach:
C++
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> prefixsumBit(vector<int>& nums) {
int n = nums.size();
vector<vector<int>> temp(n + 1, vector<int>(32, 0));
// Step 1: Store bit information in 'temp'
for (int i = 1; i <= n; ++i) {
int num = nums[i - 1];
for (int j = 0; j < 32; ++j) {
// Check if the j-th bit of nums[i] is set
if ((1 << j) & num) {
temp[i][j] = 1;
}
}
}
// Step 2: Compute prefix sums
vector<vector<int>> psum(n + 1, vector<int>(32, 0));
for (int j = 0; j < 32; ++j) {
for (int i = 1; i <= n; ++i) {
// Calculate prefix sum for each bit
psum[i][j] = psum[i - 1][j] + temp[i][j];
}
}
return psum;
}
int rangeBitwiseOR(vector<vector<int>>& psum, int l, int r) {
int result = 0;
for (int j = 0; j < 32; ++j) {
// Calculate the count of elements with j-th bit set
// in the range [l, r]
int count = psum[r][j] - psum[l - 1][j];
// If at least one element in the range has j-th bit
// set, add it to the result
if (count > 0) {
result += (1 << j);
}
}
return result;
}
// Driver's code
int main() {
// Input Array
vector<int> nums = {13, 11, 2, 3, 6};
// Range
int l = 2, r = 4;
// 2D prefix sum
vector<vector<int>> psum = prefixsumBit(nums);
cout << "Bitwise OR of range [2,4] is: " << rangeBitwiseOR(psum, l, r) << endl;
return 0;
}
import java.util.*;
public class Main {
public static int[][] prefixsumBit(int[] nums) {
int n = nums.length;
int[][] temp = new int[n + 1][32];
// Step 1: Store bit information in 'temp'
for (int i = 1; i <= n; ++i) {
int num = nums[i - 1];
for (int j = 0; j < 32; ++j) {
// Check if the j-th bit of nums[i] is set
if (((1 << j) & num) != 0) {
temp[i][j] = 1;
}
}
}
// Step 2: Compute prefix sums
int[][] psum = new int[n + 1][32];
for (int j = 0; j < 32; ++j) {
for (int i = 1; i <= n; ++i) {
// Calculate prefix sum for each bit
psum[i][j] = psum[i - 1][j] + temp[i][j];
}
}
return psum;
}
public static int rangeBitwiseOR(int[][] psum, int l, int r) {
int result = 0;
for (int j = 0; j < 32; ++j) {
// Calculate the count of elements with j-th bit set
// in the range [l, r]
int count = psum[r][j] - psum[l - 1][j];
// If at least one element in the range has j-th bit
// set, add it to the result
if (count > 0) {
result += (1 << j);
}
}
return result;
}
public static void main(String[] args) {
// Input Array
int[] nums = {13, 11, 2, 3, 6};
// Range
int l = 2, r = 4;
// 2D prefix sum
int[][] psum = prefixsumBit(nums);
System.out.println("Bitwise OR of range [2,4] is: " + rangeBitwiseOR(psum, l, r));
}
}
def prefixsumBit(nums):
n = len(nums)
temp = [[0] * 32 for _ in range(n + 1)]
# Step 1: Store bit information in 'temp'
for i in range(1, n + 1):
num = nums[i - 1]
for j in range(32):
# Check if the j-th bit of nums[i] is set
if (1 << j) & num:
temp[i][j] = 1
# Step 2: Compute prefix sums
psum = [[0] * 32 for _ in range(n + 1)]
for j in range(32):
for i in range(1, n + 1):
# Calculate prefix sum for each bit
psum[i][j] = psum[i - 1][j] + temp[i][j]
return psum
def rangeBitwiseOR(psum, l, r):
result = 0
for j in range(32):
# Calculate the count of elements with j-th bit set
# in the range [l, r]
count = psum[r][j] - psum[l - 1][j]
# If at least one element in the range has j-th bit
# set, add it to the result
if count > 0:
result += (1 << j)
return result
# Driver's code
if __name__ == "__main__":
# Input Array
nums = [13, 11, 2, 3, 6]
# Range
l, r = 2, 4
# 2D prefix sum
psum = prefixsumBit(nums)
print("Bitwise OR of range [2,4] is:", rangeBitwiseOR(psum, l, r))
using System;
using System.Collections.Generic;
class Program
{
static List<List<int>> PrefixSumBit(List<int> nums)
{
int n = nums.Count;
// Store bit information in 'temp'
List<List<int>> temp = new List<List<int>>(n + 1);
for (int i = 0; i <= n; ++i)
{
temp.Add(new List<int>(32));
for (int j = 0; j < 32; ++j)
{
temp[i].Add(0);
}
}
for (int i = 1; i <= n; ++i)
{
int num = nums[i - 1];
for (int j = 0; j < 32; ++j)
{
// Check if the j-th bit of nums[i] is set
if (((1 << j) & num) != 0)
{
temp[i][j] = 1;
}
}
}
// Compute prefix sums
List<List<int>> psum = new List<List<int>>(n + 1);
for (int i = 0; i <= n; ++i)
{
psum.Add(new List<int>(32));
for (int j = 0; j < 32; ++j)
{
psum[i].Add(0);
}
}
for (int j = 0; j < 32; ++j)
{
for (int i = 1; i <= n; ++i)
{
// Calculate prefix sum for each bit
psum[i][j] = psum[i - 1][j] + temp[i][j];
}
}
return psum;
}
static int RangeBitwiseOR(List<List<int>> psum, int l, int r)
{
int result = 0;
for (int j = 0; j < 32; ++j)
{
// Calculate the count of elements with j-th bit set
// in the range [l, r]
int count = psum[r][j] - psum[l - 1][j];
// If at least one element in the range has j-th bit
// set, add it to the result
if (count > 0)
{
result = result + (1 << j);
}
}
return result;
}
// driver's code
static void Main()
{
// Input Array
List<int> nums = new List<int> { 13, 11, 2, 3, 6 };
// Range
int l = 2, r = 4;
// 2D prefix sum
List<List<int>> psum = PrefixSumBit(nums);
Console.WriteLine($"Bitwise OR of range [2,4] is : {RangeBitwiseOR(psum, l, r)}");
}
}
function prefixSumBit(nums) {
const n = nums.length;
// Step 1: Store bit information in 'temp'
const temp = Array.from({ length: n + 1 }, () => Array(32).fill(0));
for (let i = 1; i <= n; ++i) {
const num = nums[i - 1];
for (let j = 0; j < 32; ++j) {
// Check if the j-th bit of nums[i] is set
if (((1 << j) & num) !== 0) {
temp[i][j] = 1;
}
}
}
// Step 2: Compute prefix sums
const psum = Array.from({ length: n + 1 }, () => Array(32).fill(0));
for (let j = 0; j < 32; ++j) {
for (let i = 1; i <= n; ++i) {
// Calculate prefix sum for each bit
psum[i][j] = psum[i - 1][j] + temp[i][j];
}
}
return psum;
}
function rangeBitwiseOR(psum, l, r) {
let result = 0;
for (let j = 0; j < 32; ++j) {
// Calculate the count of elements with j-th bit set
// in the range [l, r]
const count = psum[r][j] - psum[l - 1][j];
// If at least one element in the range has j-th bit
// set, add it to the result
if (count > 0) {
result = result + (1 << j);
}
}
return result;
}
// Driver's code
function main() {
// Input Array
const nums = [13, 11, 2, 3, 6];
// Range
const l = 2, r = 4;
// 2D prefix sum
const psum = prefixSumBit(nums);
console.log("Bitwise OR of range [2,4] is:", rangeBitwiseOR(psum, l, r));
}
// Call the main function
main();
OutputBitwise OR of range [2,4] is: 11
Note: When you increase the range for Bitwise OR, the result will never decrease; it will either stay the same or increase. Again this is a useful property and we can apply Binary search on answer we are given to determine the smallest range whose Bitwise OR is smaller than or equal to a given number.
3. Determining the Bitwise XOR for a Range:
Bitwise XOR for a range can be done in similar way:
- To determine whether the j-th bit of the result should be set to 1, we compare the number of elements with the j-th bit set in the range [l, r].
- Use the prefix sum array, psum, we can get count of numbers with the jth bit set in range [l,r] from psum[r][j]-psum[l-1][j].
- If the count of numbers with the j-th bit set in the range [l, r] is odd, it means that the j-th bit of the result should be set to 1. If the count is even, the j-th bit of the result should be set to 0.
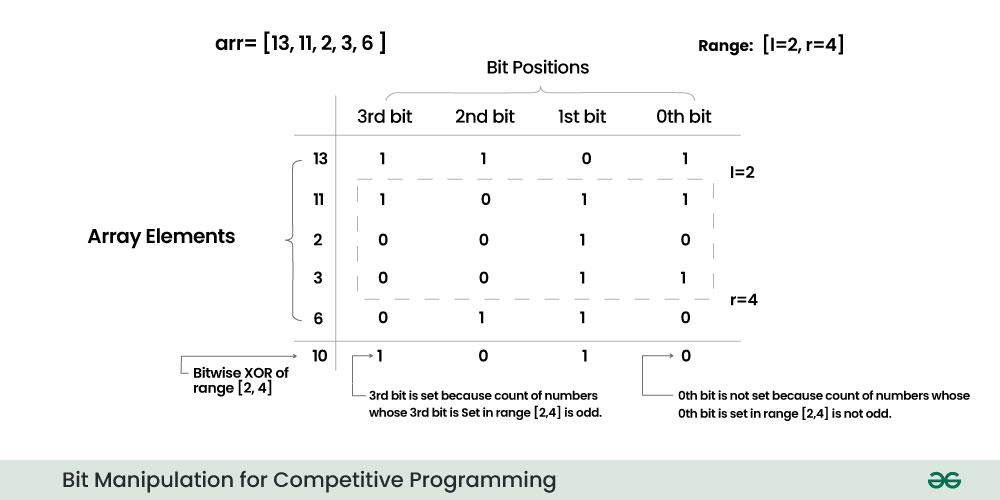
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> prefixsumBit(vector<int>& nums)
{
int n = nums.size();
// Step 1: Store bit information in 'temp'
vector<vector<int>> temp(n + 1, vector<int>(32, 0));
for (int i = 1; i <= n; ++i) { // Fixed indexing
int num = nums[i - 1]; // Fixed indexing
for (int j = 0; j < 32; ++j) {
// Check if the j-th bit of nums[i] is set
if (((1 << j) & num) != 0) { // Fixed indexing
temp[i][j] = 1;
}
}
}
// Step 2: Compute prefix sums
vector<vector<int>> psum(n + 1, vector<int>(32, 0));
for (int j = 0; j < 32; ++j) {
for (int i = 1; i <= n; ++i) {
// Calculate prefix sum for each bit
psum[i][j] = psum[i - 1][j] + temp[i][j];
}
}
return psum;
}
int rangeBitwiseXOR(vector<vector<int>>& psum, int l,
int r)
{
int result = 0;
for (int j = 0; j < 32; ++j) {
// Calculate the count of elements with j-th bit set
// in the range [l, r]
int count = psum[r][j] - psum[l - 1][j];
// If count is odd, add it to the result
if (count % 2 == 1) {
result = result + (1 << j);
}
}
return result;
}
// driver's code
int main()
{
// Input Array
vector<int> nums = { 13, 11, 2, 3, 6 };
// Range
int l = 2, r = 4;
// 2D prefix sum
vector<vector<int>> psum = prefixsumBit(nums);
cout << "Bitwise XOR of range [2,4] is :" << rangeBitwiseXOR(psum, l, r);
return 0;
}
// Java Code
public class PrefixSumBit {
// Function to compute the prefix sum of bits for each element in nums
public static int[][] prefixSumBit(int[] nums) {
int n = nums.length;
int[][] temp = new int[n + 1][32];
// Step 1: Store bit information in 'temp'
for (int i = 1; i <= n; i++) {
int num = nums[i - 1];
for (int j = 0; j < 32; j++) {
// Check if the j-th bit of nums[i] is set
if ((1 << j & num) != 0) {
temp[i][j] = 1;
}
}
}
// Step 2: Compute prefix sums
int[][] psum = new int[n + 1][32];
for (int j = 0; j < 32; j++) {
for (int i = 1; i <= n; i++) {
// Calculate prefix sum for each bit
psum[i][j] = psum[i - 1][j] + temp[i][j];
}
}
return psum;
}
// Function to calculate bitwise XOR of range [l, r]
public static int rangeBitwiseXOR(int[][] psum, int l, int r) {
int result = 0;
for (int j = 0; j < 32; j++) {
// Calculate the count of elements with j-th bit set
// in the range [l, r]
int count = psum[r][j] - psum[l - 1][j];
// If count is odd, add it to the result
if (count % 2 == 1) {
result += (1 << j);
}
}
return result;
}
// Driver's code
public static void main(String[] args) {
// Input Array
int[] nums = {13, 11, 2, 3, 6};
// Range
int l = 2, r = 4;
// 2D prefix sum
int[][] psum = prefixSumBit(nums);
System.out.println("Bitwise XOR of range [2,4] is: " + rangeBitwiseXOR(psum, l, r));
}
}
// This Code is contributed by guptapratik
def prefixsumBit(nums):
n = len(nums)
temp = [[0] * 32 for _ in range(n + 1)]
# Step 1: Store bit information in 'temp'
for i in range(1, n + 1):
num = nums[i - 1]
for j in range(32):
# Check if the j-th bit of nums[i] is set
if (1 << j) & num:
temp[i][j] = 1
# Step 2: Compute prefix sums
psum = [[0] * 32 for _ in range(n + 1)]
for j in range(32):
for i in range(1, n + 1):
# Calculate prefix sum for each bit
psum[i][j] = psum[i - 1][j] + temp[i][j]
return psum
def rangeBitwiseXOR(psum, l, r):
result = 0
for j in range(32):
# Calculate the count of elements with j-th bit set
# in the range [l, r]
count = psum[r][j] - psum[l - 1][j]
# If count is odd, add it to the result
if count % 2 == 1:
result += (1 << j)
return result
# Driver's code
if __name__ == "__main__":
# Input Array
nums = [13, 11, 2, 3, 6]
# Range
l, r = 2, 4
# 2D prefix sum
psum = prefixsumBit(nums)
print("Bitwise XOR of range [2,4] is:", rangeBitwiseXOR(psum, l, r))
// C# program for the above approach
using System;
using System.Collections.Generic;
public class GFG {
// Function to compute the prefix sum of each bit in the
// given array
static List<List<int> > PrefixSumBit(List<int> nums)
{
int n = nums.Count;
// Step 1: Store bit information in 'temp'
List<List<int> > temp = new List<List<int> >();
for (int i = 0; i <= n; ++i) {
temp.Add(new List<int>(
new int[32])); // Initialize with 32 zeros
if (i > 0) {
int num = nums[i - 1];
for (int j = 0; j < 32; ++j) {
// Check if the j-th bit of nums[i] is
// set
if (((1 << j) & num) != 0) {
temp[i][j] = 1;
}
}
}
}
// Step 2: Compute prefix sums
List<List<int> > psum = new List<List<int> >();
for (int i = 0; i <= n; ++i) {
psum.Add(new List<int>(
new int[32])); // Initialize with 32 zeros
}
for (int j = 0; j < 32; ++j) {
for (int i = 1; i <= n; ++i) {
// Calculate prefix sum for each bit
psum[i][j] = psum[i - 1][j] + temp[i][j];
}
}
return psum;
}
// Function to compute the bitwise XOR of the range [l,
// r]
static int RangeBitwiseXOR(List<List<int> > psum, int l,
int r)
{
int result = 0;
for (int j = 0; j < 32; ++j) {
// Calculate the count of elements with j-th bit
// set in the range [l, r]
int count = psum[r][j] - psum[l - 1][j];
// If count is odd, add it to the result
if (count % 2 == 1) {
result = result + (1 << j);
}
}
return result;
}
// Main method
public static void Main(string[] args)
{
// Input Array
List<int> nums = new List<int>{ 13, 11, 2, 3, 6 };
// Range
int l = 2, r = 4;
// 2D prefix sum
List<List<int> > psum = PrefixSumBit(nums);
Console.WriteLine("Bitwise XOR of range [2,4] is: "
+ RangeBitwiseXOR(psum, l, r));
}
}
// This code is contributed by Susobhan Akhuli
// Function to compute the prefix sum of bits for each element in nums
function prefixSumBit(nums) {
let n = nums.length;
let temp = new Array(n + 1).fill(null).map(() => new Array(32).fill(0));
// Step 1: Store bit information in 'temp'
for (let i = 1; i <= n; i++) {
let num = nums[i - 1];
for (let j = 0; j < 32; j++) {
// Check if the j-th bit of nums[i] is set
if ((1 << j & num) !== 0) {
temp[i][j] = 1;
}
}
}
// Step 2: Compute prefix sums
let psum = new Array(n + 1).fill(null).map(() => new Array(32).fill(0));
for (let j = 0; j < 32; j++) {
for (let i = 1; i <= n; i++) {
// Calculate prefix sum for each bit
psum[i][j] = psum[i - 1][j] + temp[i][j];
}
}
return psum;
}
// Function to calculate bitwise XOR of range [l, r]
function rangeBitwiseXOR(psum, l, r) {
let result = 0;
for (let j = 0; j < 32; j++) {
// Calculate the count of elements with j-th bit set
// in the range [l, r]
let count = psum[r][j] - psum[l - 1][j];
// If count is odd, add it to the result
if (count % 2 === 1) {
result += (1 << j);
}
}
return result;
}
// Driver's code
function main() {
// Input Array
let nums = [13, 11, 2, 3, 6];
// Range
let l = 2, r = 4;
// 2D prefix sum
let psum = prefixSumBit(nums);
console.log("Bitwise XOR of range [2,4] is: " + rangeBitwiseXOR(psum, l, r));
}
// Calling the main function
main();
OutputBitwise XOR of range [2,4] is :10
Useful Bitwise Equations:
a|b = a⊕b + a&b
a⊕(a&b) = (a|b)⊕b
(a&b)⊕(a|b) = a⊕b
a+b = a|b + a&b
a+b = a⊕b + 2(a&b)
How to solve Bit Manipulation Problems?
In most of the problems involving bit manipulation it is better to work bit by bit i.e., break down the problem into individual bits. Focus on solving the problem for a single bit position before moving on to the next.
Let’s consider few examples:
Example 1: Given an integer array arr. The task is to find the size of largest subset such that bitwise AND of all the elements of the subset is greater than 0.
Solution:
- Bitwise AND Insight: To start, notice that for a subset’s bitwise AND to be greater than zero, there must be a bit position where all the elements in the subset have that bit set to 1.
- Bit by Bit Exploration: We approach this problem bit by bit, examining each of the 32 possible bit positions in the numbers.
- Counting Ones: For each bit position, we count how many elements in the array have that bit set to 1.
- Finding the Maximum: Our answer is the largest count of elements that have their bit set for a particular bit position.
Example 2: Given an integer array arr of size n. A graph is formed using these elements. There exists an edge between index i and index j if i!=j and a[i] AND a[j]>0. The task is to determine whether there exists a cycle in the graph.
Solution:
Bitwise Analysis: We begin by analyzing each bit position in the binary representation of the numbers and for each bit determine how many elements have that bit set.
- Cycle Detection: For a specific bit position,
- If there are more than two elements in the array that have that bit set, it indicates that there exists a cycle in the graph.
- Otherwise, there will be almost 2 numbers that have a particular bit set. It follows that each bit can contribute to atmost 1 edge.
- Graph Constraints: Importantly, the entire graph won’t have more than 32 edges because each number in the array is represented using 32 bits.
- Cycle Detection Algorithm: To ascertain the presence of a cycle in the graph,a straightforward Depth-First Search (DFS) algorithm can be used.
Practice Problems on Bit Manipulation:
Easy Level Problems on Bit Manipulation:
Medium Level Problems on Bit Manipulation:
Hard Level Problems on Bit Manipulation:
Share your thoughts in the comments
Please Login to comment...