Find interior angles for each side of a given Cyclic Quadrilateral
Last Updated :
21 Apr, 2021
Given four positive integers A, B, C, and D representing the sides of a Cyclic Quadrilateral, the task is to find all the interior angles of the cyclic quadrilateral.
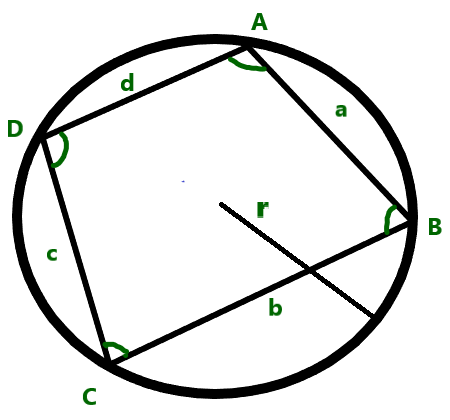
A cyclic quadrilateral is a quadrilateral whose vertices lie on a single circle.
This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic(A, B, C, and D).
( In the figure, r is the circumradius and a, b, c, and d are length of AB, BC, CD, and DA respectively).
Examples:
Input: A = 10, B = 15, C = 20, D = 25
Output:
?A: 85.59 degrees
?B: 122.58 degrees
?C: 94.41 degrees
?D: 57.42 degrees
Input: A = 10, B = 10, C = 10, D = 10
Output:
?A: 90.00 degrees
?B: 90.00 degrees
?C: 90.00 degrees
?D: 90.00 degrees
Approach: The given problem can be solved by using the formula to calculate the cosine of the interior angle of a cyclic quadrilateral. The formula is given by:

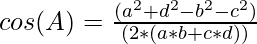
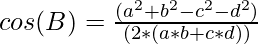
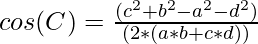
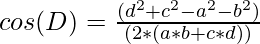
Follow the steps below to solve the problem:
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void findAngles(double a, double b,
double c, double d)
{
double numerator = a * a + d * d
- b * b - c * c;
double denominator = 2 * (a * b + c * d);
double x = numerator / denominator;
cout << fixed << setprecision(2)
<< "A: " << (acos(x) * 180) / 3.141592
<< " degrees";
numerator = a * a + b * b
- c * c - d * d;
x = numerator / denominator;
cout << fixed << setprecision(2)
<< "\nB: " << (acos(x) * 180) / 3.141592
<< " degrees";
numerator = c * c + b * b
- a * a - d * d;
x = numerator / denominator;
cout << fixed << setprecision(2)
<< "\nC: " << (acos(x) * 180) / 3.141592
<< " degrees";
numerator = d * d + c * c
- a * a - b * b;
x = numerator / denominator;
cout << fixed << setprecision(2)
<< "\nD: " << (acos(x) * 180) / 3.141592
<< " degrees";
}
int main()
{
double A = 10, B = 15, C = 20, D = 25;
findAngles(A, B, C, D);
return 0;
}
|
Java
class GFG{
static void findAngles(double a, double b,
double c, double d)
{
double numerator = a * a + d * d -
b * b - c * c;
double denominator = 2 * (a * b + c * d);
double x = numerator / denominator;
System.out.println("A: " +
Math.round(((Math.acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
numerator = a * a + b * b - c * c - d * d;
x = numerator / denominator;
System.out.println("B: " +
Math.round(((Math.acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
numerator = c * c + b * b -
a * a - d * d;
x = numerator / denominator;
System.out.println("C: " +
Math.round(((Math.acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
numerator = d * d + c * c -
a * a - b * b;
x = numerator / denominator;
System.out.println("D: " +
Math.round(((Math.acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
}
public static void main (String[] args)
{
double A = 10, B = 15, C = 20, D = 25;
findAngles(A, B, C, D);
}
}
|
Python3
import math
def findAngles(a, b, c, d):
numerator = a * a + d * d - b * b - c * c
denominator = 2 * (a * b + c * d)
x = numerator / denominator
print("A: ", '%.2f' % ((math.acos(x) * 180) /
3.141592), " degrees")
numerator = a * a + b * b - c * c - d * d
x = numerator / denominator
print("B: ", '%.2f' % ((math.acos(x) * 180) /
3.141592), " degrees")
numerator = c * c + b * b - a * a - d * d
x = numerator / denominator
print("C: ", '%.2f' % ((math.acos(x) * 180) /
3.141592), " degrees")
numerator = d * d + c * c - a * a - b * b
x = numerator / denominator
print("D: ", '%.2f' % ((math.acos(x) * 180) /
3.141592), " degrees")
if __name__ == "__main__":
A = 10
B = 15
C = 20
D = 25
findAngles(A, B, C, D)
|
C#
using System;
class GFG{
static void findAngles(double a, double b,
double c, double d)
{
double numerator = a * a + d * d -
b * b - c * c;
double denominator = 2 * (a * b + c * d);
double x = numerator / denominator;
Console.WriteLine("A: " +
Math.Round(((Math.Acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
numerator = a * a + b * b - c * c - d * d;
x = numerator / denominator;
Console.WriteLine("B: " +
Math.Round(((Math.Acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
numerator = c * c + b * b -
a * a - d * d;
x = numerator / denominator;
Console.WriteLine("C: " +
Math.Round(((Math.Acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
numerator = d * d + c * c -
a * a - b * b;
x = numerator / denominator;
Console.WriteLine("D: " +
Math.Round(((Math.Acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
}
public static void Main(string[] args)
{
double A = 10, B = 15, C = 20, D = 25;
findAngles(A, B, C, D);
}
}
|
Javascript
<script>
function findAngles(a, b, c, d){
var numerator = a * a + d * d - b * b - c * c
var denominator = 2 * (a * b + c * d)
var x = numerator / denominator
document.write("A: ", Math.round(((Math.acos(x) * 180) /
3.141592) * 100) / 100.0, " degrees");
document.write("<br>");
numerator = a * a + b * b - c * c - d * d
x = numerator / denominator
document.write("B: ", Math.round(((Math.acos(x) * 180) /
3.141592) * 100) / 100.0, " degrees");
document.write("<br>");
numerator = c * c + b * b - a * a - d * d
x = numerator / denominator
document.write("C: ", Math.round(((Math.acos(x) * 180) /
3.141592) * 100) / 100.0, " degrees");
document.write("<br>");
numerator = d * d + c * c - a * a - b * b
x = numerator / denominator
document.write("D: ", Math.round(((Math.acos(x) * 180) /
3.141592) * 100) / 100.0, " degrees");
}
var A = 10
var B = 15
var C = 20
var D = 25
findAngles(A, B, C, D)
</script>
|
Output: A: 85.59 degrees
B: 122.58 degrees
C: 94.41 degrees
D: 57.42 degrees
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...