ML | Expectation-Maximization Algorithm
Last Updated :
01 Aug, 2023
In real-world machine learning applications, it is common to have many relevant features, but only a subset of them may be observable. When dealing with variables that are sometimes observable and sometimes not, it is indeed possible to utilize the instances when that variable is visible or observed in order to learn and make predictions for the instances where it is not observable. This approach is often referred to as handling missing data. By using the available instances where the variable is observable, machine learning algorithms can learn patterns and relationships from the observed data. These learned patterns can then be used to predict the values of the variable in instances where it is missing or not observable.
The expectation-Maximization algorithm can be used to handle situations where variables are partially observable. When certain variables are observable, we can use those instances to learn and estimate their values. Then, we can predict the values of these variables in instances when it is not observable.
The EM algorithm was proposed and named in a seminal paper published in 1977 by Arthur Dempster, Nan Laird, and Donald Rubin. Their work formalized the algorithm and demonstrated its usefulness in statistical modeling and estimation.
EM algorithm is applicable to latent variables, which are variables that are not directly observable but are inferred from the values of other observed variables. By leveraging the known general form of the probability distribution governing these latent variables, the EM algorithm can predict their values.
The EM algorithm serves as the foundation for many unsupervised clustering algorithms in the field of machine learning. It provides a framework to find the local maximum likelihood parameters of a statistical model and infer latent variables in cases where data is missing or incomplete.
Expectation-Maximization (EM) Algorithm
The Expectation-Maximization (EM) algorithm is an iterative optimization method that combines different unsupervised machine learning algorithms to find maximum likelihood or maximum posterior estimates of parameters in statistical models that involve unobserved latent variables. The EM algorithm is commonly used for latent variable models and can handle missing data. It consists of an estimation step (E-step) and a maximization step (M-step), forming an iterative process to improve model fit.
- In the E step, the algorithm computes the latent variables i.e. expectation of the log-likelihood using the current parameter estimates.
- In the M step, the algorithm determines the parameters that maximize the expected log-likelihood obtained in the E step, and corresponding model parameters are updated based on the estimated latent variables.

Expectation-Maximization in EM Algorithm
By iteratively repeating these steps, the EM algorithm seeks to maximize the likelihood of the observed data. It is commonly used for unsupervised learning tasks, such as clustering, where latent variables are inferred and has applications in various fields, including machine learning, computer vision, and natural language processing.
Key Terms in Expectation-Maximization (EM) Algorithm
Some of the most commonly used key terms in the Expectation-Maximization (EM) Algorithm are as follows:
- Latent Variables: Latent variables are unobserved variables in statistical models that can only be inferred indirectly through their effects on observable variables. They cannot be directly measured but can be detected by their impact on the observable variables.
- Likelihood: It is the probability of observing the given data given the parameters of the model. In the EM algorithm, the goal is to find the parameters that maximize the likelihood.
- Log-Likelihood: It is the logarithm of the likelihood function, which measures the goodness of fit between the observed data and the model. EM algorithm seeks to maximize the log-likelihood.
- Maximum Likelihood Estimation (MLE): MLE is a method to estimate the parameters of a statistical model by finding the parameter values that maximize the likelihood function, which measures how well the model explains the observed data.
- Posterior Probability: In the context of Bayesian inference, the EM algorithm can be extended to estimate the maximum a posteriori (MAP) estimates, where the posterior probability of the parameters is calculated based on the prior distribution and the likelihood function.
- Expectation (E) Step: The E-step of the EM algorithm computes the expected value or posterior probability of the latent variables given the observed data and current parameter estimates. It involves calculating the probabilities of each latent variable for each data point.
- Maximization (M) Step: The M-step of the EM algorithm updates the parameter estimates by maximizing the expected log-likelihood obtained from the E-step. It involves finding the parameter values that optimize the likelihood function, typically through numerical optimization methods.
- Convergence: Convergence refers to the condition when the EM algorithm has reached a stable solution. It is typically determined by checking if the change in the log-likelihood or the parameter estimates falls below a predefined threshold.
How Expectation-Maximization (EM) Algorithm Works:
The essence of the Expectation-Maximization algorithm is to use the available observed data of the dataset to estimate the missing data and then use that data to update the values of the parameters. Let us understand the EM algorithm in detail.
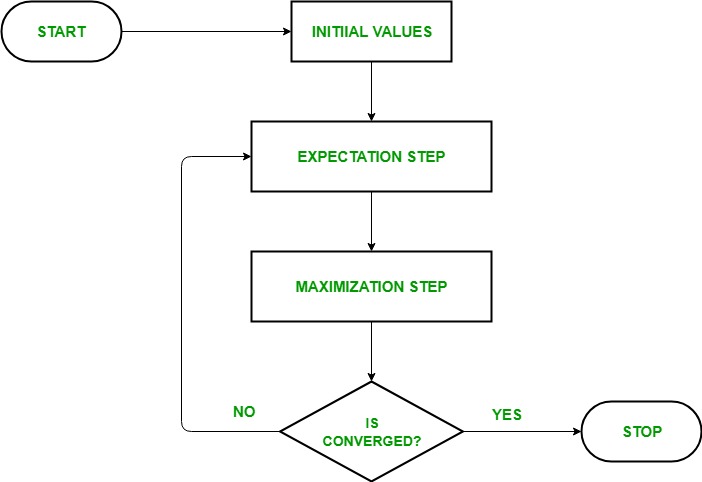
EM Algorithm Flowchart
- Initialization:
- Initially, a set of initial values of the parameters are considered. A set of incomplete observed data is given to the system with the assumption that the observed data comes from a specific model.
- E-Step (Expectation Step): In this step, we use the observed data in order to estimate or guess the values of the missing or incomplete data. It is basically used to update the variables.
- Compute the posterior probability or responsibility of each latent variable given the observed data and current parameter estimates.
- Estimate the missing or incomplete data values using the current parameter estimates.
- Compute the log-likelihood of the observed data based on the current parameter estimates and estimated missing data.
- M-step (Maximization Step): In this step, we use the complete data generated in the preceding “Expectation” – step in order to update the values of the parameters. It is basically used to update the hypothesis.
- Update the parameters of the model by maximizing the expected complete data log-likelihood obtained from the E-step.
- This typically involves solving optimization problems to find the parameter values that maximize the log-likelihood.
- The specific optimization technique used depends on the nature of the problem and the model being used.
- Convergence: In this step, it is checked whether the values are converging or not, if yes, then stop otherwise repeat step-2 and step-3 i.e. “Expectation” – step and “Maximization” – step until the convergence occurs.
- Check for convergence by comparing the change in log-likelihood or the parameter values between iterations.
- If the change is below a predefined threshold, stop and consider the algorithm converged.
- Otherwise, go back to the E-step and repeat the process until convergence is achieved.
Expectation-Maximization Algorithm Step by Step Implementation
Import the necessary libraries
Python3
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
|
Generate a dataset with two Gaussian components
Python3
mu1, sigma1 = 2, 1
mu2, sigma2 = -1, 0.8
X1 = np.random.normal(mu1, sigma1, size=200)
X2 = np.random.normal(mu2, sigma2, size=600)
X = np.concatenate([X1, X2])
sns.kdeplot(X)
plt.xlabel('X')
plt.ylabel('Density')
plt.title('Density Estimation of X')
plt.show()
|
Output:

Density Plot
Initialize parameters
Python3
mu1_hat, sigma1_hat = np.mean(X1), np.std(X1)
mu2_hat, sigma2_hat = np.mean(X2), np.std(X2)
pi1_hat, pi2_hat = len(X1) / len(X), len(X2) / len(X)
|
Perform EM algorithm
- Iterates for the specified number of epochs (20 in this case).
- In each epoch, the E-step calculates the responsibilities (gamma values) by evaluating the Gaussian probability densities for each component and weighting them by the corresponding proportions.
- The M-step updates the parameters by computing the weighted mean and standard deviation for each component
Python3
num_epochs = 20
log_likelihoods = []
for epoch in range(num_epochs):
gamma1 = pi1_hat * norm.pdf(X, mu1_hat, sigma1_hat)
gamma2 = pi2_hat * norm.pdf(X, mu2_hat, sigma2_hat)
total = gamma1 + gamma2
gamma1 /= total
gamma2 /= total
mu1_hat = np.sum(gamma1 * X) / np.sum(gamma1)
mu2_hat = np.sum(gamma2 * X) / np.sum(gamma2)
sigma1_hat = np.sqrt(np.sum(gamma1 * (X - mu1_hat)**2) / np.sum(gamma1))
sigma2_hat = np.sqrt(np.sum(gamma2 * (X - mu2_hat)**2) / np.sum(gamma2))
pi1_hat = np.mean(gamma1)
pi2_hat = np.mean(gamma2)
log_likelihood = np.sum(np.log(pi1_hat * norm.pdf(X, mu1_hat, sigma1_hat)
+ pi2_hat * norm.pdf(X, mu2_hat, sigma2_hat)))
log_likelihoods.append(log_likelihood)
plt.plot(range(1, num_epochs+1), log_likelihoods)
plt.xlabel('Epoch')
plt.ylabel('Log-Likelihood')
plt.title('Log-Likelihood vs. Epoch')
plt.show()
|
Output:

Epoch vs Log-likelihood
Plot the final estimated density
Python3
X_sorted = np.sort(X)
density_estimation = pi1_hat*norm.pdf(X_sorted,
mu1_hat,
sigma1_hat) + pi2_hat * norm.pdf(X_sorted,
mu2_hat,
sigma2_hat)
plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color='green', linewidth=2)
plt.plot(X_sorted, density_estimation, color='red', linewidth=2)
plt.xlabel('X')
plt.ylabel('Density')
plt.title('Density Estimation of X')
plt.legend(['Kernel Density Estimation','Mixture Density'])
plt.show()
|
Output:

Estimated density
Applications of the EM algorithm
- It can be used to fill in the missing data in a sample.
- It can be used as the basis of unsupervised learning of clusters.
- It can be used for the purpose of estimating the parameters of the Hidden Markov Model (HMM).
- It can be used for discovering the values of latent variables.
Advantages of EM algorithm
- It is always guaranteed that likelihood will increase with each iteration.
- The E-step and M-step are often pretty easy for many problems in terms of implementation.
- Solutions to the M-steps often exist in the closed form.
Disadvantages of EM algorithm
- It has slow convergence.
- It makes convergence to the local optima only.
- It requires both the probabilities, forward and backward (numerical optimization requires only forward probability).
Share your thoughts in the comments
Please Login to comment...