Silhouette Algorithm to determine the optimal value of k

One of the fundamental steps of an unsupervised learning algorithm is to determine the number of clusters into which the data may be divided. The silhouette algorithm is one of the many algorithms to determine the optimal number of clusters for an unsupervised learning technique. In the Silhouette algorithm, we assume that the data has already been clustered into k clusters by a clustering technique(Typically K-Means Clustering technique). 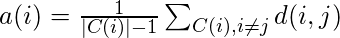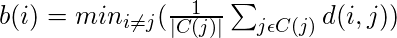Then for each data point, we define the following:- C(i) -The cluster assigned to the ith data point |C(i)| – The number of data points in the cluster assigned to the ith data point a(i) – It gives a measure of how well assigned the ith data point is to it’s cluster b(i) – It is defined as the average dissimilarity to the closest cluster which is not it’s cluster The silhouette coefficient s(i) is given by:- 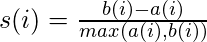We determine the average silhouette for each value of k and for the value of k which has the maximum value of s(i) is considered the optimal number of clusters for the unsupervised learning algorithm. Let us consider the following data:-

S.No	X1	X2
1.	-7.36	6.37
2.	3.08	-6.78
3.	5.03	-8.31
4.	-1.93	-0.92
5.	-8.86	6.60

We now iterate the values of k from 2 to 5. We assume that no practical data exists for which all the data points can be optimally clustered into 1 cluster. We construct the following tables for each value of k:- k = 2

S.No	a(i)	b(i)	s(i)
1.	5.31	14.1	0.62
2.	2.47	13.15	0.81
3.	2.47	14.97	0.84
4.	9.66	8.93	-0.076
5.	5.88	19.16	0.69

Average value of s(i) = 0.58 k = 3

S.No	a(i)	b(i)	s(i)
1.	1.52	9.09	0.83
2.	2.47	7.71	0.68
3.	2.47	10.15	0.76
4.	0	7.71	1
5.	1.52	17.93	0.92

Average value of s(i) = 0.84 k = 4

S.No	a(i)	b(i)	s(i)
1.	1.52	9.09	0.83
2.	infinite	2.47	0
3.	infinite	2.47	0
4.	infinite	7.71	0
5.	1.52	10.23	0.85

Average value of s(i) = 0.37 k = 5

S.No	a(i)	b(i)	s(i)
1.	infinite	1.52	0
2.	infinite	2.47	0
3.	infinite	2.47	0
4.	infinite	7.71	0
5.	infinite	1.52	0

Average value of s(i) = 0 We see that the highest value of s(i) exists for k = 3. Therefore we conclude that the optimal number of clusters for the given data is 3.