Mathematics | Sequence, Series and Summations
Last Updated :
25 Nov, 2022
SEQUENCE:
It is a set of numbers in a definite order according to some definite rule (or rules).
Each number of the set is called a term of the sequence and its length is the number of terms in it. We can write the sequence as
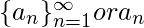
. A finite sequence is generally described by a
1, a
2, a
3…. a
n, and an infinite sequence is described by a
1, a
2, a
3…. to infinity. A sequence {a
n} has the limit L and we write
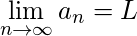
or
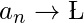
as
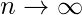
.
For example:
2, 4, 6, 8 ...., 20 is a finite sequence obtained by adding 2 to the previous number.
10, 6, 2, -2, ..... is an infinite sequence obtained by subtracting 4 from the previous number.
If the terms of a sequence can be described by a formula, then the sequence is called a
progression.
1, 1, 2, 3, 5, 8, 13, ....., is a progression called the Fibonacci sequence in which each term
is the sum of the previous two numbers.
More about progressions
Theorems:
Theorem 1: Given the sequence 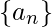 if we have a function f(x) such that f(n) =
if we have a function f(x) such that f(n) = 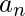 and
and 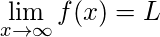 then
then 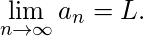
This theorem is basically telling us that we take the limits of sequences much like we take the limit of functions.
Theorem 2 (Squeeze Theorem): If 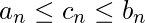 for all n > N for some N and
for all n > N for some N and 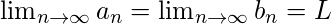 then
then 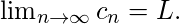 Theorem 3: If
Theorem 3: If 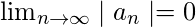 then
then 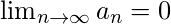 .
. Note that in order for this theorem to hold the limit MUST be zero and it won’t work for a sequence whose limit is not zero.
Theorem 4: If  and the function f is continuous at L, then
and the function f is continuous at L, then 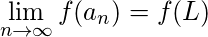 Theorem 5: The sequence
Theorem 5: The sequence 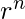 is convergent if
is convergent if 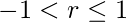 and divergent for
all other values of r. Also,
and divergent for
all other values of r. Also,

This theorem is a useful theorem giving the convergence/divergence and value (for when it’s convergent) of a sequence that arises on occasion.
Properties:
If
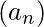
and
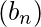
are convergent sequences, the following properties hold:
-
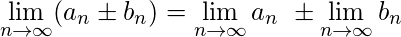
-
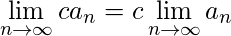
-
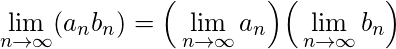
-
![Rendered by QuickLaTeX.com \displaystyle\lim_{n\to\infty} {a_n}^p = \Big[\displaystyle\lim_{n\to\infty} a_n\Big]^p](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a1c1b3c9f7ec2a1cbd26ceb17ca3a7ec_l3.png) provided
provided 
And the last property is

SERIES:
A series is simply the sum of the various terms of a sequence.
If the sequence is 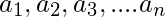 the expression
the expression 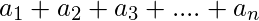 is called the series associated with it. A series is represented by ‘S’ or the Greek symbol
is called the series associated with it. A series is represented by ‘S’ or the Greek symbol 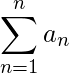 . The series can be finite or infinite.
Examples:
. The series can be finite or infinite.
Examples:
5 + 2 + (-1) + (-4) is a finite series obtained by subtracting 3 from the previous number.
1 + 1 + 2 + 3 + 5 is an infinite series called the Fibonacci series obtained from the
Fibonacci sequence.
If the sequence of partial sums is a convergent sequence (i.e. its limit exists and is finite) then the series is also called
convergent i.e. if
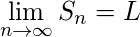
then
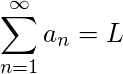
. Likewise, if the sequence of partial sums is a divergent sequence (i.e. if
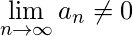
or its limit doesn’t exist or is plus or minus infinity) then the series is also called divergent.
Properties:
If 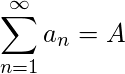 and
and 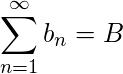 be convergent series then
be convergent series then 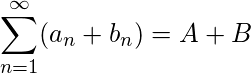 If
If 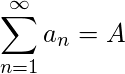 and
and 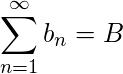 be convergent series then
be convergent series then 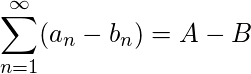 If
If 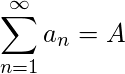 be convergent series then
be convergent series then 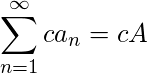 If
If 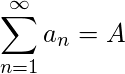 and
and 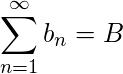 be convergent series then if
be convergent series then if 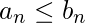 for all n
for all n 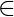 N then
N then 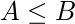
Theorems:
Theorem 1 (Comparison test): Suppose 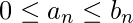 for
for 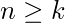 for some k. Then
(1) The convergence of
for some k. Then
(1) The convergence of 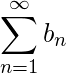 implies the convergence of
implies the convergence of 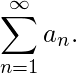 (2) The convergence of
(2) The convergence of 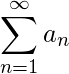 implies the convergence of
implies the convergence of 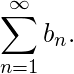 Theorem 2 (Limit Comparison test): Let
Theorem 2 (Limit Comparison test): Let  and
and  , and suppose that
, and suppose that 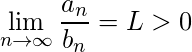 . Then
. Then 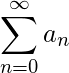 converges if and only if
converges if and only if 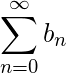 converges.
Theorem 3 (Ratio test): Suppose that the following limit exists,
converges.
Theorem 3 (Ratio test): Suppose that the following limit exists, 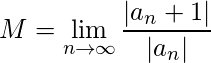 . Then,
(1) If
. Then,
(1) If 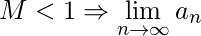 converges
(2) If
converges
(2) If 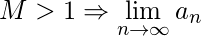 diverges
(3) If
diverges
(3) If 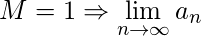 might either converge or diverge
Theorem 4 (Root test): Suppose that the following limit exists:,
might either converge or diverge
Theorem 4 (Root test): Suppose that the following limit exists:, ![Rendered by QuickLaTeX.com M = \displaystyle\lim_{n\to\infty}\sqrt[n]{|a_n|}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7ceb37eaac2861f1236afb4011125909_l3.png) . Then,
(1) If
. Then,
(1) If 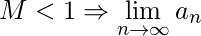 converges
(2) If
converges
(2) If 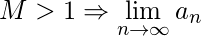 diverges
(3) If
diverges
(3) If 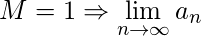 might either converge or diverge
Theorem 5 (Absolute Convergence test): A series
might either converge or diverge
Theorem 5 (Absolute Convergence test): A series 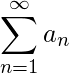 is said to be absolutely convergent if the series
is said to be absolutely convergent if the series 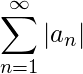 converges.
Theorem 6 (Conditional Convergence test): A series
converges.
Theorem 6 (Conditional Convergence test): A series 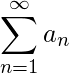 is said to be conditionally convergent if the series
is said to be conditionally convergent if the series 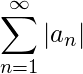 diverges but the series
diverges but the series 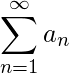 converges .
Theorem 7 (Alternating Series test): If
converges .
Theorem 7 (Alternating Series test): If 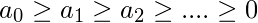 , and
, and 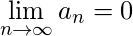 , the ‘alternating series’
, the ‘alternating series’ 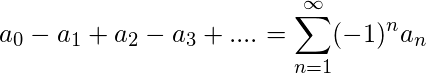 will converge.
Series Questions
will converge.
Series Questions
SUMMATIONS:
Summation is the addition of a sequence of numbers. It is a convenient and simple form of shorthand used to give a concise expression for a sum of the values of a variable.
The summation symbol,
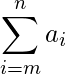
, instructs us to sum the elements of a sequence. A typical element of the sequence which is being summed appears to the right of the summation sign.
Properties:
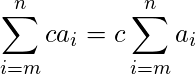 where c is any number. So, we can factor constants out of a summation.
where c is any number. So, we can factor constants out of a summation.
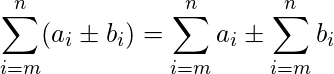 So we can break up a summation across a sum or difference.
So we can break up a summation across a sum or difference.
Note that while we can break up sums and differences as mentioned above, we can’t do the same thing for products and quotients. In other words,

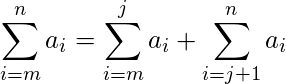 , for any natural number
, for any natural number 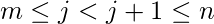 .
.
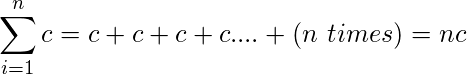 . If the argument of the summation is a constant, then the sum is the limit range value times the constant.
. If the argument of the summation is a constant, then the sum is the limit range value times the constant.
Examples:
1) Sum of first n natural numbers: 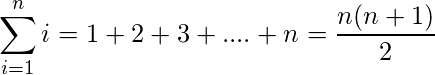 .
2) Sum of squares of first n natural numbers:
.
2) Sum of squares of first n natural numbers:
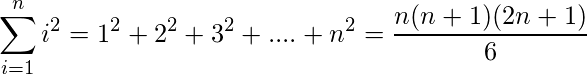 .
3) Sum of cubes of first n natural numbers:
.
3) Sum of cubes of first n natural numbers:
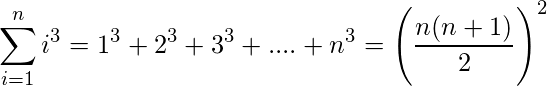 .
4) The property of logarithms:
.
4) The property of logarithms:
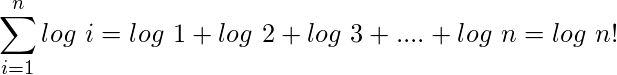 .
.
Share your thoughts in the comments
Please Login to comment...