Different Operations on Matrices

For an introduction to matrices, you can refer to the following article: Matrix Introduction
In this article, we will discuss the following operations on matrices and their properties: 

• Matrices Addition
• Matrices Subtraction
• Matrices Multiplication

Matrices Addition:

The addition of two matrices A _m*n and B_m*n gives a matrix C_m*n. The elements of C are the sum of corresponding elements in A and B which can be shown as: 

Key points:

• The addition of matrices is commutative, which means A+B = B+A
• The addition of matrices is associative, which means A+(B+C) = (A+B)+C
• The order of matrices A, B, and A+B is always the same
• If the order of A and B are different, A+B can’t be computed
• The complexity of the addition operation is O(M*N) where M*N is the order of matrices

Implementation of the above approach:

C++

// C++ Program for matrix addition

#include <iostream>
using namespace std;

int main()
{

    int n = 2, m = 2;
    int a[n][m] = { { 2, 5 }, { 1, 7 } };
    int b[n][m] = { { 3, 7 }, { 2, 9 } };

    int c[n][m];
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++) {
            c[i][j] = a[i][j] + b[i][j];
        }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++)
            cout << c[i][j] << " ";
        cout << endl;
    }
}

Java

// Java program for addition
// of two matrices
import java.util.*;
class GFG
{

  // Driver code
  public static void main(String[] args)
  {
    int n = 2, m = 2;
    int a[][] = { { 2, 5 }, { 1, 7 } };

    int b[][] = { { 3, 7 }, { 2, 9 } };

    // To store result
    int c[][] = new int[n][m];

    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++)
        c[i][j] = a[i][j] + b[i][j];
    }

    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++)
        System.out.print(c[i][j] + " ");
      System.out.print("\n");
    }
  }
}

// This code is contributed by Aarti_Rathi

Python3

# Python3 program for addition
# of two matrices

N = 4
# This function adds A[][]
# and B[][], and stores
# the result in C[][]


# driver code
a = [ [2, 5],
    [1, 7]]

b= [ [3, 7],
    [2, 9]]

N = 2

c=a[:][:] # To store result

for i in range(N):
    for j in range(N):
        c[i][j] = a[i][j] + b[i][j]


for i in range(N):
    for j in range(N):
        print(c[i][j], " ", end='')
    print()

# This code is contributed by Aarti_Rathi

C#

// C# program to rotate a
// matrix by 90 degrees
using System;
class GFG {

  // Driver Code
  static public void Main()
  {
    int N = 2;
    int M = 2;

    // Test Case 1
    int[,] a = { { 2, 5 }, { 1, 7 } };
    int[,] b = { { 3, 7 }, { 2, 9 } };

    int [,] c =new int[N,M];
    for (int i = 0; i < N; i++)
      for (int j = 0; j < M; j++) {
        c[i,j] = a[i,j] + b[i,j];
      }

    for (int i = 0; i < N; i++) {
      for (int j = 0; j < M; j++)
        Console.Write(c[i,j] + " ");
      Console.WriteLine();
    }
  }
}

// This code is contributed by Aarti_Rathi

Javascript

<script>

// Javascript Program for matrix addition
var n = 2, m = 2;
var a = [[ 2, 5 ], [ 1, 7 ]];
var b = [[ 3, 7 ], [ 2, 9 ]];
var c = Array.from(Array(n), ()=>Array(m).fill(0));
for (var i = 0; i < n; i++)
    for (var j = 0; j < n; j++) {
        c[i][j] = a[i][j] + b[i][j];
    }
for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++)
        document.write( c[i][j] + " ");
    document.write("<br>");
}

// This code is contributed by noob2000.
</script>

Output

5 12 
3 16 

Complexity analysis:

• Time Complexity: O(N*M)
• Auxiliary Space: O(N*M)

Matrices Subtraction:

The subtraction of two matrices A_m*n and B_m*n give a matrix C_m*n. The elements of C are difference of corresponding elements in A and B which can be represented as: 

Key points:

• Subtraction of matrices is non-commutative which means A-B ≠ B-A
• Subtraction of matrices is non-associative which means A-(B-C) ≠ (A-B)-C
• The order of matrices A, B, and A – B is always the same
• If the order of A and B are different, A – B can’t be computed
• The complexity of subtraction operation is O(M*N) where M*N is the order of matrices

Implementation of the above approach:

C++

// C++ Program for matrix subtraction

#include <iostream>
using namespace std;

int main()
{

    int n = 2, m = 2;
    int a[n][m] = { { 2, 5 }, { 1, 7 } };
    int b[n][m] = { { 3, 7 }, { 2, 9 } };

    int c[n][m];
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++) {
            c[i][j] = a[i][j] - b[i][j];
        }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++)
            cout << c[i][j] << " ";
        cout << endl;
    }
}

Java

public class GFG {
    // Java Program for matrix subtraction

    public static void main(String[] args)
    {

        int n = 2;
        int m = 2;
        int[][] a = { { 2, 5 }, { 1, 7 } };
        int[][] b = { { 3, 7 }, { 2, 9 } };

        int[][] c = new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                c[i][j] = a[i][j] - b[i][j];
            }
        }

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                System.out.print(c[i][j]);
                System.out.print(" ");
            }
            System.out.print("\n");
        }
    }
}

// This code is contributed by Aarti_Rathi

Python3

# Python3 program for addition
# of two matrices
N = 4

# This function adds A[][]
# and B[][], and stores
# the result in C[][]

# driver code
a = [[2, 5],
     [1, 7]]

b = [[3, 7],
     [2, 9]]

N = 2

c = a[:][:]  # To store result

for i in range(N):
    for j in range(N):
        c[i][j] = a[i][j] - b[i][j]


for i in range(N):
    for j in range(N):
        print(c[i][j], " ", end='')
    print()

# This code is contributed by Aarti_Rathi

C#

// C# program to rotate a
// matrix by 90 degrees
using System;

class GFG {

     // Driver Code
    static public void Main()
    {
        int N = 2;
        int M = 2;

        // Test Case 1
        int[,] a = { { 2, 5 }, { 1, 7 } };
        int[,] b = { { 3, 7 }, { 2, 9 } };

        int [,] c =new int[N,M];
        for (int i = 0; i < N; i++)
            for (int j = 0; j < M; j++) {
                c[i,j] = a[i,j] - b[i,j];
            }

        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++)
                Console.Write(c[i,j] + " ");
            Console.WriteLine();
        }
    }
}

// This code is contributed by Aarti_Rathi

Javascript

<script>

// Javascript Program for matrix subtraction
var n = 2, m = 2;
var a = [[ 2, 5 ], [ 1, 7 ]];
var b = [[ 3, 7 ], [ 2, 9 ]];
var c = Array.from(Array(n), ()=>Array(m).fill(0));
for (var i = 0; i < n; i++)
    for (var j = 0; j < n; j++) {
        c[i][j] = a[i][j] - b[i][j];
    }
for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++)
        document.write( c[i][j] + " ");
    document.write("<br>");
}

// This code is contributed by akshitsaxena09
</script>

Output

-1 -2 
-1 -2 

Complexity Analysis:

• Time Complexity: O(N*M)
• Auxiliary Space: O(N*M)

Matrices Multiplication:

The multiplication of two matrices A_m*n and B_n*p give a matrix C_m*p. It means a number of columns in A must be equal to the number of rows in B to calculate C=A*B. To calculate element c11, multiply elements of 1st row of A with 1st column of B and add them (5*1+6*4) which can be shown as:

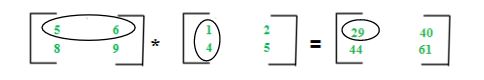
Key points:

• Multiplication of matrices is non-commutative which means A*B ≠ B*A
• Multiplication of matrices is associative which means A*(B*C) = (A*B)*C
• For computing A*B, the number of columns in A must be equal to the number of rows in B
• The existence of A*B does not imply the existence of B*A
• The complexity of multiplication operation (A*B) is O(m*n*p) where m*n and n*p are the order of A and B respectively
• The order of matrix C computed as A*B is m*p where m*n and n*p are the order of A and B respectively

Implementation of the above approach:

C++

// C++ Program for matrix Multiplication

#include <iostream>
using namespace std;

int main()
{

    int n = 2, m = 2;
    int a[n][m] = { { 2, 5 }, { 1, 7 } };
    int b[n][m] = { { 3, 7 }, { 2, 9 } };

    int c[n][m];
    int i, j, k;
    for (i = 0; i < n; i++)
    {
        for (j = 0; j < n; j++)
        {
            c[i][j] = 0;
            for (k = 0; k < n; k++)
                c[i][j] += a[i][k] * b[k][j];
        }
    }

    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
            cout << c[i][j] << " ";
        cout << endl;
    }
}

Java

// Java program for matrix multiplication
import java.io.*;

class GFG {
  public static void main(String[] args)
  {
    int n = 2, m = 2;

    int a[][] = { { 2, 5 }, { 1, 7 } };
    int b[][] = { { 3, 7 }, { 2, 9 } };

    int c[][] = new int[n][m];
    int i, j, k;
    for (i = 0; i < n; i++) {
      for (j = 0; j < n; j++) {
        c[i][j] = 0;
        for (k = 0; k < n; k++) {
          c[i][j] += a[i][k] * b[k][j];
        }
      }
    }
    for (i = 0; i < n; i++) {
      for (j = 0; j < n; j++) {
        System.out.print(c[i][j] + " ");
      }
      System.out.println();
    }
  }
}

// This code is contributed by ishankhandelwals.

Python

# Python code for matrix multiplication
a = [[2, 5], [1, 7]]
b = [[3, 7], [2, 9]]
c = [[0, 0], [0, 0]]
for i in range(0, 2):
    for j in range(0, 2):
        c[i][j] = 0
        for k in range(0, 2):
            c[i][j] = c[i][j]+(a[i][k]*b[k][j])
for i in range(0, 2):
    for j in range(0, 2):
        print(c[i][j])

        # This code is contributed by ishankhandelwals.

C#

// C# program to rotate a
// matrix by 90 degrees
using System;

class GFG {

  // Driver Code
  static public void Main()
  {
    int N = 2;
    int M = 2;

    // Test Case 1
    int[,] a = { { 2, 5 }, { 1, 7 } };
    int[,] b = { { 3, 7 }, { 2, 9 } };

    int [,] c =new int[N,M];

    for (int i = 0; i < N; i++)
    {
      for (int j = 0; j < M; j++) {
        c[i,j]=0;
        for(int k=0;k<N;k++)
          c[i,j] = c[i,j]+(a[i,k] * b[k,j]);
      }
    }

    for (int i = 0; i < N; i++) {
      for (int j = 0; j < M; j++)
        Console.Write(c[i,j] + " ");
      Console.WriteLine();
    }
  }
}

// This code is contributed by Aarti_Rathi

Javascript

<script>

// Javascript Program for matrix multiplication
var n = 2, m = 2;
var a = [[ 2, 5 ], [ 1, 7 ]];
var b = [[ 3, 7 ], [ 2, 9 ]];
var c = Array.from(Array(n), ()=>Array(m).fill(0));
for (var i = 0; i < n; i++){
    for (var j = 0; j < n; j++) {
        c[i][j] = 0;
        for (var k = 0; k < n; k++) {
            c[i][j] += a[i][k] * b[k][j];
    }
    }}
for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++)
        document.write( c[i][j] + " ");
    document.write("<br>");
}

// This code is contributed by Sajal Aggarwal.
</script>

Output

16 59 
17 70 

Complexity Analysis:

• Time Complexity: O((N²)*M)
• Auxiliary Space: O(N*M)