Relationship between number of nodes and height of binary tree
Last Updated :
05 Feb, 2024
Prerequisite – Binary Tree Data Structure
In this article, we will discuss various cases for relationship between number of nodes and height of binary tree. Before understanding this article, you should have basic idea about binary trees and their properties.
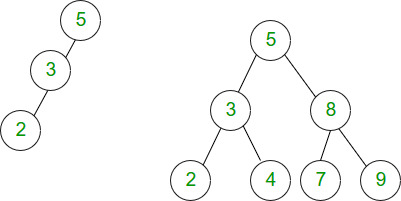
The height of the binary tree is the longest path from root node to any leaf node in the tree. For example, the height of binary tree shown in Figure 1(b) is 2 as longest path from root node to node 2 is 2. Also, the height of binary tree shown in Figure 1(a) is 4.
Binary Tree :
In a binary tree, a node can have a maximum of two children.
Calculating minimum and maximum height from a number of nodes –
If there are n nodes in a binary tree, the maximum height of the binary tree is n-1, and the minimum height is floor (log2(n)+1).
For example, the left skewed binary tree shown in Figure 1(a) with 5 nodes has a height of 5-1 = 4, and the binary tree shown in Figure 1(b) with 5 nodes has a height floor(log25) = 2.

Calculating minimum and maximum number of nodes from height:
If binary tree has height h, minimum number of nodes is h+1 (in case of left skewed and right skewed binary tree).
For example, the binary tree shown in Figure 2(a) with height 2 has 3 nodes.
If binary tree has height h, maximum number of nodes will be when all levels are completely full. Total number of nodes will be 2^0 + 2^1 + …. 2^h = 2^(h+1)-1.
For example, the binary tree shown in Figure 2(b) with height 2 has 2^(2+1)-1 = 7 nodes.
Binary Search Tree:
In a binary search tree, left child of a node has value less than the parent and right child has value greater than parent.
Calculating minimum and maximum height from the number of nodes:
If there are n nodes in a binary search tree, maximum height of the binary search tree is n-1 and minimum height is ceil(log2(n)+1).
Calculating minimum and maximum number of nodes from height:
If binary search tree has height h, minimum number of nodes is h+1 (in case of left skewed and right skewed binary search tree).
If binary search tree has height h, maximum number of nodes will be when all levels are completely full. Total number of nodes will be 2^0 + 2^1 + …. 2^h = 2^(h+1)-1.
All the rules in BST are same as in binary tree and can be visualized in the same way.
Que-1. The height of a tree is the length of the longest root-to-leaf path in it. The maximum and the minimum number of nodes in a binary tree of height 5 are:
- (A) 63 and 6, respectively
- (B) 64 and 5, respectively
- (C) 32 and 6, respectively
- (D) 31 and 5, respectively
Solution: According to formula discussed,
max number of nodes = 2^(h+1)-1 = 2^6-1 =63.
min number of nodes = h+1 = 5+1 = 6.
Que-2. Which of the following height is not possible for a binary tree with 50 nodes?
- (A) 4
- (B) 5
- (C) 6
- (D) None
Solution: According to formula discussed,
Minimum height with 50 nodes = floor(log250) = 5. Therefore, height 4 is not possible.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...