Prerequisite – Graph Theory Basics – Set 1
1. Walk –
A walk is a sequence of vertices and edges of a graph i.e. if we traverse a graph then we get a walk.
Edge and Vertices both can be repeated.
Here, 1->2->3->4->2->1->3 is a walk.
Walk can be open or closed.
Open walk- A walk is said to be an open walk if the starting and ending vertices are different i.e. the origin vertex and terminal vertex are different.
Closed walk- A walk is said to be a closed walk if the starting and ending vertices are identical i.e. if a walk starts and ends at the same vertex, then it is said to be a closed walk.
In the above diagram:
1->2->3->4->5->3 is an open walk.
1->2->3->4->5->3->1 is a closed walk.
2. Trail –
Trail is an open walk in which no edge is repeated.
Vertex can be repeated.
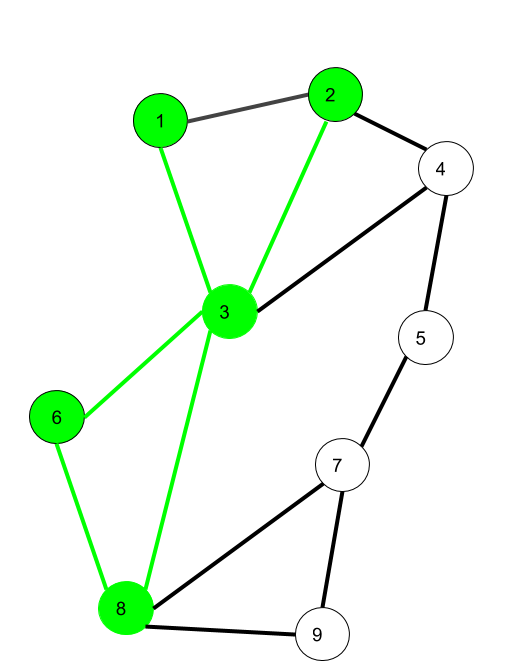
Here 1->3->8->6->3->2 is trail
Also 1->3->8->6->3->2->1 will be a closed trail
3. Circuit –
Traversing a graph such that not an edge is repeated but vertex can be repeated and it is closed also i.e. it is a closed trail.
Vertex can be repeated.
Edge can not be repeated.
Here 1->2->4->3->6->8->3->1 is a circuit.
Circuit is a closed trail.
These can have repeated vertices only.
4. Path –
It is a trail in which neither vertices nor edges are repeated i.e. if we traverse a graph such that we do not repeat a vertex and nor we repeat an edge. As path is also a trail, thus it is also an open walk.
Another definition for path is a walk with no repeated vertex. This directly implies that no edges will ever be repeated and hence is redundant to write in the definition of path.
Vertex not repeated
Edge not repeated
Here 6->8->3->1->2->4 is a Path
5. Cycle –
Traversing a graph such that we do not repeat a vertex nor we repeat a edge but the starting and ending vertex must be same i.e. we can repeat starting and ending vertex only then we get a cycle.
Vertex not repeated
Edge not repeated
Here 1->2->4->3->1 is a cycle.
Cycle is a closed path.
These can not have repeat anything (neither edges nor vertices).
Note that for closed sequences start and end vertices are the only ones that can repeat.