Mathematics | Graph theory practice questions
Last Updated :
18 Sep, 2023
Problem 1 – There are 25 telephones in Geeksland. Is it possible to connect them with wires so that each telephone is connected with exactly 7 others.
Solution – Let us suppose that such an arrangement is possible. This can be viewed as a graph in which telephones are represented using vertices and wires using the edges. Now we have 25 vertices in this graph. The degree of each vertex in the graph is 7. From handshaking lemma, we know.
sum of degrees of all vertices = 2*(number of edges)
number of edges = (sum of degrees of all vertices) / 2
We need to understand that an edge connects two vertices. So the sum of degrees of all the vertices is equal to twice the number of edges. Therefore,
25*7 = 2*(number of edges)
number of edges = 25*7 / 2 = 87.5
This is not an integer. As a result we can conclude that our supposition is wrong and such an arrangement is not possible.
Problem 2 – The figure below shows an arrangement of knights on a 3*3 grid.

Figure – initial state Is it possible to reach the final state as shown below using valid knight’s moves ?

Figure – final state Solution – NO. You might think you need to be a good chess player in order to crack the above question. However the above question can be solved using graphs. But what kind of a graph should we draw? Let each of the 9 vertices be represented by a number as shown below.
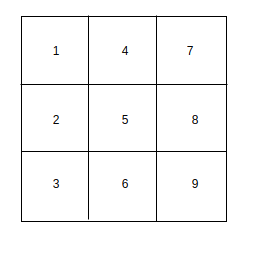
Now we consider each square of the grid as a vertex in our graph. There exists a edge between two vertices in our graph if a valid knight’s move is possible between the corresponding squares in the graph. For example – If we consider square 1. The reachable squares with valid knight’s moves are 6 and 8. We can say that vertex 1 is connected to vertices 6 and 8 in our graph. Similarly we can draw the entire graph as shown below. Clearly vertex 5 can’t be reached from any of the squares. Hence none of the edges connect to vertex 5.
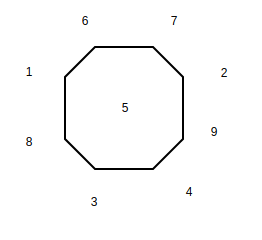
We use a hollow circle to depict a white knight in our graph and a filled circle to depict a black knight. Hence the initial state of the graph can be represented as :
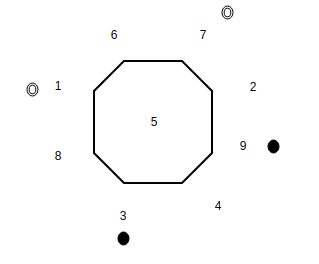
Figure – initial state The final state is represented as :
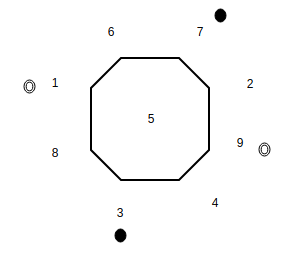
Figure – final state Note that in order to achieve the final state there needs to exist a path where two knights (a black knight and a white knight cross-over). We can only move the knights in a clockwise or counter-clockwise manner on the graph (If two vertices are connected on the graph: it means that a corresponding knight’s move exists on the grid). However the order in which knights appear on the graph cannot be changed. There is no possible way for a knight to cross over (Two knights cannot exist on one vertex) the other in order to achieve the final state. Hence, we can conclude that no matter what the final arrangement is not possible.
Problem 3: There are 9 line segments drawn in a plane. Is it possible that each line segment intersects exactly 3 others?
Solution: This problem seems very difficult initially. We could think of solving it using graphs. But how do we do draw the graph. If we try to approach this problem by using line segments as edges of a graph,we seem to reach nowhere (This sounds confusing initially). Here we need to consider a graph where each line segment is represented as a vertex. Now two vertices of this graph are connected if the corresponding line segments intersect. Now this graph has 9 vertices. The degree of each vertex is 3.
We know that for a graph
Sum of degrees of all vertices = 2* Number of Edges in the graph
Since the sum of degrees of vertices in the above problem is 9*3 = 27 i.e odd, such an arrangement is not possible.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...