Mathematics | Rings, Integral domains and Fields

Prerequisite – Mathematics | Algebraic Structure

Ring – Let addition (+) and Multiplication (.) be two binary operations defined on a non empty set R. Then R is said to form a ring w.r.t addition (+) and multiplication (.) if the following conditions are satisfied:

(R, +) is an abelian group ( i.e commutative group)
(R, .) is a semigroup
For any three elements a, b, c $\epsilon$ R the left distributive law a.(b+c) =a.b + a.c and the right distributive property (b + c).a =b.a + c.a holds.

Therefore a non- empty set R is a ring w.r.t to binary operations + and . if the following conditions are satisfied.

For all a, b $\epsilon$ R, a+b $\epsilon$ R,
For all a, b, c $\epsilon$ R a+(b+c)=(a+b)+c,
There exists an element in R, denoted by 0 such that a+0=a for all a $\epsilon$ R
For every a $\epsilon$ R there exists an y $\epsilon$ R such that a+y=0. y is usually denoted by -a
a+b=b+a for all a, b $\epsilon$ R.
a.b $\epsilon$ R for all a, b $\epsilon$ R.
a.(b.c)=(a.b).c for all a, b, c $\epsilon$ R
For any three elements a, b, c $\epsilon$ R a.(b+c) =a.b + a.c and (b + c).a =b.a + c.a. And the ring is denoted by (R, +, .).

Some Examples –

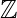( $\mathbb{Z}$ , + ) is a commutative group .( 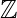$\mathbb{Z}$ , .) is a semi-group. The distributive law also holds. So, (( 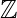$\mathbb{Z}$ , +, .) is a ring.
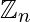Ring of Integers modulo n: For a n $\epsilon$ [Tex]\mathbb{N} [/Tex]let $\mathbb Z_n$ be the classes of residues of integers modulo n. i.e $\mathbb Z_n$ ={ $\bar{0}, \bar{1}, \bar{2}, ......., \overline{n-1}$ ).
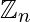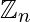( $\mathbb Z_n$ , +) is a commutative group ere + is addition(mod n).
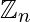( $\mathbb Z_n$ , .) is a semi group here . denotes multiplication (mod n).
Also the distributive laws hold. So ((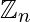 $\mathbb Z_n$ , +, .) is a ring.
The set S = {0, 1, 2, 3, 4} is a ring with respect to operation addition modulo 5 & multiplication modulo 5.

(S,+5) is an Abelian Group. From the above 1st composition table we can conclude that (S,+5) satisfies –

Closure : a ∈ S ,b ∈ S => a +₅ b ∈ S ; ∀ a,b ∈ S
Associativity : (a+₅b)+5c = a+₅(b+₅c) ; ∀ a,b,c ∈ S.
Existence of identity 0 : (a+₅b)+₅c = a+₅(b+₅c) ; ∀ a,b,c ∈ S.
Existence of inverse: Inverse of 0, 1, 2, 3, 4 are 0, 4, 3, 2 , 1 respectively &
Commutative : (a+₅b) = (b+₅a) ; ∀ a,b ∈ S

2. (S,*₅) is an Semi Group. From the above 2nd composition table we can conclude that (S,*₅) satisfies :

Closure : a ∈ S ,b ∈ S => a *₅ b ∈ S ; ∀ a,b ∈ S
Associativity : (a*₅b)*₅c = a*₅(b*₅c) ; ∀ a,b,c ∈ S

3. Multiplication is distributive over addition :

(a) Left Distributive : ∀ a, b, c ∈ S :

a*₅ (b +₅ c)

= [ a * (b + c) ] mod 5

= [a*b + a*c] mod 5

= (a *₅ b) +5 (a *₅ c)

⇒ Multiplication modulo 5 is distributive over addition modulo 5.

Similarly , Right Distributive law can also be proved.

So, we can conclude that (S,+,*) is a Ring.

Many other examples also can be given on rings like (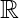 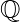$\mathbb R$ , +, .), ( $\mathbb Q$ , +, .) and so on.

Before discussing further on rings, we define Divisor of Zero in A ringand the concept of unit.

Divisor of Zero in A ring –
In a ring R a non-zero element is said to be divisor of zero if there exists a non-zero element b in R such that a.b=0 or a non-zero element c in R such that c.a=0 In the first case a is said to be a left divisor of zero and in the later case a is said to be a right divisor of zero . Obviously if R is a commutative ring then if a is a left divisor of zero then a is a right divisor of zero also .

Example – In the ring (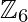 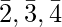$\mathbb Z_6$ , +, .) $\bar{2}, \bar{3}, \bar{4}$ are divisors of zero since
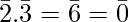$\bar{2}.\bar{3}=\bar{6}=\bar{0}$ and so on .
On the other hand the rings (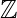 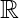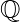$\mathbb Z$ , +, .), ( $\mathbb R$ , +, .), ( $\mathbb Q$ , +, .) contains no divisor of zero .

Units –
In a non trivial ring R( Ring that contains at least to elements) with unity an element a in R is said to be an unit if there exists an element b in R such that a.b=b.a=I, I being the unity in R. b is said to be multiplicative inverse of a.

Some Important results related to Ring:

If R is a non-trivial ring(ring containing at least two elements ) withunity I then I 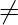$\neq$ 0.
If I be a multiplicative identity in a ring R then I is unique .
If a be a unit in a ring R then its multiplicative inverse is unique .
In a non trivial ring R the zero element has no multiplicative inverse .

Types of Ring :

Null Ring : The singleton set : {0} with 2 binary operations ‘+’ & ‘*” defined by :
0+0 = 0 & 0*0 = 0 is called zero/ null ring.
Ring with Unity : If there exists an element in R denoted by 1 such that :
1*a = a* 1 = a ; ∀ a ∈ R, then the ring is called Ring with Unity.
Commutative Ring : If the multiplication in the ring R is also commutative, then ring is called a commutative ring.
Ring of Integers : The set I of integers with 2 binary operations ‘+’ & ‘*’ is known as ring of Integers.
Boolean Ring : A ring whose every element is idempotent, i.e. , a² = a ; ∀ a ∈ R
Now we introduce a new concept Integral Domain.

Integral Domain – A non -trivial ring(ring containing at least two elements) with unity is said to be an integral domain if it is commutative and contains no divisor of zero ..

Examples –
The rings (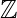 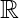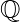$\mathbb Z$ , +, .), ( $\mathbb R$ , +, .), ( $\mathbb Q$ , +, .) are integral domains.
The ring (2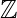 $\mathbb Z$ , +, .) is a commutative ring but it neither contains unity nor divisors of zero. So it is not an integral domain.

Next we will go to Field .

Field – A non-trivial ring R with unity is a field if it is commutative and each non-zero element of R is a unit . Therefore a non-empty set F forms a field .r.t two binary operations + and . if

For all a, b $\epsilon$ F, a+b $\epsilon$ F,
For all a, b, c $\epsilon$ F a+(b+c)=(a+b)+c,
There exists an element in F, denoted by 0 such that a+0=a for all a $\epsilon$ F
For every a $\epsilon$ R there exists an y $\epsilon$ R such that a+y=0. y is usually denoted by (-a)
a+b=b+a for all a, b $\epsilon$ F.
a.b $\epsilon$ F for all a.b $\epsilon$ F.
a.(b.c)=(a.b).c for all a, b $\epsilon$ F
There exists an element I in F, called the identity element such that a.I=a for all a in F
For each non-zero element a in F there exists an element, denoted by 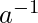$a^{-1}$ in F such that 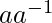$a a^{-1}$ =I.
a.b =b.a for all a, b in F .
a.(b+c) =a.b + a.c for all a, b, c in F

Examples – The rings (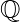 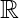$\mathbb Q$ , +, .), ( $\mathbb R$ , + . .) are familiar examples of fields.

Some important results:

A field is an integral domain.
A finite integral domain is a field.
A non trivial finite commutative ring containing no divisor of zero is an integral domain

Last Updated : 16 Feb, 2023