Lines and Angles are the basic terms used in the Geometry. They provide a base for understanding all the concepts of geometry. We define a line as a 1-D figure which can be extended to infinity in opposite directions, whereas an angle is defined as the opening created by joining two or more lines. An angle is measured in degrees or in radians depending on the concept of the problem.
All the geometrical figures have lines and angles and having an understanding of them helps us to better understand the world of Geometry. In this article, we will learn about lines, angles, their types, properties, and others in detail.
Definition of Lines and Angles
We already know that lines and angles are the base shape of geometry and the knowledge of these helps us to better understand the concept of geometry. The basic definition of lines and angles is that the lines are 1-D figures that can be extended infinitely in the opposite direction, whereas an Angle is defined as the degree of mouth open when two lines intersect. If the wide space between the two intersecting lines is more then the angle between them is more.
These concepts are highly used to define various terms and are very helpful for students to study Geometry. Now let’s learn about them in detail.
What are Lines?
Line is defined as a one-dimensional figure that can be extended infinitely. It can extend in both directions and the length of a line is infinite. We can also define a line as the collection of infinitely many points that join together to form a continuous figure.
A line does not have any starting point or an endpoint. If a line has a starting point and a end point then it is called a line segment, whereas if a line only has a starting point but no end point then it is called a ray.
Properties of Lines
Various properties of the lines are,
- If three or more than three points lie in the same line then they are called the collinear points.
- Two lines are called parallel lines if the distance between them is always constant.
- If the line intersects at the right angles then they are called the perpendicular lines.
Types of Lines
We can classify the lines on the basis of their endpoint and the starting point as,
Lines can also be categorized as,
- Parallel Lines
- Perpendicular Lines
- Transversal
Now let’s learn about them in detail.
Line Segment
Line segment is a part of a line that has two endpoints. It is the shortest distance between two points and has a fixed length and can’t be extended further. A line segment AB is shown in the image added below:

Ray
Ray is a line that has a starting point or end point and moves to infinity in one direction. A ray OA is shown in the image added below. Here O is starting point and is moving towards A.

Perpendicular Lines
When two lines form a right angle to each other and meet at a single point then they are called Perpendicular lines. Two perpendicular lines AB and CD are shown in the image added below:

Parallel Lines
Parallel lines are those lines that do not meet each other on a plane at any point and do not intersect with each other. The distance between any two points of the parallel lines is fixed. Two parallel lines l and m are shown in the image added below:

Transversal Lines
When two given lines intersect each other at a distinct point, they will be called transversal lines. Line n is transversal to line l and line m as shown in the image added below:

What are Angles?
When the end points of two rays meet at a common point the figure so formed is called the angle. An angle is measured either in degrees or in radians and we can easily convert a degree to radian. We use ∠ it to represent an angle.
Angles Definition
Types of Angles
There are various types of lines and angles in geometry based on the measurements and different scenarios. Let us learn here all those lines and angles along with their definitions.
- Acute Angle
- Obtuse Angle
- Right Angle
- Straight Angle
- Reflex Angle
- Complete Angle
Acute Angle
When the angle is less than a right angle, then it is called an acute angle. It measures between 0 degrees to 90 degrees. The image added below shows an acute angle:

Obtuse Angle
When the measure of the angle is more than a right angle, then it is called an obtuse angle. It measures greater than 90 degrees. The image added below shows an obtuse angle:

Right Angle
When the angle measures exactly 90 degrees, then it is called a right angle. The image added below shows a right angle:
Straight Angle
If the measure of an angle is 180 degrees then the angle so formed is called the straight angle. The image added below shows a straight angle.
Reflex Angle
When the measurement of the angle is greater than 180° and less than 360° then it is called Reflex Angle. The image added below shows Reflex Angle

Complete Angle
When the measurement of the angle is 360° then it is called Complete Angle. The image added below shows the Complete angle.

We can also categorize angles as,
- Supplementary angles
- Complementary angles
- Adjacent angles
- Vertically opposite angles
Complementary Angles
When two angles sum to 90°, they are called complementary angles. Two complementary angles AOB and BOC are shown in the image below.

Supplementary Angles
When two angles sum up to 180° they will be called Supplementary angles. Two complementary angles PMN and QMN are shown in the image below.

Adjacent Angles
When two angles have a common side and a common vertex and the remaining two sides lie on alternate sides of the common arm then they are called Adjacent Angles. Two adjacent angles A and B are shown in the image below.

Vertically Opposite Angles
When two angles that are opposite two each other and two lines intersect each other at a common point are called vertically opposite angles. Two angles AOB and COD are shown in the image added below.

∠AOD= ∠BOC
∠AOB= ∠DOC
Learn more about, Types of Angles
There are various theorems related to lines and angles, some of these are:
- Vertical Angles are Equal
- Angles in a Triangle Sum Up to 180°
Vertical Angles are Equal
The vertical opposite angles are always equal to each other. The image added below shows the pair of equal vertically opposite angles

We can prove this as,
To Prove:
Proof:
∠MOP+ ∠MON = 180°
∠MOP+ ∠POQ = 180°
Therefore:
∠MOP+ ∠MON = ∠MOP+ ∠POQ
Now subtracting ∠MOP at both sides
∠MOP + ∠MON – ∠MOP = ∠MOP + ∠POQ – ∠MOP
∠MON = ∠POQ
Similarly,
∠MON + ∠NOQ = 180°
∠POQ + ∠NOQ = 180°
Therefore,
∠MOP+ ∠NOQ = ∠POQ+ ∠NOQ
Subtracting ∠NOQ at both sides
∠MOP + ∠NOQ – ∠NOQ = ∠POQ + ∠NOQ – ∠NOQ
∠MOP = ∠POQ
Thus,
Angles in a Triangle Sum Up to 180°
Sum of all the angles in any triangle is 180°. This is proved below, Suppose we have a triangle ABC as shown in the image below:
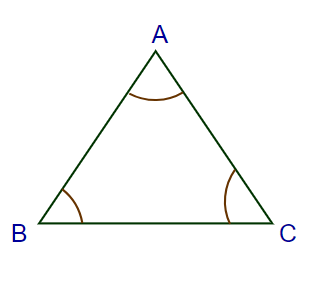
To Prove: ∠A + ∠B + ∠C = 180°
Proof:
Draw a line parallel to BC and pass through vertices A of the triangle.

Now as both lines PQ and BC are parallel, AB and AC are transversal.
So:
- ∠ PAB = ∠ ABC (Alternate Interior Angles)…(i)
- ∠ QAC = ∠ ACB (Alternate Interior Angles)…(ii)
Now, ∠ PAB + ∠ BAC + ∠ QAC = 180° (Linear Pair)…(iii)
From eq (i), (ii) and (iii)
∠ ABC + ∠ BAC + ∠ ACB = 180°
∠A + ∠B + ∠C = 180°
Proved.
Read more about Angle Sum Property of Triangle.
Properties of Lines and Angles
In this section, we will learn about some general properties of lines and angles:
Properties of Lines
There are the following properties of line
- Line has only one dimension i.e. length. It does not have breadth and height.
- A line has infinite points on it.
- Three points lying on a line are called collinear points
Properties of Angles
There are the following properties of angles
- Angles tell about how much a person has rotated from his position.
- Angles are formed when two lines meet and they are called arms of the angle.
Related Articles
Examples on Lines and Angles
Example 1: Find the reflex angle of ∠x, if the value of ∠x is 75 degrees.
Solution:
Let the reflex angle of ∠x be ∠y.
Now, according to the properties of lines and angles, the sum of an angle and its reflex angle is 360°.
Thus,
∠x + ∠y = 360°
75° + ∠y = 360°
∠y = 360° − 75°
∠y = 285°
Thus, the reflex angle of 75° is 285°.
Example 2: Find the complementary angle of ∠x, if the value of ∠x is 75 degrees.
Solution:
Let the complementary angle of ∠x be ∠y.
Now, according to the properties of lines and angles, the sum of an angle and its complementary angle is 90°.
Thus,
∠x + ∠y = 90°
75° + ∠y = 90°
∠y = 90° − 75°
∠y = 15°
Thus, the complementary angle of 75° is 15°.
Example 3: Find the supplementary angle of ∠x, if the value of ∠x is 75 degrees.
Solution:
Let the supplementary angle of ∠x be ∠y.
Now, according to the properties of lines and angles, the sum of an angle and its supplementary angle is 180°.
Thus,
∠x + ∠y = 180°
75° + ∠y = 180°
∠y = 180° − 75°
∠y = 105°
Thus, the supplementary angle of 75° is 105°.
Example 4: Find the value of ∠A and ∠B if ∠A = 4x and ∠B = 6x are adjacent angles and they form a straight line.
Solution:
According to the properties of lines and angles, the sum of the adjacent linear angles formed by a line is 180°.
Thus,
∠A + ∠B = 180°
4x + 6x = 180°
10x = 180°
x = 180°/10 = 18°
Thus,
- ∠A = 4x = 4×18 = 72°
- ∠B = 6x = 6×18 = 108°
FAQs on Lines and Angles
What are Lines in Geometry?
We define a line in geometry as a one-dimensional figure that extends infinitely in opposite directions. A line can be vertical or horizontal with respect to the reference line or plane. As the line can extend infinitely the length of the line is infinity.
What are Angles in Geometry?
An angle in geometry is defined as the shape formed when two lines meet one another at some point. We measure in degrees and radians. The symbol ∠ is used to represent the radian.
What are the types of Angles?
There are five types of angles that are,
- Acute Angle
- Right Angle
- Obtuse Angle
- Straight Angle
- Reflex Angle
What are the types of Lines?
The different types of lines are:
- Horizontal lines
- Vertical lines
- Parallel lines
- Perpendicular lines
What are the Properties of Lines and Angles?
Various properties of the lines and angles are,
- Two parallel lines never meet each other.
- The distance between two parallel lines is always equal.
- For intersecting lines vertical opposite angles are always equal, etc.
Share your thoughts in the comments
Please Login to comment...