When two lines share a common endpoint, called Vertex then an angle is formed between these two lines is known as the pair of angles. Below is the pictorial representation of the pair of angles.
Some of the pair of angles we saw is below:
- Complementary Angles
- Supplementary Angles
- Adjacent Angles
- Linear Pair of Angles
- Vertical Angles
Complementary Angles
When we have two angles whose addition equals 90° then the angles are called Complementary Angles.
Example:
50° and 40° (50° + 40° = 90°)
70° and 20° (70° + 20° = 90°)
Below is the pictorial representation of the Complementary Angles.
- If we have two angles as x° and y° and x° + y° = 90° then x is called the complementary angle of y and y is called the complementary angle of x.
Example: We have 20° and 70° then, 20° is a complementary angle of 70° and 70° is a complementary angle of 20°.
- If we have one angle as x° then to find a complementary angle we need to subtract it from 90°.
Example: We have 30° then the complementary angle of it is 90° – 30° which is 60°
Supplementary Angles
When we have two angles whose addition equals to 180° then the angles are called Supplementary Angles.
Example:
150° and 30° (150° + 30° = 180°)
70° and 110° (70° + 110° = 180°)
Below is the pictorial representation of the Supplementary Angle.
- If we have two angles as x° and y° and x° + y° = 180° then x is called the supplementary angle of y and y is called the supplementary angle of x.
Example: We have 100° and 80° then, 100° is the supplementary angle of 80° and 80° supplementary angle of 100°.
- If we have one angle as x° then to find a supplementary angle we need to subtract it from 180°.
Example: We have 60° then the supplementary angle of it is 180° – 60° which is 120°
Difference Between Complementary Angle and Supplementary Angle
Complementary Angle | Supplementary Angle |
|---|
| Sum of both the angle equals to 90°. | Sum of both the angle equals to 180°. |
| Both the angles are called complements of each other. | Both the angles are called supplement of each other. |
| If one angle is x°, its complement is 90° – x°. | If one angle is x°, its supplement is 180° – x°. |
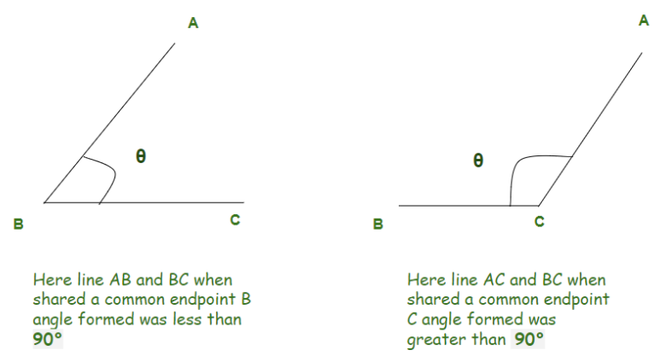
Adjacent Angles
When we have two angles with a common side, a common vertex without any overlap we call them Adjacent Angles.
We know what conditions two angles need to fulfill to be Adjacent angles. Let’s see some of the examples where we might get confused that whether they are adjacent angles or not.
Here θ1 and θ2 are having a common vertex, they don’t overlap but because they don’t share any common side they aren’t Adjacent Angles.
Here θ1 and θ2 are having a common vertex, they share a common side but they overlap so they aren’t Adjacent Angles.
Linear Pair of Angles
We say two angles as linear pairs of angles if both the angles are adjacent angles with an additional condition that their non-common side makes a Straight Line.
Let’s see some examples for a better understanding of Pair of Angles.
Example 1:
Let’s call the intersection of line AC and BD to be O. Now we see four angles are there let’s try to observe them one by one.
- θ1 and θ2 are adjacent angles and their non-common sides are AO and OC, AO + OC = AC is a Straight Line so both are linear pairs of angles.
- θ2 and θ3 are adjacent angles and their non-common sides are BO and OD, BO + OD = BD is a Straight Line so both are linear pairs of angles.
- θ3 and θ4 are adjacent angles and their non-common sides are CO and OA, CO + OA = CA is a Straight Line so both are linear pairs of angles.
- θ4 and θ1 are adjacent angles and their non-common sides are D0 and OB, DO + OB = DB is a Straight Line so both are linear pair of angles.
Vertical Angles
A vertical angle is a pair of non-adjacent angles that are formed by the intersection of two Straight Lines.
Here we see line AD and line BC intersect at one point let’s call it X and thus four angles are formed
∠AXB = θ1
∠BXD = θ2
∠DXC = θ3
∠CXA = θ4
θ1 and θ2 are non-adjacent angles and formed by the intersection of line AD and BC therefore they are Vertical Angles are always Equal so θ1 = θ2. Similarly, θ3 and θ4 are also vertical angles therefore θ3 = θ4. Let’s try to understand with a question:
Here we see ∠BXD and b are vertically opposite angles therefore
b = ∠BXD
b = 60°
and we also see that ∠DXC and a are vertically opposite angles therefore
a = ∠DXC
a = 120°