Class 9 RD Sharma Solutions – Chapter 8 Introduction to Lines and Angles- Exercise 8.2 | Set 1
Last Updated :
30 Apr, 2021
Question 1: In the below Fig. OA and OB are opposite rays:
(i) If x = 25°, what is the value of y?
(ii) If y = 35°, what is the value of x?

Solution:
(i) Given:
x = 25
In the figure;
∠AOC and ∠BOC are forming a linear pair
So, ∠AOC + ∠BOC = 180°
In the figure;
∠AOC = 2y + 5 and ∠BOC = 3x
∠AOC + ∠BOC = 180°
(2y + 5) + 3x = 180
(2y + 5) + 3 (25) = 180
2y + 5 + 75 = 180
2y + 80 = 180
2y = 100
y =  = 50
= 50
Hence,
y = 50°
(ii) Given:
y = 35°
In the figure;
∠AOC + ∠BOC = 180° {Linear pair angles}
(2y + 5) + 3x = 180
(2(35) + 5) + 3x = 180
75 + 3x = 180
3x = 105
x = 35
Therefore, x = 35°
Question 2. In the below figure, write all pairs of adjacent angles and all the linear pairs.

Solution:
In the figure;
Pairs of adjacent angles are:
(∠AOC, ∠COB);
(∠AOD, ∠BOD);
(∠AOD, ∠COD);
(∠BOC, ∠COD)
∠AOD + ∠BOD = 180° {Linear pair}
and
∠AOC+ ∠BOC = 180° {Linear pair}
Question 3. In the given figure, find x. Further find ∠BOC, ∠COD, and ∠AOD.

Solution:
In the figure;
∠AOD and ∠BOD are forming linear pair,
Thus,
∠AOD+ ∠BOD = 180°
And,
∠AOD + ∠BOC + ∠COD = 180°
Given:
∠AOD = (x+10)°,
∠COD = x°
and
∠BOC = (x + 20)°
(x + 10) + x + (x + 20) = 180°
3x + 30 = 180°
3x = 180 – 30
x = 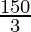
x = 50°
Here,
∠AOD = (x+10) = 50 + 10 = 60
∠COD = x = 50°
∠BOC = (x+20) = 50 + 20 = 70°
Therefore,
∠AOD = 60°,
∠COD = 50°
and
∠BOC=70°
Question 4. In figure, rays OA, OB, OC, OD, and OE have the common endpoint 0. Show that ∠AOB+∠BOC+∠COD+∠DOE+∠EOA=360°.

Solution:
Given:
Rays OA, OB, OC, OD and OE have the common endpoint O.
Construct: Draw an opposite ray OX to ray OA, which make a straight line AX.

In the figure:
∠AOB + ∠BOX = 180° {Linear pair}
Or,
∠AOB + ∠BOC + ∠COX = 180° ……….(i)
Also,
∠AOE + ∠EOX = 180° {Linear pair}
Or,
∠AOE + ∠DOE + ∠DOX = 180° ………..(ii)
After adding equations, (i) and (ii), we will get;
∠AOB + ∠BOC + ∠COX + ∠AOE + ∠DOE + ∠DOX = 180° + 180°
∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°
Hence, Proved.
Question 5. In figure, ∠AOC and ∠BOC form a linear pair. If a – 2b = 30°, find a and b?

Solution:
Given:
∠AOC and ∠BOC are forming a linear pair.
a + b = 180° …….(i)
a – 2b = 30° …….(ii) {given}
After subtracting equation (ii) from (i), we will get
a + b – a + 2b = 180 – 30
3b = 150
b = 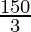
b = 50°
Thus,
a – 2b = 30°
a – 2(50) = 30°
a = 30 + 100
a = 130°
Hence,
a = 130°
b = 50°
Question 6. How many pairs of adjacent angles are formed when two lines intersect at a point?
Solution:
Here, the four pairs of adjacent angles are formed when two lines intersect each other at a single point.
So here Let two lines AB and CD intersect at point O as shown below in the figure

Thus, the 4 pair of adjacent angles are :
(∠AOD, ∠DOB),
(∠DOB, ∠BOC),
(∠COA, ∠AOD)
and
(∠BOC, ∠COA)
Question 7. How many pairs of adjacent angles, in all, can you name in the figure given?

Solution:
The number of Pairs of adjacent angles, from the following figure are;
∠EOC and ∠DOC
∠EOD and ∠DOB
∠DOC and ∠COB
∠EOD and ∠DOA
∠DOC and ∠COA
∠BOC and ∠BOA
∠BOA and ∠BOD
∠BOA and ∠BOE
∠EOC and ∠COA
∠EOC and ∠COB
Thus, we have 10 pairs of adjacent angles.
Question 8. In figure, determine the value of x.

Solution:
As we know that, the sum of all the angles around a point O is equal to 360°.
Thus,
3x + 3x + 150 + x = 360°
7x = 360° – 150°
7x = 210°
x = 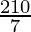
x = 30°
Hence, the value of x is 30°.
Question 9. In figure, AOC is a line, find x.

Solution:
In the following figure,
∠AOB + ∠BOC = 180° {Linear pairs}
70 + 2x = 180
2x = 180 – 70
2x = 110
x = 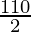
x = 55°
Hence, the value of x is 55°.
Question 10. In figure, POS is a line, find x.

Solution:
In the following figure;
∠POQ + ∠QOS = 180° {Linear pair}
∠POQ + ∠QOR +∠SOR = 180°
60° + 4x + 40° = 180°
4x = 180° -100°
4x = 80°
x = 20°
Thus, the value of x is 20°.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...