Squares and Square roots are highly used mathematical concepts which are used for various purposes. Squares are numbers produced by multiplying a number by itself. Conversely, the square root of a number is the value that, when multiplied by itself, results in the original number. Thus, squaring and taking the square root are inverse operations.
This can be understood with the help of an example such as take q number 3 then its square is 32 = 9. Now the square root of 9 is √(9) = 3. Thus, it is evident that the square root is the inverse operation of the square.
Let’s learn more about square and square roots in this article including properties of square numbers, squares of different types of numbers, properties of square roots, etc.
What is a Square of a Number?
The square of a Number is defined as the product of the number by itself, i.e. when a number is multiplied by itself then the number obtained is called the square of the original number. For example, the square of the first 10 natural numbers is,
Square and Square Roots Table
| Number | Square | Number | Square |
|---|
| (1)2 | 1 | (6)2 | 36 |
| (2)2 | 4 | (7)2 | 49 |
| (3)2 | 9 | (8)2 | 64 |
| (4)2 | 16 | (9)2 | 81 |
| (5)2 | 25 | (10)2 | 100 |
The square of any real number is used to find the area of a square and other things.
Representation of Square
A square is represented with the number 2 represented as the exponent on the number i.e. x2. For example, the square of 3 is written as 32, similarly, the square of 7 is written as 72, and so on.
Note: The square of all the real numbers is always positive.
Squares of Negative Numbers
The squares of negative numbers also result in a positive value, as we know that the multiplication of two negative values always yields a positive value i.e.,
Thus, the square of the negative number is always positive i.e., (-n)2 = (-n) × (-n) = n2 (positive number)
For example, the square of (-5) is (-5)2 = (-5) × (-5) = 25.
Square of 2
As already discussed, the square can be found for any number by multiplying the number by itself. Thus, the square of 2 is 2×2 = 4.
Properties of Square Numbers
Square of the number is a number that is obtained by multiplying the number by itself. Various properties of the square of are,
- A square of 0 is 0 and a square of 1 is 1.
- Squares of even numbers are always even numbers and squares of odd numbers are always odd.
- Square of any real number is always a positive number.
- Square of the imaginary number can be negative.
- None of the square numbers ends with 2, 3, 7, or 8 at the unit’s place.
- A number ending in an odd number of zeros is never a perfect square.
- Square of the square root of any number is equal to the number itself. For example (√5)2 = 5.
Square Numbers 1 to 30
The square of numbers from 1 to 30 i.e the square of the first 30 natural numbers is given in the image discussed below,
| Number | Square | Number | Square | Number | Square |
|---|
| 1 | 1 | 11 | 121 | 21 | 441 |
| 2 | 4 | 12 | 144 | 22 | 484 |
| 3 | 9 | 13 | 169 | 23 | 529 |
| 4 | 16 | 14 | 196 | 24 | 576 |
| 5 | 25 | 15 | 225 | 25 | 625 |
| 6 | 36 | 16 | 256 | 26 | 676 |
| 7 | 49 | 17 | 289 | 27 | 729 |
| 8 | 64 | 18 | 324 | 28 | 784 |
| 9 | 81 | 19 | 361 | 29 | 841 |
| 10 | 100 | 20 | 400 | 30 | 900 |
Numbers Between Squares
There is a way to calculate the number between the square of two consecutive numbers. Let’s take two consecutive numbers n and n+1 then the number between their squares is given by the formula 2n.
Proof:
Take two numbers n and n+1,
Their squares are (n)2 and (n+1)2 respectively.
Numbers between these squares = (n+1)2 – (n)2 -1
= n2 + 1 + 2n – n2 -1
= 2n
For example, find the number between (2)2 and (3)2
Solution:
Given numbers are,
(2)2 and (3)2 = (2)2 and (2+1)2
Thus, n = 2
Number between (2)2 and (3)2 = 2×2 = 4
What are Square Roots?
Square roots are nothing but the inverse operation of the square i.e. if a is the square of b then, the square root of b is a. As such,
If, a2 = b
Then, √(b) = a
The square root of any number is both positive and negative i.e. √(b) = ±a. This is because the square of (a)2 = b and (-a)2 = b, so its square is both positive and negative.
For example,
- √4 = ±2
- √9 = ±3
- √16 = ±4
- √25 = ±5
Representation of Square Root
The square root is represented with the symbol √ called radical or radix followed by the number which is called radicand i.e., √x. The image given below shows the square root symbol.
.png)
Properties of Square Root
Various properties of the Square Root of any number are,
- If the unit digit of a number is 2,3,7 or 8, then it does not have a root in N (the set of natural numbers).
- If a number ends in an odd number of zeros, then it does not have a square root. If a square number is followed by an even number of zeros, it has a square root in which the number of zeros, in the end, is half the number of zeros in the number.
- The square root of an even square number is even and the root of an odd square number is odd.
Square Roots of Perfect Squares
Perfect squares are those numbers whose square roots yields whole number i.e. their square root always results in number such as 3, 4, 1, 11, etc.
Some square roots of the perfect square are given in the table below,
| Perfect Square | Square Root |
|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
Square Root of Imperfect Squares
Imperfect squares are those numbers whose square roots yield any rational number except whole numbers i.e. their square root always results in numbers such as 3.34, 4/7, 1.111112113…, 1.732, etc.
Some square roots of the imperfect square are given in the table below,
| Imperfect Square | Square Root |
|---|
| 2 | 1.414 |
| 3 | 1.732 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.6457 |
| 8 | 2.8284 |
| 10 | 3.1622 |
Square Root of Numbers 1 to 30
The square root of numbers from 1 to 30 is discussed in the image below,
.jpg)
Square Roots 1 to 50 – Table
Number
| Square Root
| Number
| Square Root
| Number
| Square root
|
|---|
|
√1
|
1
|
√18
|
4.2426
|
√35
|
5.9161
|
|
√2
|
1.4142
|
√19
|
4.3589
|
√36
|
6
|
|
√3
|
1.7321
|
√20
|
4.4721
|
√37
|
6.0828
|
|
√4
|
2
|
√21
|
4.5826
|
√38
|
6.1644
|
|
√5
|
2.2361
|
√22
|
4.6904
|
√39
|
6.2450
|
|
√6
|
2.4495
|
√23
|
4.7958
|
√40
|
6.3246
|
|
√7
|
2.6458
|
√24
|
4.8990
|
√41
|
6.4031
|
|
√8
|
2.8284
|
√25
|
5
|
√42
|
6.4807
|
|
√9
|
3
|
√26
|
5.0990
|
√43
|
6.5574
|
|
√10
|
3.1623
|
√27
|
5.1962
|
√44
|
6.6332
|
|
√11
|
3.3166
|
√28
|
5.2915
|
√45
|
6.7082
|
|
√12
|
3.4641
|
√29
|
5.3852
|
√46
|
6.7823
|
|
√13
|
3.6056
|
√30
|
5.4772
|
√47
|
6.8557
|
|
√14
|
3.7417
|
√31
|
5.5678
|
√48
|
6.9282
|
|
√15
|
3.8730
|
√32
|
5.6569
|
√49
|
7
|
|
√16
|
4
|
√33
|
5.7446
|
√50
|
7.0711
|
|
√17
|
4.1231
|
√34
|
5.8310
|
|
|
Finding Square Roots
We can find square roots through the prime factorization of a number. Let’s look at some examples:
| Prime Factorization of a Number | Prime Factorization of its square |
|---|
| 6 = 2 × 3 | 36 = 2 × 2 × 3 × 3 |
| 12 = 2 × 2 × 3 | 144 = 2 × 2 × 2 × 2 × 3 × 3 |
| 15 = 5 × 3 | 225 = 5 × 5 × 3 × 3 |
We can see that in the prime factorization of its square, each prime number occurs twice as compared to the prime factorization of the number itself. By pairing the prime factors, we can get a square root.
Finding the square root of decimal numbers
There are several methods of finding the square root of decimal numbers and the most famous and easiest method of manually finding the square root is called the Prime Factorization Method. For large numbers, we go for Long Division Method since the former method becomes tedious in the case of very large numbers.
Interesting Patterns in Square Roots and Squares
There are interesting patterns in the square roots and squares of the numbers, some of these patterns are as follows:
Adding Triangular Numbers
Triangular numbers are numbers whose dot patterns can be arranged as triangles. For example:

If we combine two consecutive triangle numbers, we can get a number that is a square.
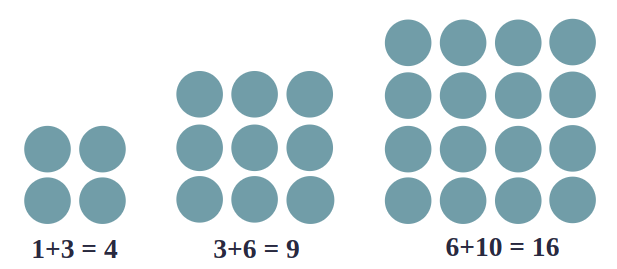
Squares of 1, 11, 111, 1111…
Squares of these numbers give rise to a beautiful pattern.
(1)2 = 1
(11)2 = 1 2 1
(111)2 = 1 2 3 2 1
(1111)2 = 1 2 3 4 3 2 1
(11111)2 = 1 2 3 4 5 4 3 2 1
Squares of Numbers with 5 as a Unit Digit
Let’s assume a number with unit digit 5, i.e.
a52 = (10a + 5)2
= 10a(10a + 5) + 5(10a + 5)
= 100a + 50a + 50a + 25
= 100a (a + 1) + 25
Example:
252 = 625 = (2 × 3) hundreds + 25
352 = 1225 = (3 × 4) hundreds + 25
752 = 5625 = (7 × 8) hundreds + 25
1252 = 15625 = (12 × 13) hundreds + 25
People Also Read:
Squares and Square Roots Examples
Example 1: Find the square of 23.
Solution:
232 = (20 + 3)2
= 20(20 + 3) + 3(20 +3)
= 202 + 20 × 3 + 3 × 20 + 32
= 400 + 60 + 60 + 9
= 529
Example 2: Find the square of 39.
Solution:
392 = (30 + 9)2
⇒ 392 = 30 (30 + 9) + 9 (30 + 9)
⇒ 392 = 302 + 30 × 9 + 9 × 30 + 92
⇒ 392 = 900 + 270 + 270 + 81
⇒ 392 = 1521
Example 3: Find the square root of 144.
Solution:
144 = (2 × 2) × (2 × 2) × (3 × 3)
⇒ 144 = 22 × 22 × 32
⇒ 144 = (2 × 2 × 3)2
⇒ 144 = 122
Therefore, √144 = 12
Sometimes a number is not a perfect square.
Example 4: Is 2352 a perfect square? If not, find the smallest multiple of 2352 which is a perfect square. Find the square root of the new number.
Solution:
2352 = 2 × 2 × 2 × 2 × 3 × 7 × 7
⇒ 2352 = 24 × 3 × 72
As the prime factor 3 has no pair, 2352 is not a perfect square.
If 3 gets a pair then the number will become perfect square.
2352 = 2 × 2 × 2 × 2 × 3 × 7 × 7
⇒ 2352 = 24 × 32 × 72
⇒ 2352 = 22 × 3 × 7 = 84
Example 5: Square root of 19.36
Solution:
Step 1: Make pairs of an integral part and decimal part of the number. Add a zero to the extreme right of the decimal part if required.

Step 2: Find the perfect square of an integral part, find the number closest to the integral part (Either small or equal). In this case, the square of 4 is 16 which is closest to 19:

Step 3: Put the decimal Part next to the Remainder obtained. Double the divisor of an Integral Part and place it in the next divisor, now we have to find the unit place value of this number.

Step 4: Now we have to find the unit place’s number which should be multiplied in order to get 336, here we can see, if we multiply 84 with 4, we will get 336.

Hence, we obtained 4.4 as the square root of 19.36
Square and Square Roots Class 8
In Class 8 mathematics, students are introduced to the concepts of squares and square roots, which are fundamental operations in algebra. This topic helps build a foundational understanding of how numbers interact in specific arithmetic operations.
Applications of Square and Square Roots
- Understanding squares and square roots helps in solving various algebraic and geometric problems, like finding the area of squares or solving quadratic equations.
- It encourages students to think critically when tackling problems that require manipulation of squares and square roots.
- Knowledge of these concepts is useful in real-world scenarios, such as calculating areas and understanding patterns in numbers.
FAQs on Squares and Square Roots
What are Squares and Square Roots?
A number when multiplied by itself produces a square i.e. square of any number is defined as the multiplication of the number itself. Square roots are defined as the inverse operation of the square. For example, if the square of ‘a’ (a2) is ‘b’ then the square root of ‘b’ is ‘a’ i.e.,
if a2 = b then √(b) = a
How to find the Square Root?
The square root of any number is calculated using
- Prime Factorization Method
- Long Division Method
What are Perfect Squares?
If the square root of a number gives a whole number then it is called a perfect square. For example, 4 is a perfect square, because its root is a whole number (2), i.e.√4 = 2.
What are Imperfect Squares?
If the square root of a number gives a fraction value or decimal value then it is called a imperfect square. For example, √3 is an imperfect square, because its root is an irrational number (1.732…), i.e.√3 = 1.732…
What is the difference between squares and square roots?
The main difference between the square and square root of the number is, the square of a number is found by multiplying the number by itself whereas the square root is the inverse operation of the square.
What are examples of imperfect squares?
Some examples of imperfect squares are, √(10) = 3.16227, √(20) = 4.472135, etc.
What are examples of perfect squares?
Some examples of perfect squares are, 100 i.e., √(100) = 10, 16 i.e., √(16) = 4, 25 i.e., √(25) = 5, etc.
What is the square of 25?
Square of 25 is 625 i.e., 25×25 = 625.
What is the square of 13?
Square of 13 is 169 i.e., 13×13 = 169.
What is the square of 15?
Square of 15 is 225 i.e., 15×15 = 225.
What is Square Root in Math?
Square root of a number is a number that when multiplied by itself gives the actual number. For example, 2 is the square root of 4
Share your thoughts in the comments
Please Login to comment...